Содержание
- 2. Тайны планетных орбит. Древнегреческие учёные умели решать немногие задачи кинематики – рассчитать либо равномерное прямолинейное движение,
- 3. В конце 17 века Исаак Ньютон открыл законы динамики, сформулировал закон всемирного тяготения и развил математические
- 4. Он также развил новое исчисление, которое оказалось по сути дела тождественным построенному Ньютоном. Обозначения, введённые Лейбницем,
- 5. Дифференциальные исчисления – раздел математики, в котором изучаются производные и их применения к исследованию функции.
- 6. 1). f(x) = 5x + 3 Найти : f(2) f(a) f(a+2) f(a+2) – f(a)
- 7. Приращение функции и аргумента Δх = х – хо – приращение аргумента Δf(х) = f(х) –
- 8. Calculis differentialis – исчисление разностей
- 9. Пусть точка движется вдоль прямой и за время t от начала движения проходит путь s(t). Рассмотрим
- 10. Пусть функция f(x) определена на некотором промежутке, х – точка этого промежутка и число h≠ 0
- 11. Исаак Ньютон (1643 – 1727) «Когда величина является максимальной или минимальной, в этот момент она не
- 12. у = kх + в у(хо) = kхо + в, у(хо + ∆х) = k ∙
- 13. у = х2 у(хо) = хо2, у(хо + ∆х) = (хо + ∆х)2= хо2 + 2
- 15. Скачать презентацию




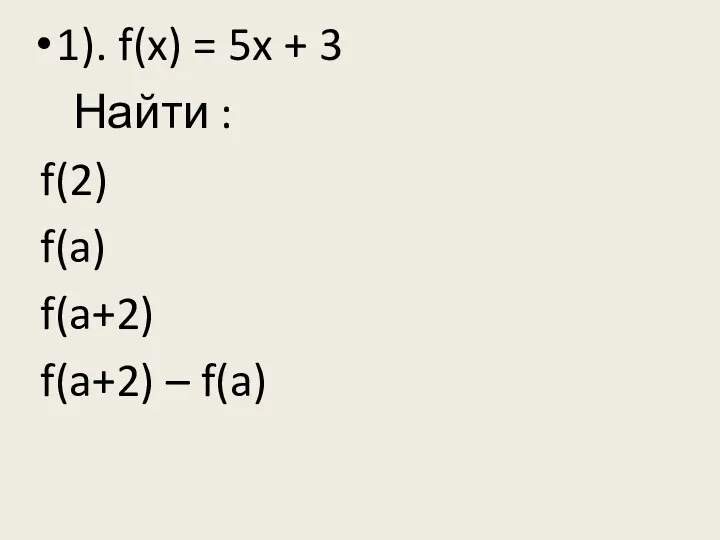





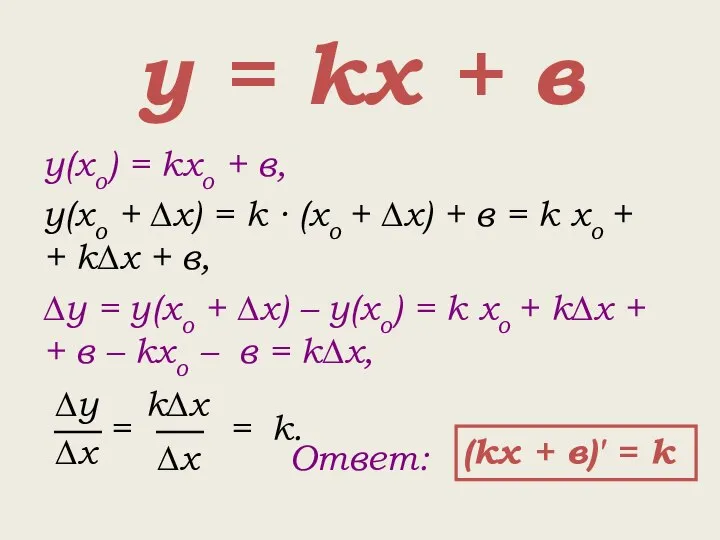
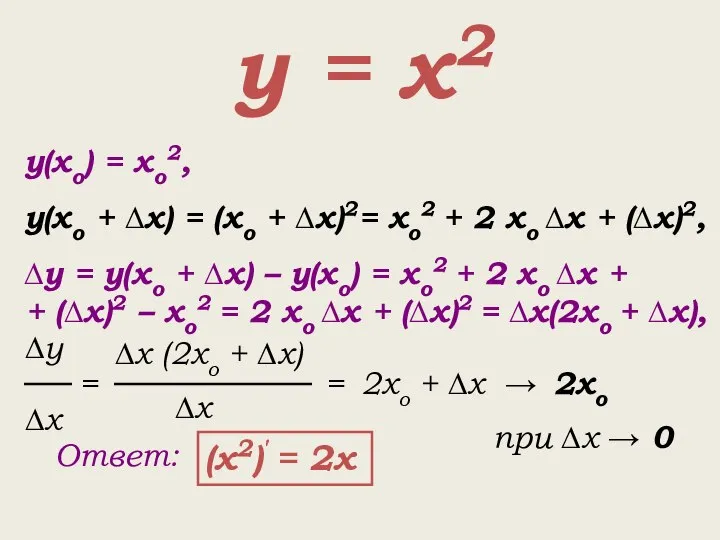
 Презентация по математике "Решение задач на разностное и кратное сравнение чисел" -
Презентация по математике "Решение задач на разностное и кратное сравнение чисел" -  Игра - тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра - тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Презентация на тему Решение уравнений высших степеней
Презентация на тему Решение уравнений высших степеней  Метод подобия треугольников при решении задач
Метод подобия треугольников при решении задач Векторные задачи 1-го типа
Векторные задачи 1-го типа Matrix Algebra аnd Simultaneous Linear Equations. Lecture 10
Matrix Algebra аnd Simultaneous Linear Equations. Lecture 10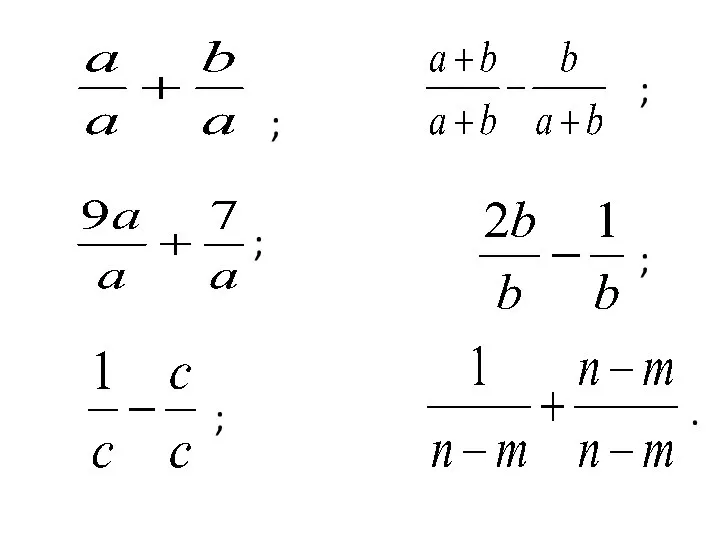 Действия с дробями
Действия с дробями Многогранники и круглые тела в мировой архитектуре
Многогранники и круглые тела в мировой архитектуре Презентация на тему Умножение числа 2
Презентация на тему Умножение числа 2  Обыкновенная дробь
Обыкновенная дробь Умножение обыкновенных дробей
Умножение обыкновенных дробей Декартова система координат
Декартова система координат Переместительное свойство сложения
Переместительное свойство сложения Формулы сокращенного умножения. Подготовка к СОР
Формулы сокращенного умножения. Подготовка к СОР Свойства натурального ряда чисел
Свойства натурального ряда чисел Обратные матрицы
Обратные матрицы Теорема о площади треугольников
Теорема о площади треугольников Презентация на тему Законы алгебры логики
Презентация на тему Законы алгебры логики  Координатная плоскость. 6 класс
Координатная плоскость. 6 класс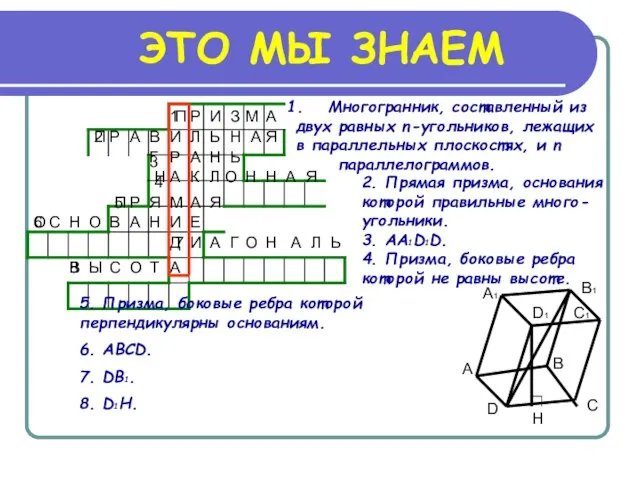 Пирамида. История
Пирамида. История Контрольная работа. Геометрия
Контрольная работа. Геометрия Параллельные плоскости
Параллельные плоскости Pakāpes vingrinājumi (bez atb)
Pakāpes vingrinājumi (bez atb) Координатная плоскость. Математика 6 класс
Координатная плоскость. Математика 6 класс Презентация на тему Прямоугольник
Презентация на тему Прямоугольник  Презентация на тему Треугольники (5 класс)
Презентация на тему Треугольники (5 класс)  algebr_drobi рабочая презентация начиная с 5 ссентября
algebr_drobi рабочая презентация начиная с 5 ссентября Аттестационная работа. Методическая разработка урока Единицы площади. Квадратный метр. 3 класс
Аттестационная работа. Методическая разработка урока Единицы площади. Квадратный метр. 3 класс