Содержание
- 2. Алгеброй называется множество объектов с заданной на нем совокупностью операций, замкнутых относительно этого множества, называемого основным
- 3. Классификация операций: теоретико-множественные операции; специальные операции.
- 4. Теоретико-множественные операции реляционной алгебры
- 5. Операции объединения, пересечения и вычитания требуют от операндов совместимости по типу.
- 6. Два отношения совместимы по типу, если каждое из них имеет одно и то же множество имен
- 7. Объединение отношений называется отношение, содержащее множество кортежей, принадлежащих либо первому, либо второму исходным отношениям, либо обоим
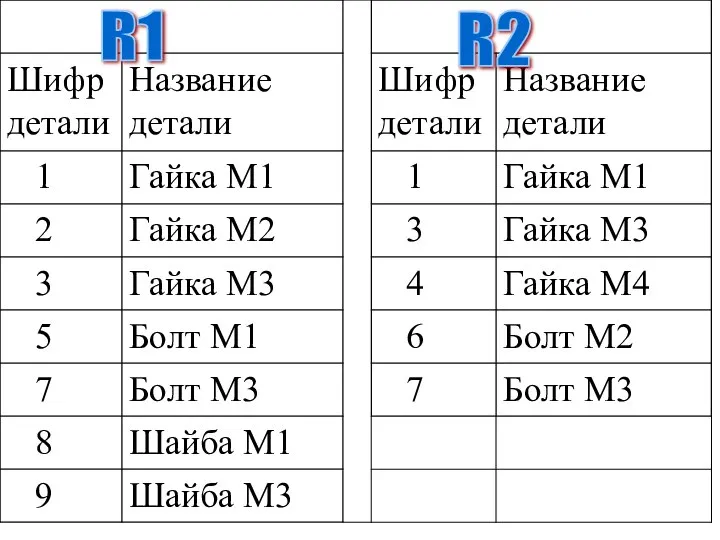
- 8. Пусть заданы два отношения R1 = {r1}, R2 = {r2}, где r1 и r2 — соответственно
- 9. Тогда объединение этих отношений R3=R1 U R2 = {r | r Є r1 U r Є
- 10. R1 R2
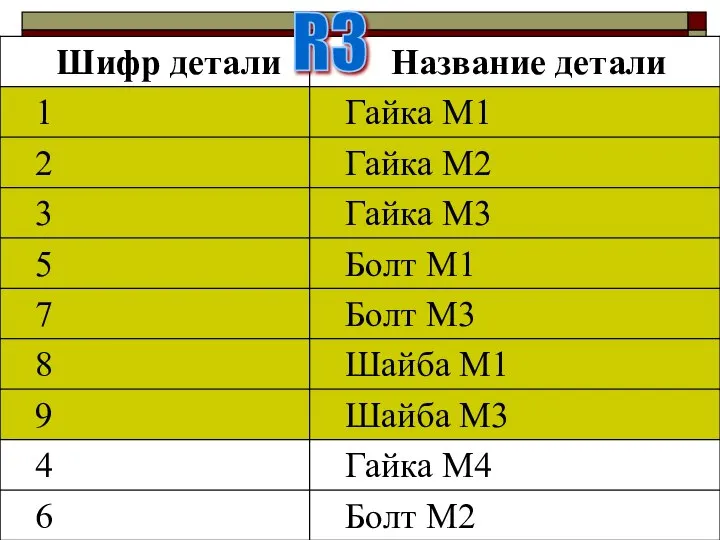
- 11. Перечень деталей, изготавливаемых в цехе R3=R1 U R2
- 12. R3
- 13. Пересечением отношений называется отношение, которое содержит множество кортежей, принадлежащих одновременно и первому и второму отношениям.
- 14. R4 = R1 ∩ R2 = {r | r∈ R1 ∩ r ∈ R2} здесь ∩
- 15. Перечень деталей, которые выпускаются одновременно и на первом и на втором участках цеха.
- 16. R4
- 17. Разностью отношений R1 и R2 называется отношение, содержащее множество кортежей, принадлежащих R1 и не принадлежащих R2.
- 18. R5 = R1 \ R2 = {r | r ∈ R1 ∩ r ∉ R2} R6
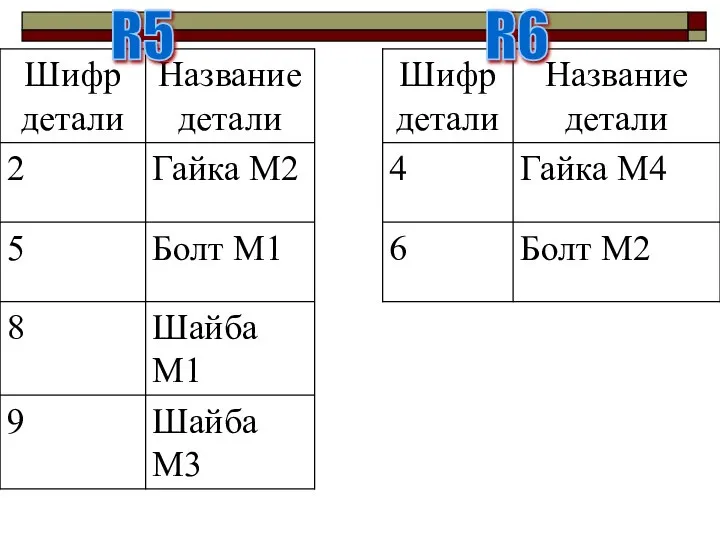
- 19. Пример Отношение R5 содержит перечень деталей, изготавливаемых только на участке 1, отношение R6 содержит перечень деталей,
- 20. R6 R5
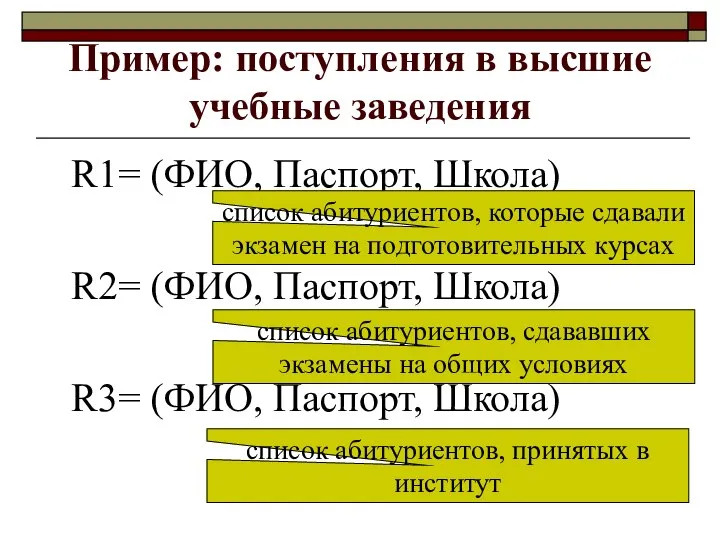
- 21. Пример: поступления в высшие учебные заведения R1= (ФИО, Паспорт, Школа) R2= (ФИО, Паспорт, Школа) R3= (ФИО,
- 22. Ответьте на вопросы: 1. Список абитуриентов, которые поступали два раза и не поступили в ВУЗ. R=R1
- 23. 2. Список абитуриентов, которые поступили в ВУЗ с первого раза, то есть они сдавали экзамены только
- 24. 3. Список абитуриентов, которые поступили в вуз только со второго раза.
- 26. Скачать презентацию














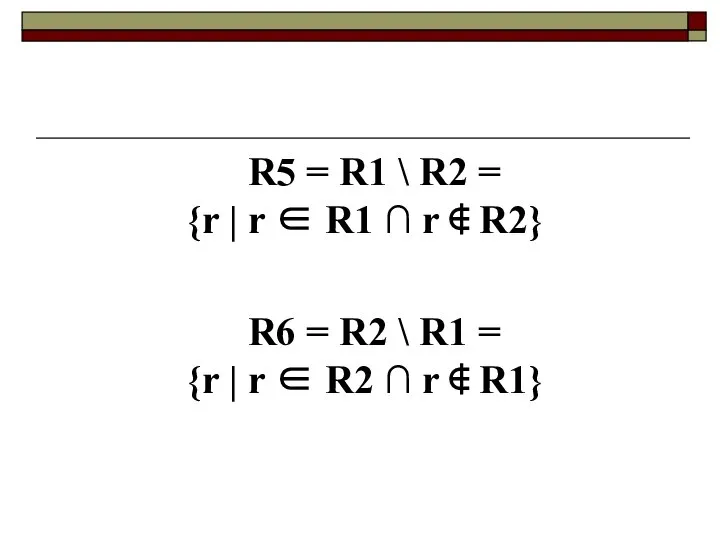




 Решение простейших логарифмических уравнений
Решение простейших логарифмических уравнений Освоение основных универсальных предметных знаний и умений в курсе технологии
Освоение основных универсальных предметных знаний и умений в курсе технологии Сочетательное свойство умножения
Сочетательное свойство умножения Просто, сложно, интересно. Учебный курс предпрофильной подготовки для учащихся 9-х классов
Просто, сложно, интересно. Учебный курс предпрофильной подготовки для учащихся 9-х классов Примеры +7, +8, +9
Примеры +7, +8, +9 Математические ребусы. 6 класс
Математические ребусы. 6 класс Решение уравнений
Решение уравнений Интервальное оценивание
Интервальное оценивание Презентация
Презентация Презентация на тему Математический калейдоскоп
Презентация на тему Математический калейдоскоп  Веселая математика!
Веселая математика! Окружность и круг
Окружность и круг Ряды. Сходимость рядов
Ряды. Сходимость рядов Міри маси, часу, довжини
Міри маси, часу, довжини Решение уравнений и неравенств. Линейные уравнения и неравенства
Решение уравнений и неравенств. Линейные уравнения и неравенства Презентация на тему Системы уравнений
Презентация на тему Системы уравнений  Целые числа. Рациональные числа
Целые числа. Рациональные числа Умножение вида 320 * 3. Решение задач. Устный счёт
Умножение вида 320 * 3. Решение задач. Устный счёт Веб – квест для учащихся 11 класса. Задачи по теме Производная
Веб – квест для учащихся 11 класса. Задачи по теме Производная Параллельные прямые
Параллельные прямые Умножение, деление, возведение в степень рациональных выражений. Тождественные преобразования
Умножение, деление, возведение в степень рациональных выражений. Тождественные преобразования Степень с натуральным показателем. Задания
Степень с натуральным показателем. Задания Первообразная и интеграл
Первообразная и интеграл Коэффициент. Упрощение выражений
Коэффициент. Упрощение выражений Степень числа с натуральным показателем
Степень числа с натуральным показателем Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Задачи по теории относительности
Задачи по теории относительности Древнеяпонские числительные. Задачи
Древнеяпонские числительные. Задачи