Содержание
- 2. Элементы векторной алгебры (матричного анализа). Векторы
- 3. Математика— точная наука в экономике и менеджменте, исследовавшая количественные отношения и экономические формы; более современное понимание:
- 4. Основные понятия Определение. Вектором называется направленный отрезок а с начальной точкой А и конечной точкой В
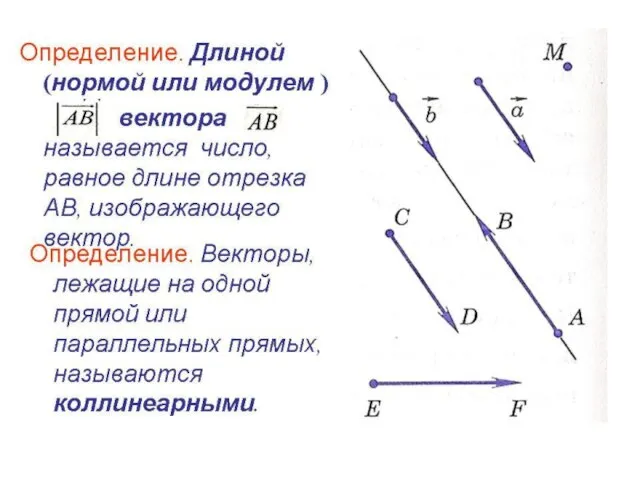
- 5. Определение. Длиной (нормой или модулем ) вектора называется число, равное длине отрезка АВ, изображающего вектор. Определение.
- 6. Определение. Если начало и конец вектора совпадают, например , то такой вектор называют нулевым и обозначают
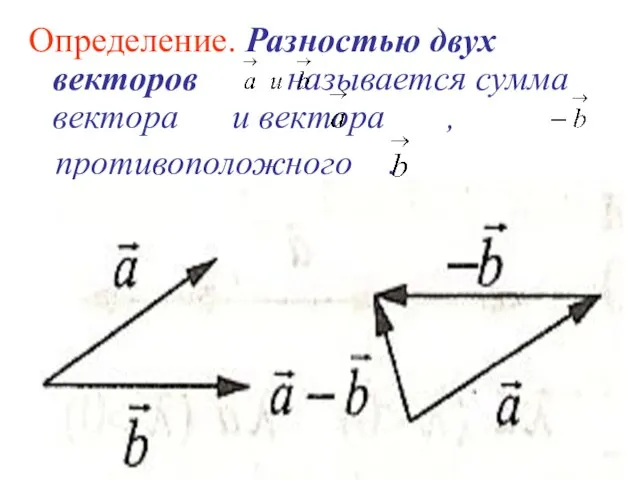
- 7. Определение. Противоположным вектором называется произведение вектора на число (–1), т.е. Определение. Суммой двух векторов и называется
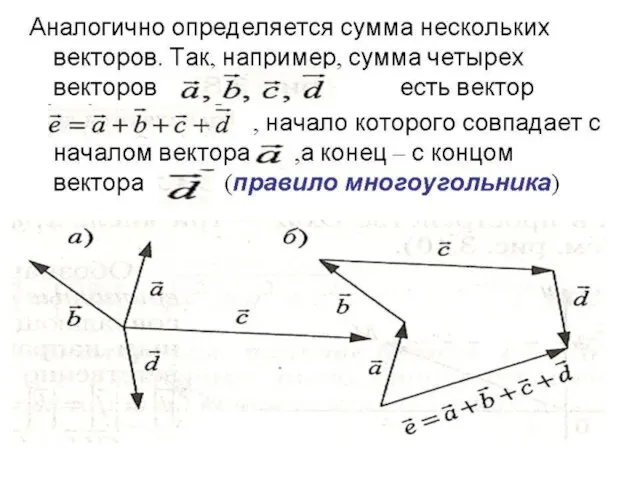
- 8. Аналогично определяется сумма нескольких векторов. Так, например, сумма четырех векторов есть вектор , начало которого совпадает
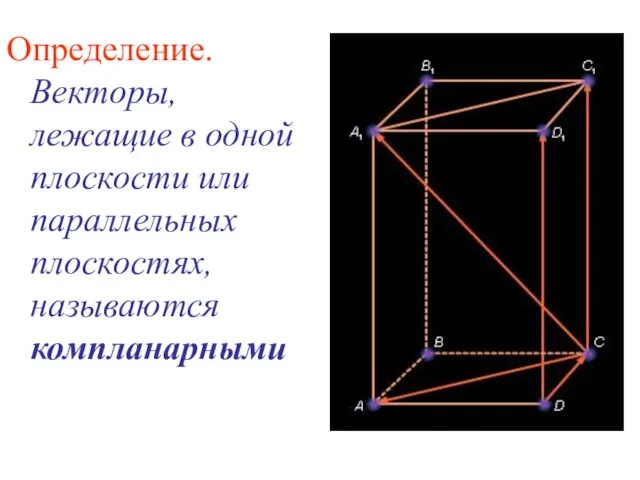
- 9. Определение. Векторы, лежащие в одной плоскости или параллельных плоскостях, называются компланарными
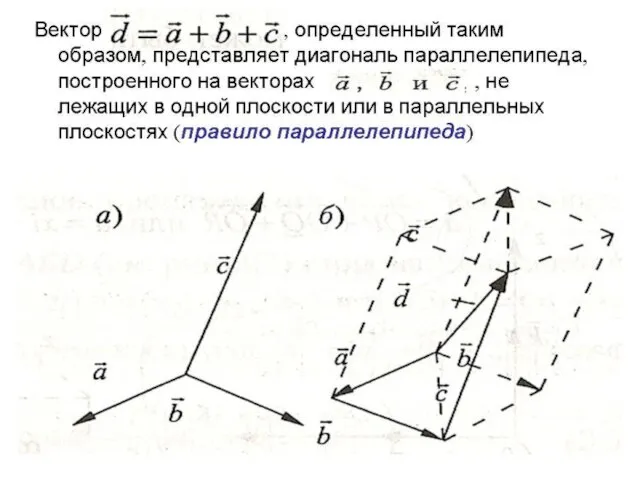
- 10. Вектор , определенный таким образом, представляет диагональ параллелепипеда, построенного на векторах , не лежащих в одной
- 11. Определение. Разностью двух векторов называется сумма вектора и вектора , противоположного .
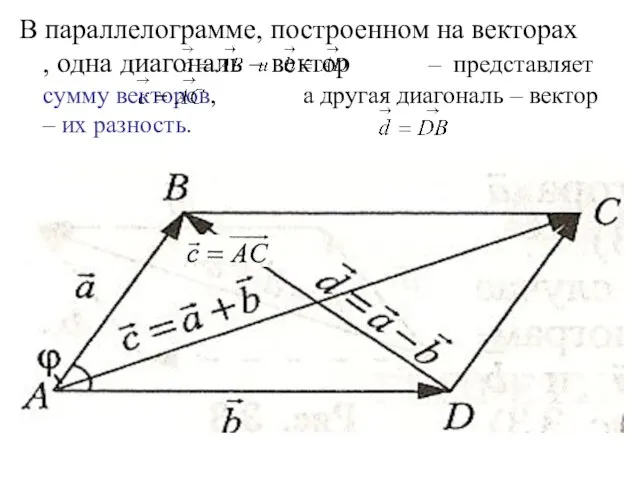
- 12. В параллелограмме, построенном на векторах , одна диагональ – вектор – представляет сумму векторов, а другая
- 13. Если перенести вектор параллельно самому себе и поместить его начало с началом координат, то можно сформулировать
- 14. Обозначим через , единичные векторы , или орты, совпадающие с положительным направлением осей соответственно Ох, Оу,
- 15. Определение. Формула называется разложением вектора по векторам Векторы , сумма которых равна вектору , называются компонентами
- 16. Длина вектора равна корню квадратному из суммы квадратов его координат:
- 17. Определение. Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла
- 18. Если и угол φ = 0, т.е. cosφ = 1, то скалярный квадрат вектора равен квадрату
- 19. Условие перпендикулярности или ортогональности двух векторов и является равенство нулю их скалярного произведения или Условие коллинеарности
- 20. Пример Даны векторы = (3; –7; 2)и = (9;–3; –5) Найти: Вектор ; Длины векторов и
- 21. Найти векторы
- 22. Найти длины векторов
- 23. Найти скалярный квадрат вектора
- 24. Найти скалярное произведение векторов
- 25. Найти угол между векторами
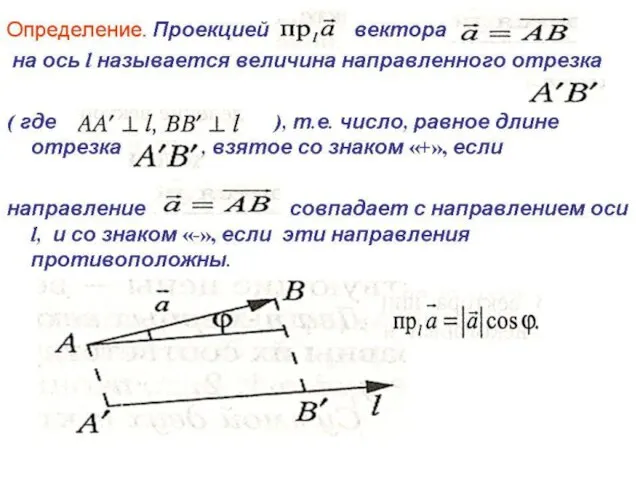
- 26. Определение. Проекцией вектора на ось l называется величина направленного отрезка ( где ), т.е. число, равное
- 27. Определение. Направляющими косинусами вектора называются косинусы углов α, β, γ, образуемых вектором с осями координат. Угол
- 28. Понятие n-мерного пространства Определение. n-мерным вектором называется упорядоченная совокупность n действительных чисел, записанных в виде x=(x1,x2,…,xn),
- 29. Замечание. Компоненты n-мерного вектора обозначают одной буквой, но с разными индексами (в отличие от 2-хмерных или
- 30. Определение. Суммой двух n-мерных векторов называется вектор z = x + y, компоненты которого равны суммам
- 31. Линейные операции над любыми векторами удовлетворяют свойствам: x + y = y + x – коммутативный
- 32. Определение. Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на
- 33. Вопросы для самопроверки: Дайте определение математики как науки. Ее предмет и метод. Как используется математические методы
- 35. Скачать презентацию

























 Случаи вычитания 11 -
Случаи вычитания 11 - Статистические графики
Статистические графики математика гр 32 парність-2.docx
математика гр 32 парність-2.docx Число та цифра 6
Число та цифра 6 Конус. Виды конусов. Конусы в нашей жизни
Конус. Виды конусов. Конусы в нашей жизни Сечения в многогранниках
Сечения в многогранниках Уравнение линии на плоскости. Уравнение фигуры. Уравнение окружности
Уравнение линии на плоскости. Уравнение фигуры. Уравнение окружности Решение задач с помощью уравнений
Решение задач с помощью уравнений Решение задач на движение
Решение задач на движение Понятие спирали
Понятие спирали Геометрические построения
Геометрические построения Элементы теории вероятностей
Элементы теории вероятностей Проценты
Проценты Математические ребусы
Математические ребусы Площади. ОГЭ
Площади. ОГЭ Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Текстовые задачи на движение по прямой
Текстовые задачи на движение по прямой Основное свойство дроби
Основное свойство дроби Две задачи на дроби
Две задачи на дроби Статистические гипотезы
Статистические гипотезы Собираем ягоды. Математика 1 класс. Итоговое повторение. Тренажёр
Собираем ягоды. Математика 1 класс. Итоговое повторение. Тренажёр Конструктивные объекты
Конструктивные объекты Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики?
Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики? Презентация по математике "Что такое понятие" -
Презентация по математике "Что такое понятие" -  Параллельность плоскостей
Параллельность плоскостей Экономический биатлон. “Экономика и математика”. Финал
Экономический биатлон. “Экономика и математика”. Финал Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними
Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними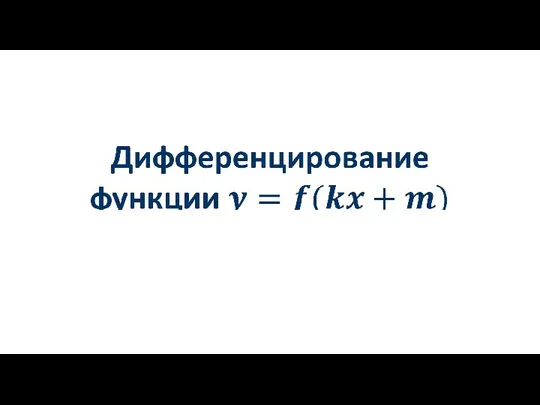 Дифференцирование функции y=f(kx+m)
Дифференцирование функции y=f(kx+m)