Содержание
- 2. Содержание Взаимное расположение прямых в пространстве Параллельные прямые в пространстве Теорема о параллельных прямых Лемма Теорема
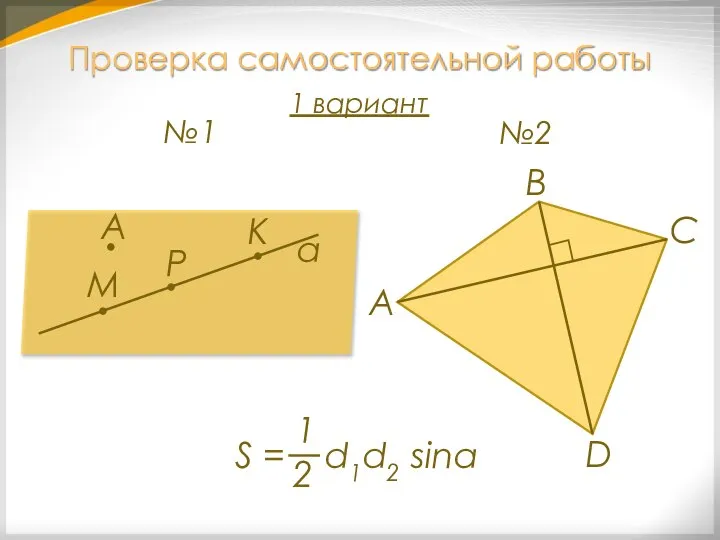
- 3. Проверка самостоятельной работы 1 вариант а M Р К А №1 №2 А С В D
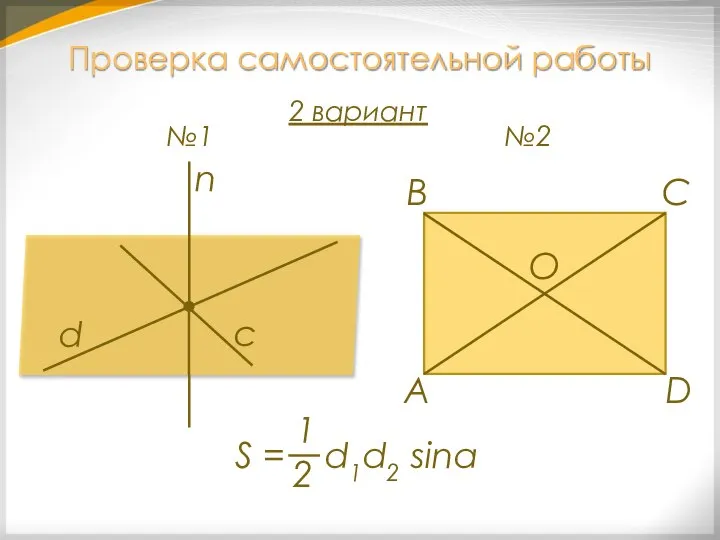
- 4. А С В D 2 вариант с d №1 n O №2 Проверка самостоятельной работы
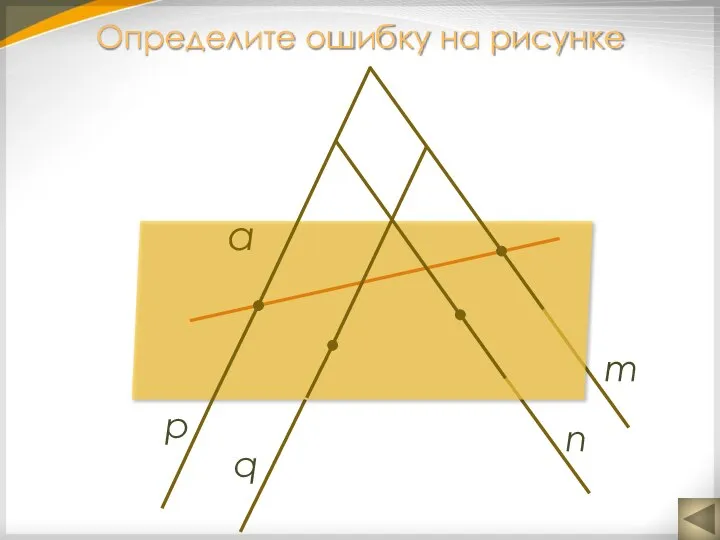
- 5. Определите ошибку на рисунке m n q p α
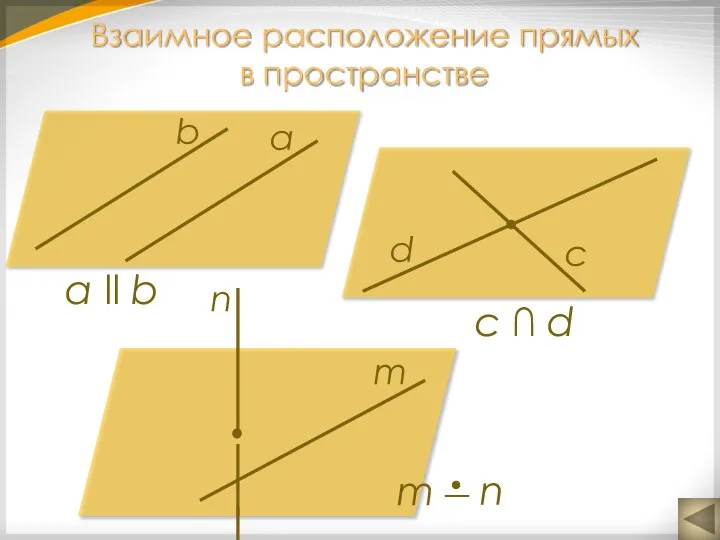
- 6. а ll b c ∩ d Взаимное расположение прямых в пространстве
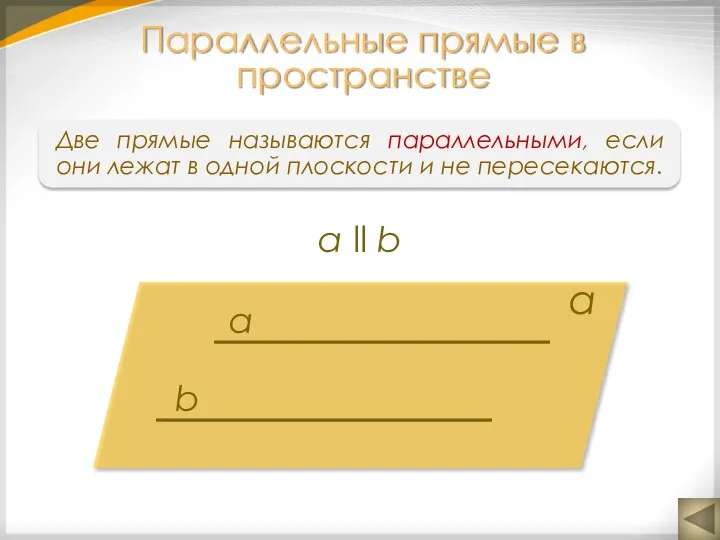
- 7. Параллельные прямые в пространстве а b α а ll b Две прямые называются параллельными, если они
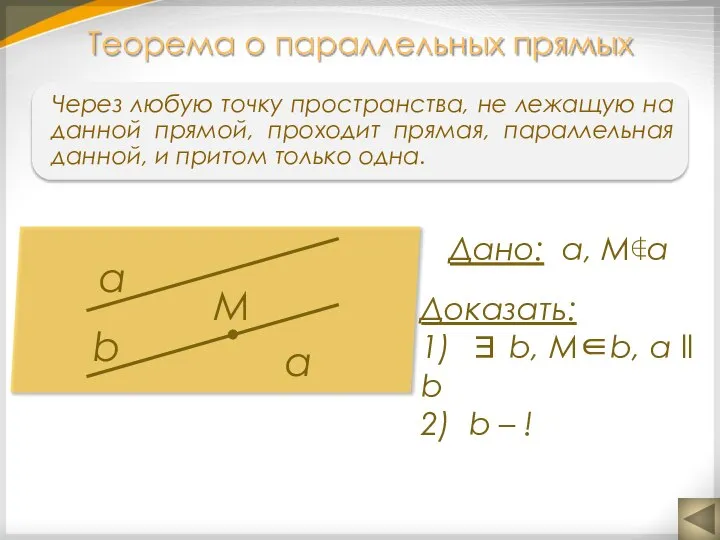
- 8. Теорема о параллельных прямых а b α М Дано: а, М∉а Доказать: 1) ∃ b, М∈b,
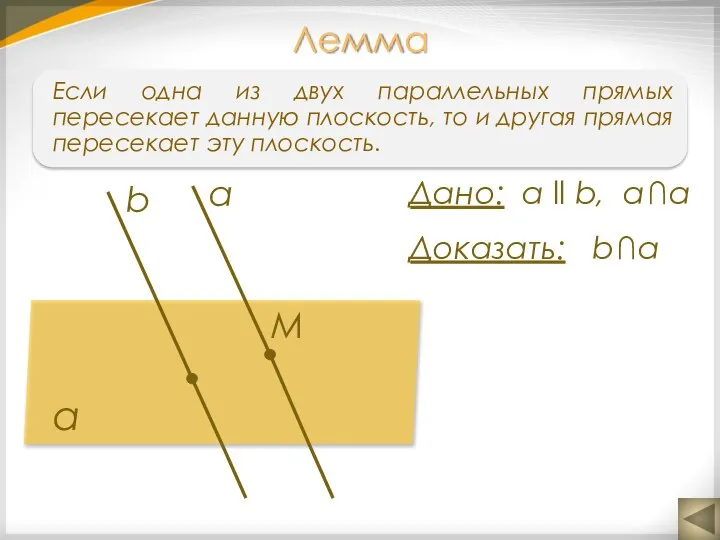
- 9. Лемма a α M b Дано: а ll b, a ∩ α Доказать: b ∩ α
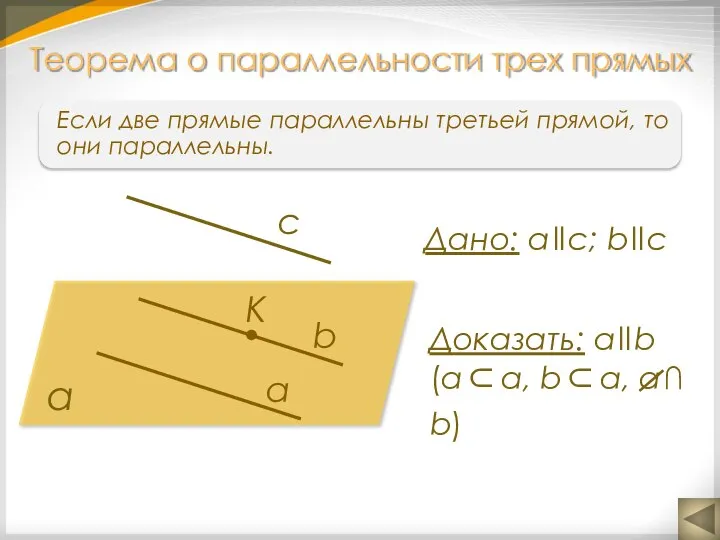
- 10. Если две прямые параллельны третьей прямой, то они параллельны. Теорема о параллельности трех прямых а Дано:
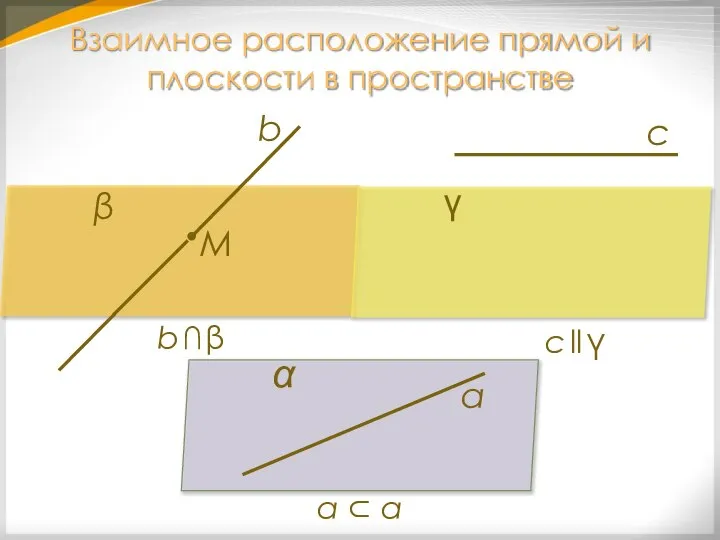
- 11. Взаимное расположение прямой и плоскости в пространстве α а b β М γ с с ll
- 12. Определение параллельных прямой и плоскости α c с ll α Прямая и плоскость называются параллельными, если
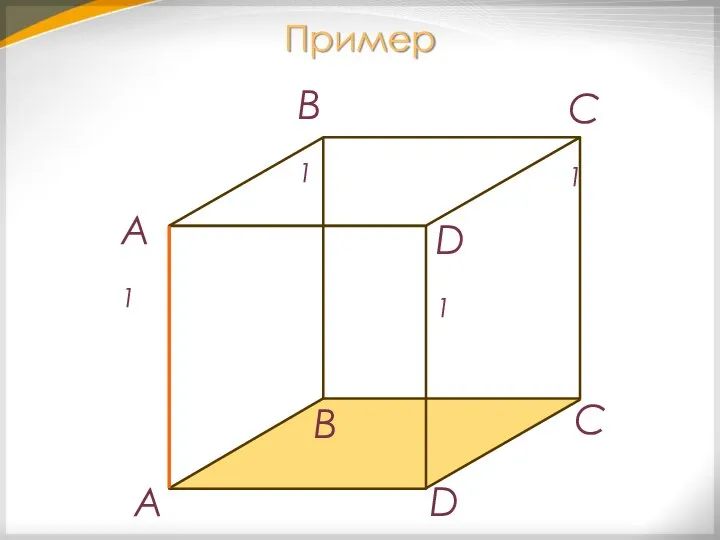
- 13. Пример
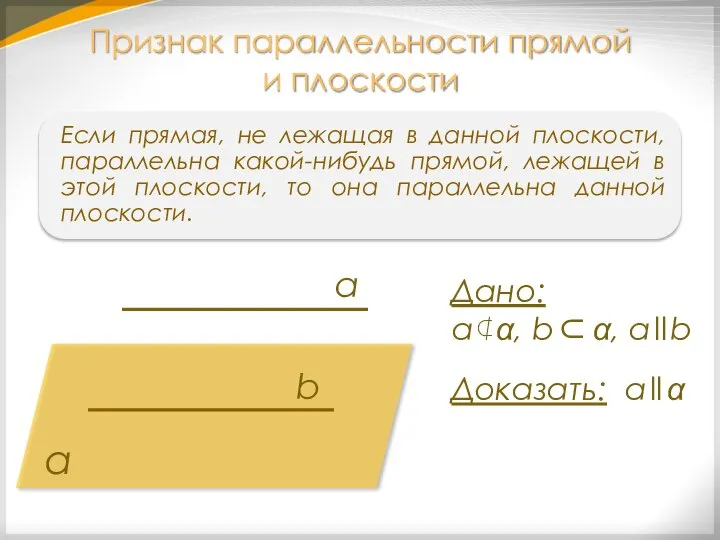
- 14. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она
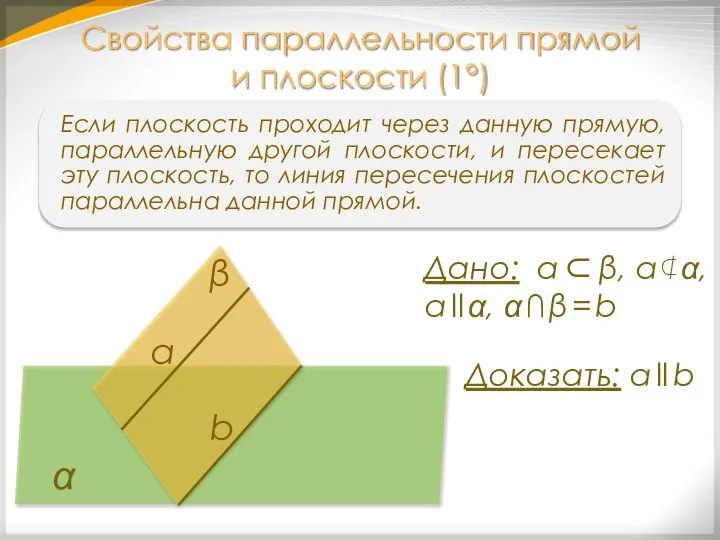
- 15. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения
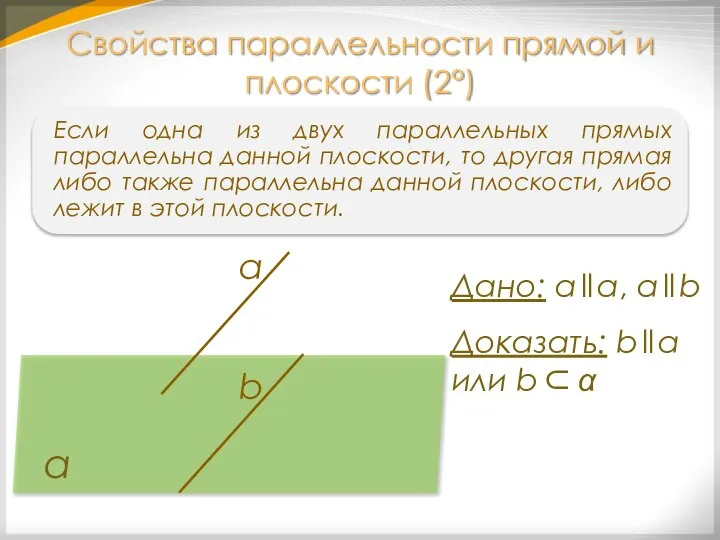
- 16. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной
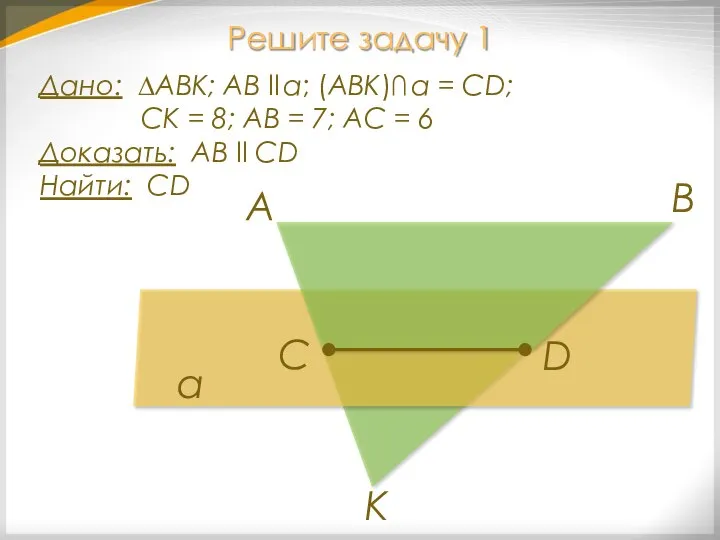
- 17. Решите задачу 1 Дано: ∆АВК; АВ ll α; (АВК)∩ α = СD; СK = 8; АВ
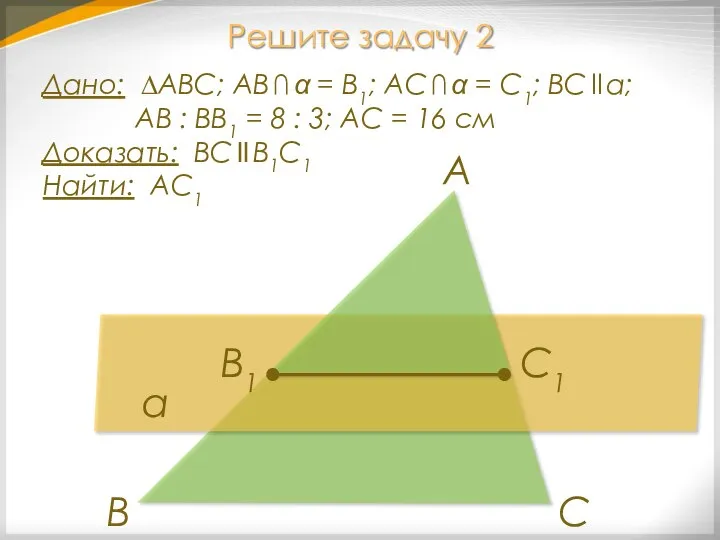
- 18. Решите задачу 2 Дано: ∆АВС; АВ ∩ α = В1; АС ∩ α = С1; ВС
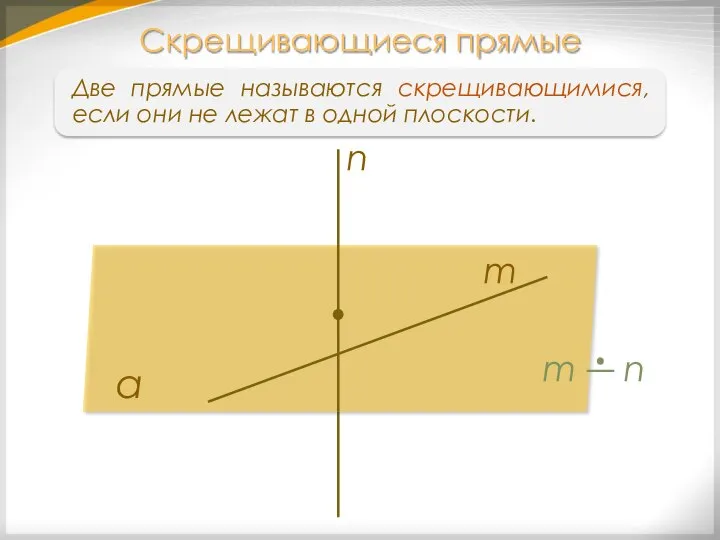
- 19. Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Скрещивающиеся прямые α n m
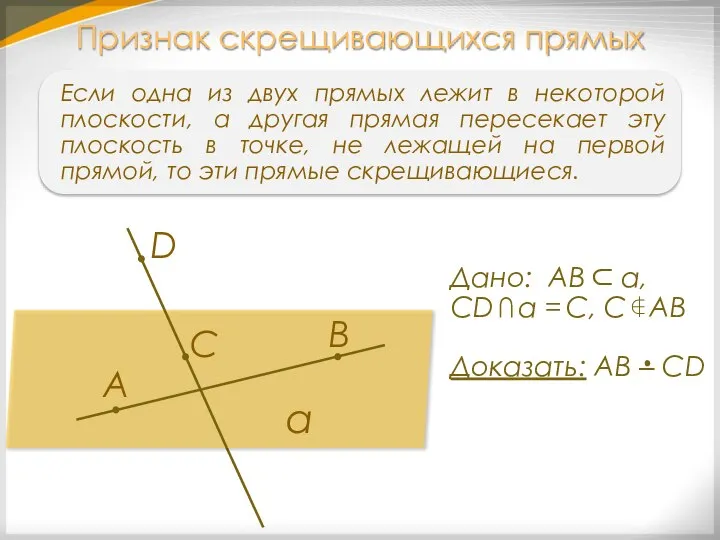
- 20. Признак скрещивающихся прямых Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает
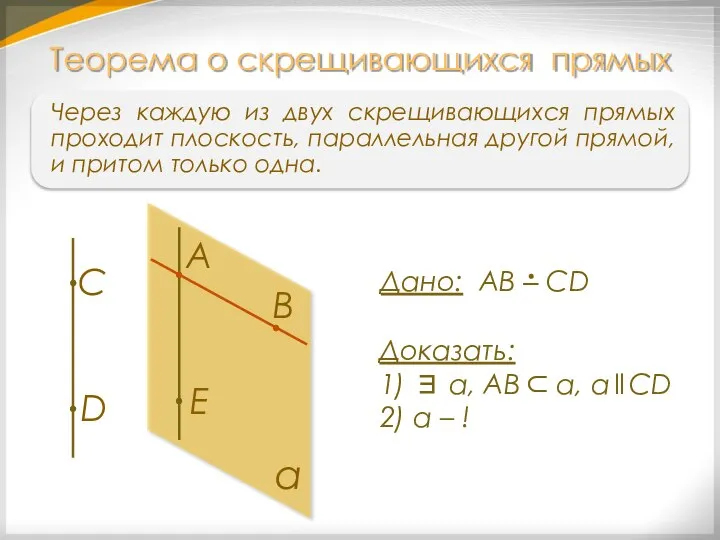
- 21. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. Теорема
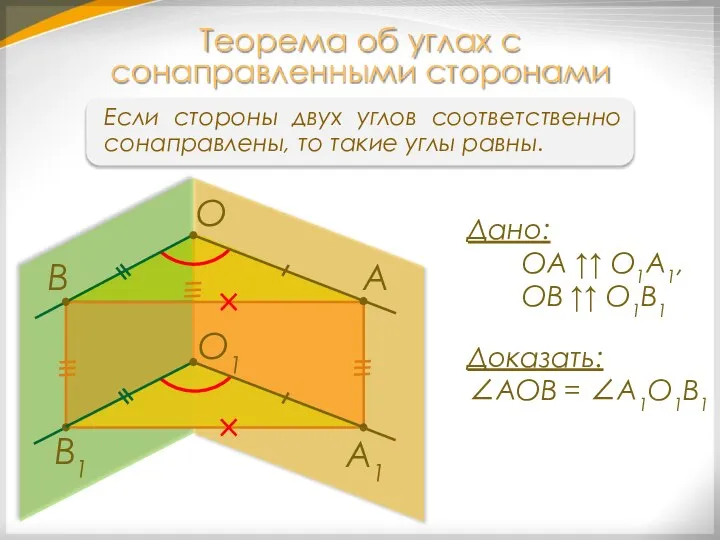
- 22. Если стороны двух углов соответственно сонаправлены, то такие углы равны. Теорема об углах с сонаправленными сторонами
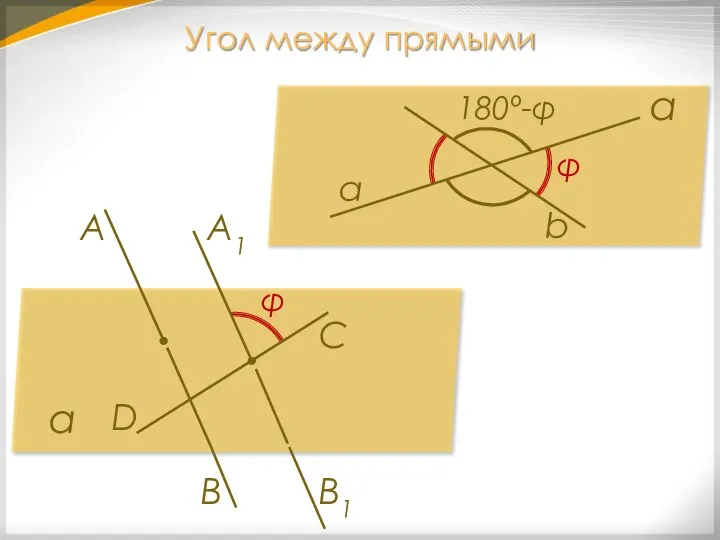
- 23. Угол между прямыми α D А В С φ 180º-φ а b φ А1 В1 α
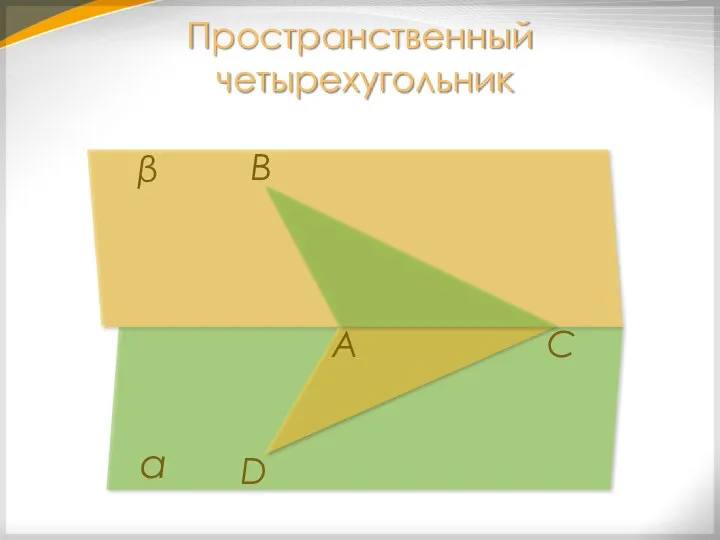
- 24. D С В α β А Пространственный четырехугольник
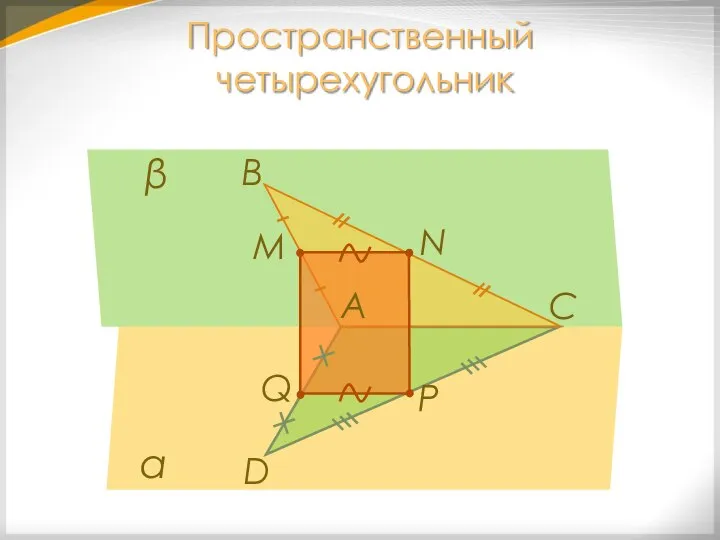
- 25. Пространственный четырехугольник D С В М N P Q α β А
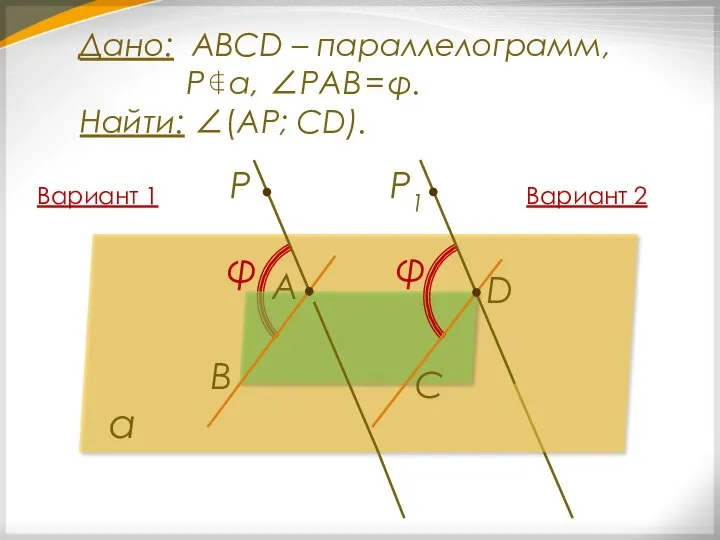
- 26. α В φ P А С D Дано: ABCD – параллелограмм, Р ∉ α, ∠РАВ =
- 28. Скачать презентацию


 Построение графика производной методом касательных
Построение графика производной методом касательных Теория статистики. Предмет, задачи, основные категории и понятия статистики
Теория статистики. Предмет, задачи, основные категории и понятия статистики Таблица сложения в пределах 20
Таблица сложения в пределах 20 Сложение десятичных дробей
Сложение десятичных дробей Ментальная арифметика
Ментальная арифметика Площадь параллелограмма
Площадь параллелограмма Неравенства. Решить систему неравенств
Неравенства. Решить систему неравенств Равнобокая трапеция из бумаги. Работа ножницами
Равнобокая трапеция из бумаги. Работа ножницами Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат
Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат Мишка. Тренажёр - раскраска
Мишка. Тренажёр - раскраска Учимся писать цифры
Учимся писать цифры Соотношения между сторонами и углами в прямоугольном треугольнике
Соотношения между сторонами и углами в прямоугольном треугольнике Презентация на тему Цилиндр
Презентация на тему Цилиндр  Одночлен. Умножение
Одночлен. Умножение Векторно-координатный метод нахождения угла между плоскостями
Векторно-координатный метод нахождения угла между плоскостями Решение задач по теме Параллельность прямой и плоскости
Решение задач по теме Параллельность прямой и плоскости Решение практических задач с помощью арифметической прогрессии
Решение практических задач с помощью арифметической прогрессии Параллельные прямые. Свойства и признаки параллельных прямых
Параллельные прямые. Свойства и признаки параллельных прямых Исследование функций и построение графиков
Исследование функций и построение графиков Планиметрия. Обзор методички
Планиметрия. Обзор методички Prezentatsia_2
Prezentatsia_2 Урок математики с элементами театрализации
Урок математики с элементами театрализации Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства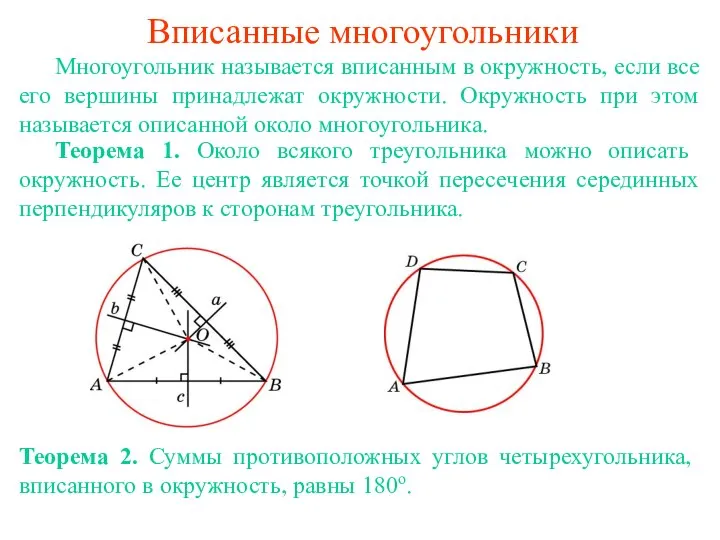 Вписанные и описанные многоугольники
Вписанные и описанные многоугольники множества дистант
множества дистант Домашняя работа. Наурызбай Зарина
Домашняя работа. Наурызбай Зарина Неизвестное делимое
Неизвестное делимое Решение уравнений, содержащих модуль
Решение уравнений, содержащих модуль