Содержание
- 2. 1. Какое уравнение называется дифференциальным уравнением (ДУ)? Уравнение, содержащее производные искомой функции или её дифференциалы. 3.Что
- 3. 5. Определите порядок следующих ДУ: 7. Как называется уравнение вида: Уравнение с разделяющимися переменными Уравнение с
- 4. Уравнение вида , где и – функции, называется линейным дифференциальным уравнением первого порядка. Уравнение называется линейным,
- 5. Какие из данных уравнений являются линейными уравнениями первого порядка, а какие нет и почему? 1) 2)
- 6. Линейное однородное ДУ первого порядка Решите уравнение Решение: (общее решение) (Выразите производную функции через дифференциалы) (Подставьте
- 7. Решите уравнение (общее решение) Линейное однородное ДУ первого порядка Решение:
- 8. Линейное неоднородное ДУ (Метод Иоганна Бернулли) Решите уравнение Алгоритм: 1. Выполните замены в уравнении: 2. Вынесите
- 9. 4. Решите однородное линейное ДУ первого порядка Выразите производную функции через дифференциалы Разделите переменные Проинтегрируйте С=0,
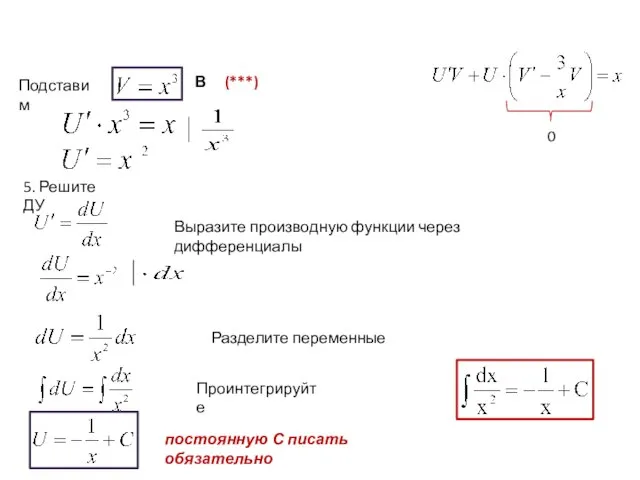
- 10. Подставим В (***) 5. Решите ДУ постоянную С писать обязательно Выразите производную функции через дифференциалы Разделите
- 11. 6. Запишите общий вид решения:
- 13. Скачать презентацию









 Описанная окружность
Описанная окружность Состав числа
Состав числа Логарифм числа. Свойства логарифмов
Логарифм числа. Свойства логарифмов 07_ ОТС_ Основы теории случайных процессов
07_ ОТС_ Основы теории случайных процессов МиРИ Введение. Разд 1. Осн Метр ВЛ
МиРИ Введение. Разд 1. Осн Метр ВЛ Производная функции
Производная функции Готовимся к ОГЭ. Математика
Готовимся к ОГЭ. Математика Преобразование иррациональных выражений
Преобразование иррациональных выражений Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс
Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс Действия с дробями. Многогранники
Действия с дробями. Многогранники Уравнения и способы их решения
Уравнения и способы их решения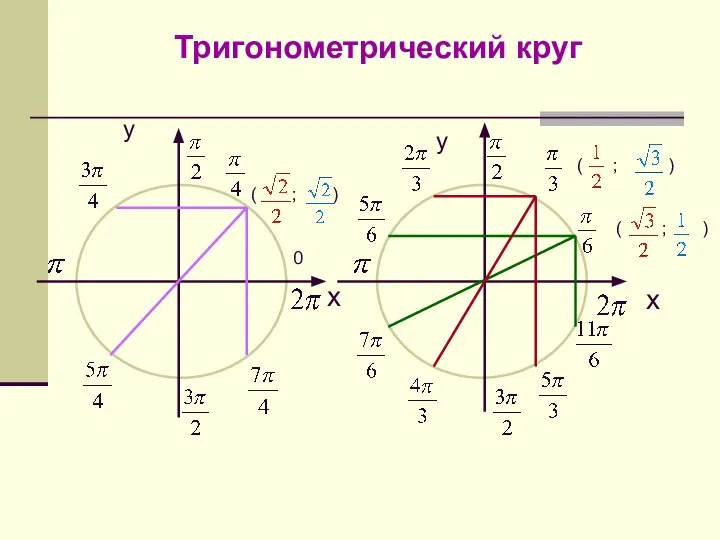 Тригонометрический круг
Тригонометрический круг Параллельные прямые в архитектуре
Параллельные прямые в архитектуре Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Решение задач по теме треугольники
Решение задач по теме треугольники Уравнение сферы
Уравнение сферы Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3
Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3 Четырехугольники
Четырехугольники Игра - тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра - тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Сложение целых чисел
Сложение целых чисел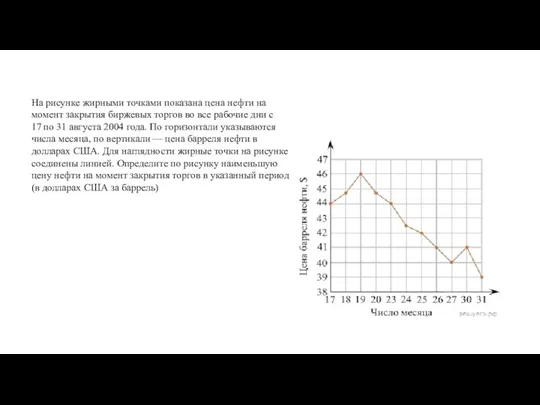 Вариант 1
Вариант 1 Элементы статистической обработки данных
Элементы статистической обработки данных Презентация на тему Касательная к окружности
Презентация на тему Касательная к окружности  Презентация на тему Координаты (4 класс)
Презентация на тему Координаты (4 класс)  Прямоугольный треугольник . Решение задач
Прямоугольный треугольник . Решение задач Формулы двойного аргумента
Формулы двойного аргумента Подобие треугольников и решение практических задач задач
Подобие треугольников и решение практических задач задач Интересные факты в математике
Интересные факты в математике