Презентация на тему Принцип Дирихле

Петер Густав Лежен Діріхле
1805 - 1859
Німецький математик.
Народився в Дюрені.
у 1822-1827 р. був домашним вчителем у Парижі. Входив у кружок молодих вчених, які групувалися навколо
Ж. Фур'є.
1831-1855рр.-професор Берлінського університету
Зробив ряд великих відкритій у теорії чисел.

“ Традиційне ” формулювання
Якщо у 5 клітках розміститься 6 кроликів, то принаймні в одній з них міститься не менше двох кролів.

Класичне формулювання
Якщо (n + 1) кроликів сидять в n ящиках, то знайдеться ящик, у якому сидить, принаймні, два кролики

День народження
У школі 400 учнів. Доведіть, що хоча б двоє з них народилися в один день року.

Пряма і трикутник
Доведіть, що ніяка пряма не може перетинати всі три сторони трикутника.

Рішення:
Пряма ділить площину на дві півплощини, які ми назвемо "клітками".
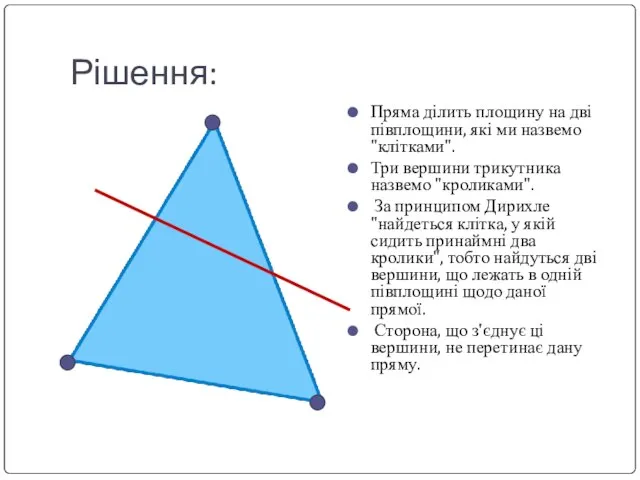
Три вершини трикутника назвемо "кроликами".
За принципом Дирихле "найдеться клітка, у якій сидить принаймні два кролики", тобто найдуться дві вершини, що лежать в одній півплощині щодо даної прямої.
Сторона, що з'єднує ці вершини, не перетинає дану пряму.

Забута планета
На кожній із планет якоїсь сонячної системи перебуває астроном, що спостерігає найближчу планету. Відстані між планетами попарно різні.
Доведіть, що якщо число планет непарне, то яку-небудь планету ніхто не спостерігає.

Доведення.

На планеті Зям-лям
На далекій планеті Зям-лям, що має форму кулі, суша займає більше половини поверхні планети.
Доведіть, що можна прорити прямий тунель, що проходить через центр планети і з'єднує сушу із сушею.

Доведення.
Припустимо, що кожній крапці світового океану відповідає протилежна крапка суши, тоді світовий океан і суша центральносиметричні, а площі їх рівні, що суперечить умові задачі.
Отже, можна прорити прямий тунель, що проходить через центр планети і з'єднує сушу із сушею.

Зайці в клітці
У клітці живуть зайці: 7 чорних і 5 сірих.
Скільки голодному вовку в темряві треба витягти із клітки зайців, щоб серед них було не менше 2-х чорних і не менше 3-х сірих?

Так як можливий самий несприятливий для вовка варіант: спочатку він витягне 7 чорних, і лише потім 3 сірих зайців, то в темряві йому треба витягти із клітки 7 + 3 = 10 зайців.
Відповідь. 10 зайців.

Допоможіть Буратіно
Кіт Базиліо пообіцяв Буратіно відкрити велику таємницю, якщо він складе чарівний квадрат
6 х 6 із чисел +1, -1, 0 так, щоб всі суми по рядках, по стовпцях і по більших діагоналях були різні.

Це неможливо !
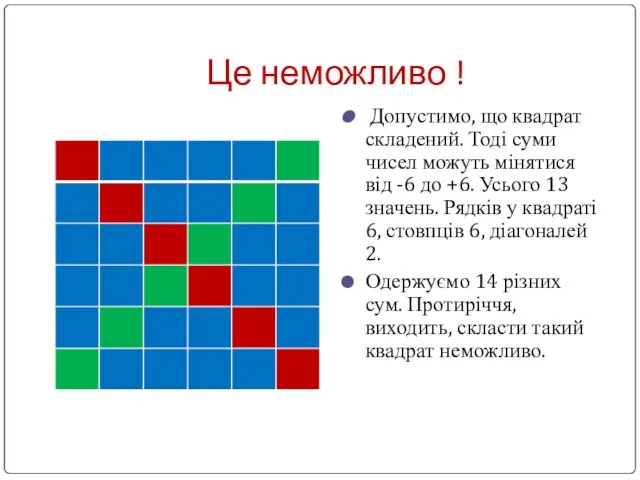
Допустимо, що квадрат складений. Тоді суми чисел можуть мінятися від -6 до +6. Усього 13 значень. Рядків у квадраті 6, стовпців 6, діагоналей 2.
Одержуємо 14 різних сум. Протиріччя, виходить, скласти такий квадрат неможливо.

Розв'яжи сам
Шість школярів з'їли сім цукерок.
а) Доведіть, що один з них з'їв не менш двох цукерок.
б) чи вірно, що хтось з'їв рівно дві цукерки?

Розв'яжи сам
Грані куба пофарбовані в 2 кольори.
Доведіть, що найдуться дві сусідні однокольорові грані.

Рішення:
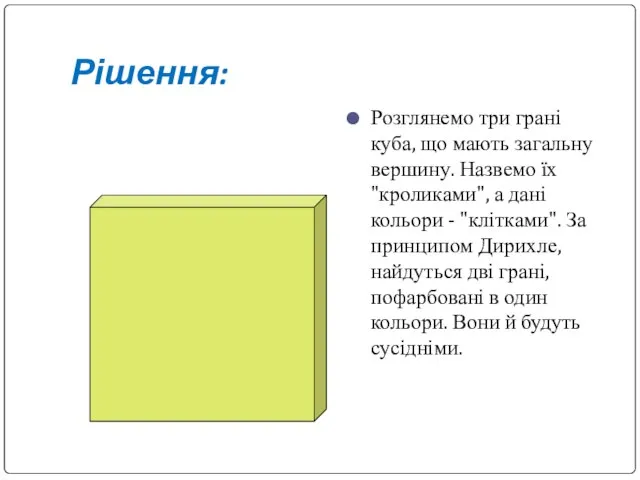
Розглянемо три грані куба, що мають загальну вершину. Назвемо їх "кроликами", а дані кольори - "клітками". За принципом Дирихле, найдуться дві грані, пофарбовані в один кольори. Вони й будуть сусідніми.