Содержание
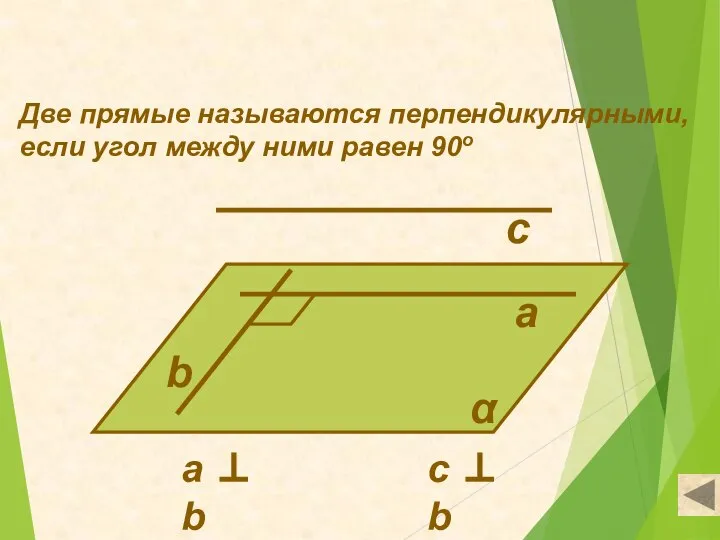
- 2. Две прямые называются перпендикулярными, если угол между ними равен 90о а b с а ⊥ b
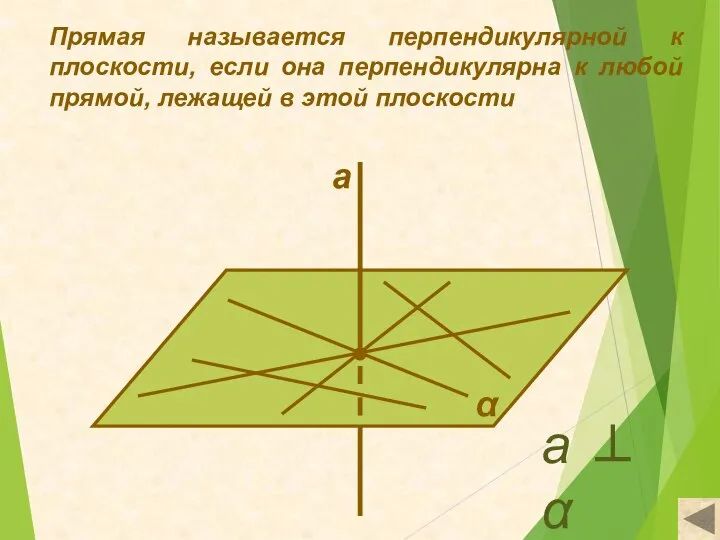
- 3. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости α
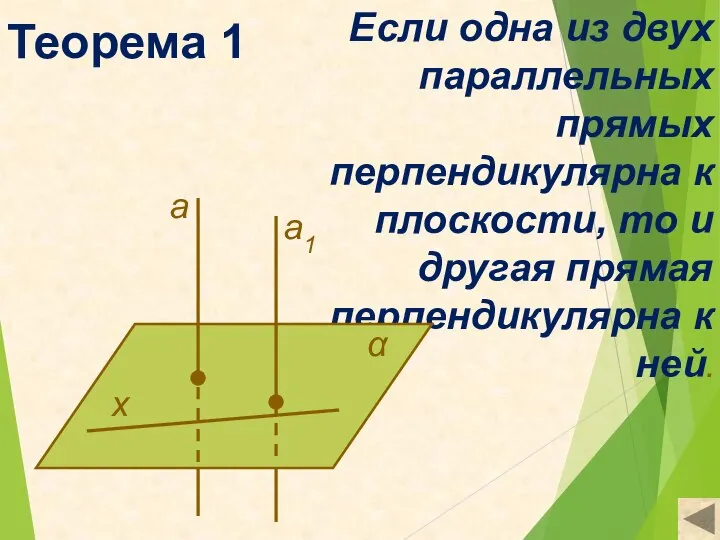
- 4. Теорема 1 Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна
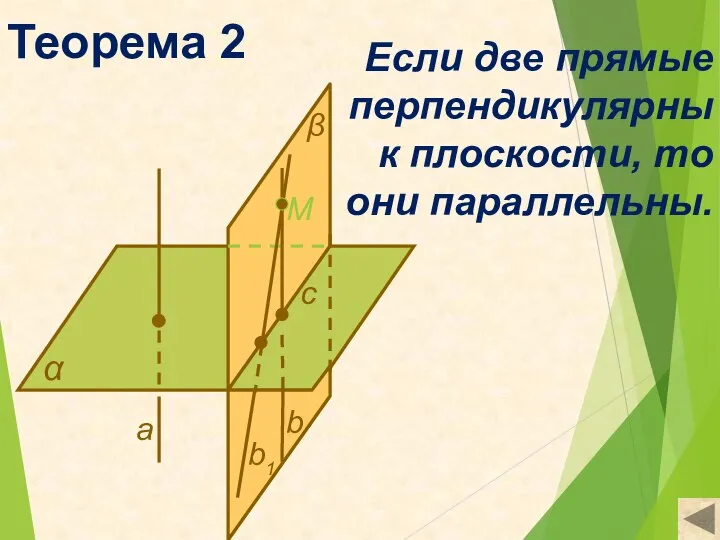
- 5. Теорема 2 α Если две прямые перпендикулярны к плоскости, то они параллельны. M с
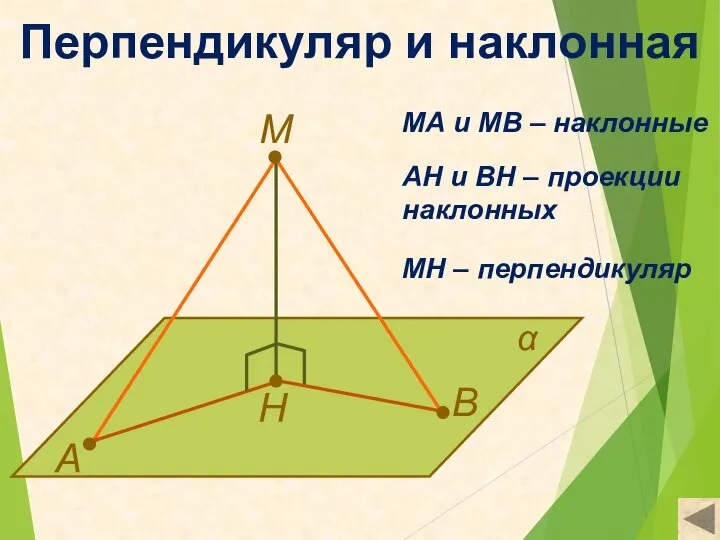
- 6. Перпендикуляр и наклонная М А В Н α МА и МВ – наклонные АН и ВН
- 7. Перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к
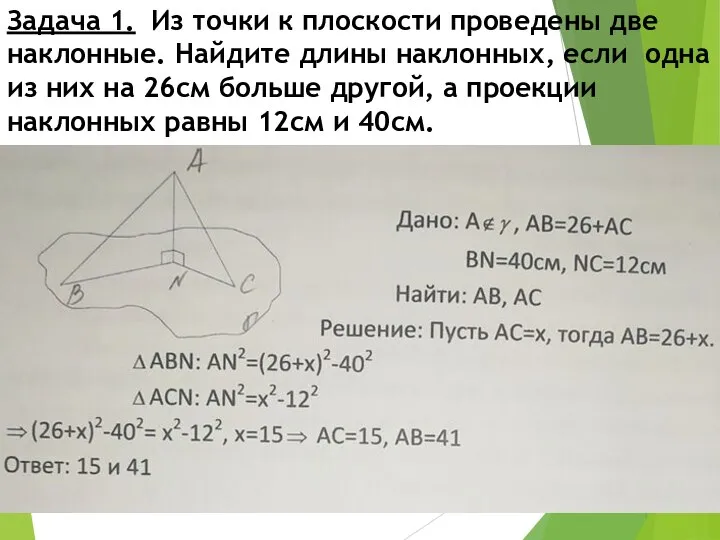
- 8. Задача 1. Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если одна из них
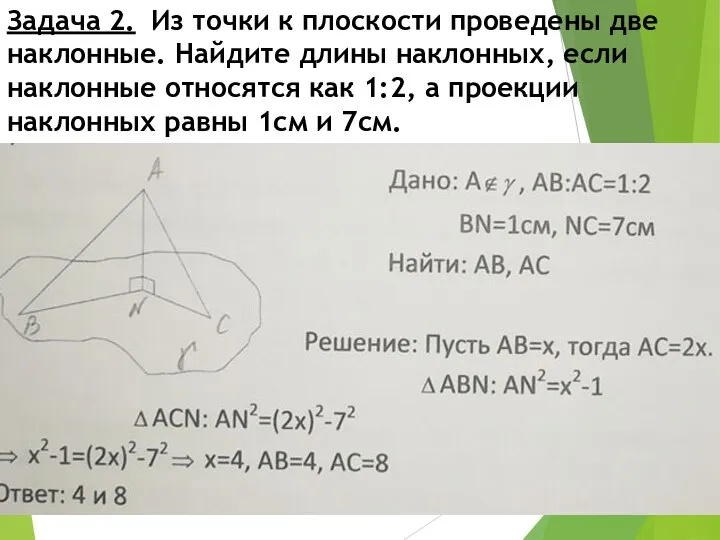
- 9. Задача 2. Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если наклонные относятся как
- 10. Задача 3. Найдите расстояние от середины отрезка АВ до плоскости, не пересекающей этот отрезок, если расстояние
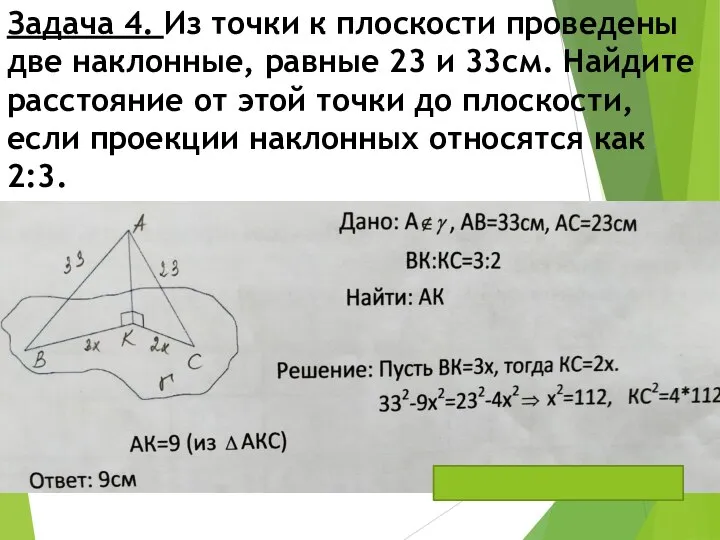
- 11. Задача 4. Из точки к плоскости проведены две наклонные, равные 23 и 33см. Найдите расстояние от
- 12. Задача 5. Из точки, не принадлежащей данной плоскости, проведены к ней две наклонные, сумма длин которых
- 13. Задача 6. Найдите расстояние от середины отрезка АВ до плоскости, не пересекающей этот отрезок, если расстояния
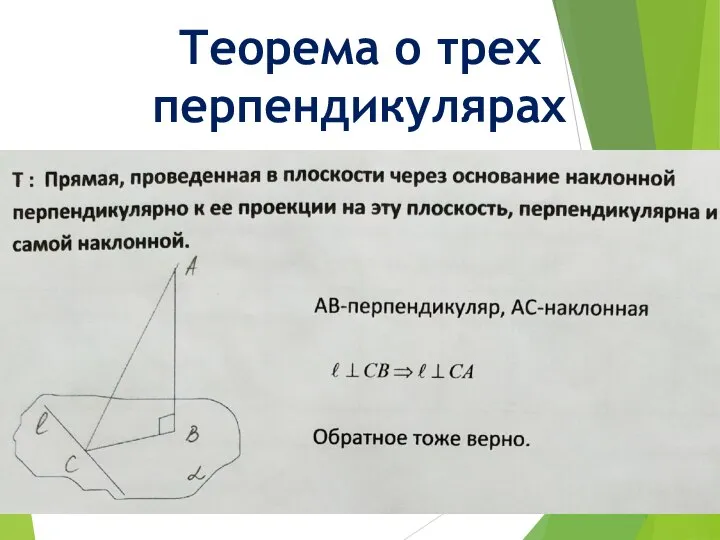
- 14. Теорема о трех перпендикулярах
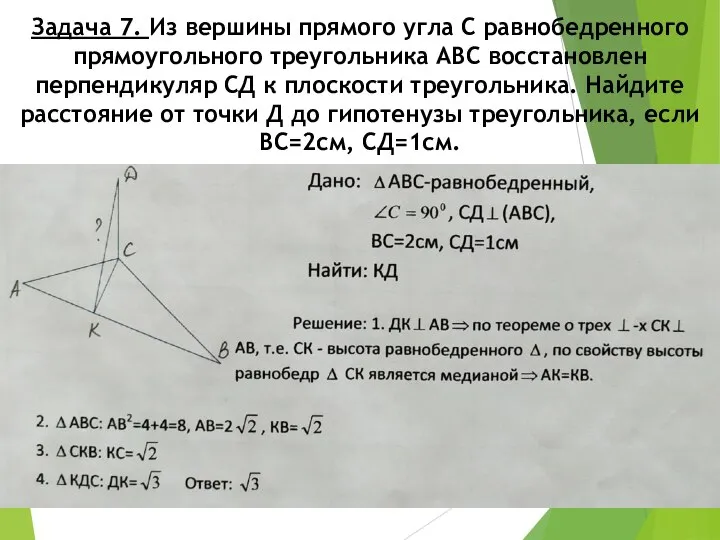
- 15. Задача 7. Из вершины прямого угла С равнобедренного прямоугольного треугольника АВС восстановлен перпендикуляр СД к плоскости
- 16. Задача 8: В равнобедренном треугольнике АВС основание СВ =12м, боковая сторона 10м. Из вершины А проведен
- 18. Скачать презентацию





 Алгоритмы направленного перебора
Алгоритмы направленного перебора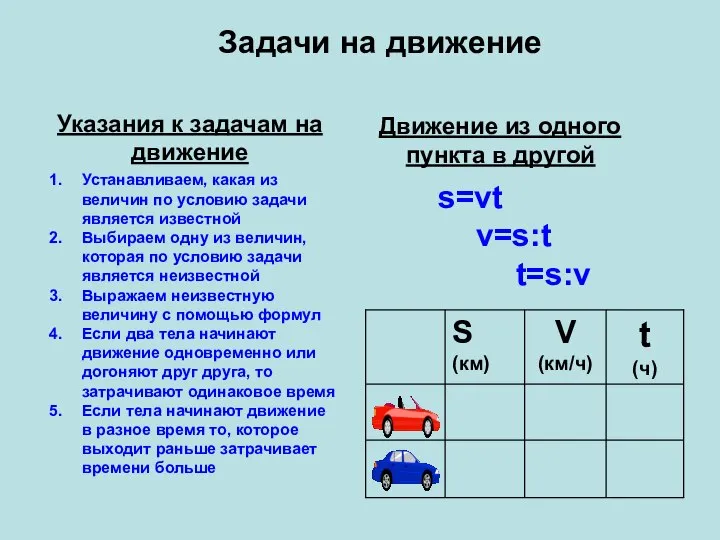 Задачи на движение Указания к задачам на движение
Задачи на движение Указания к задачам на движение Графики функций
Графики функций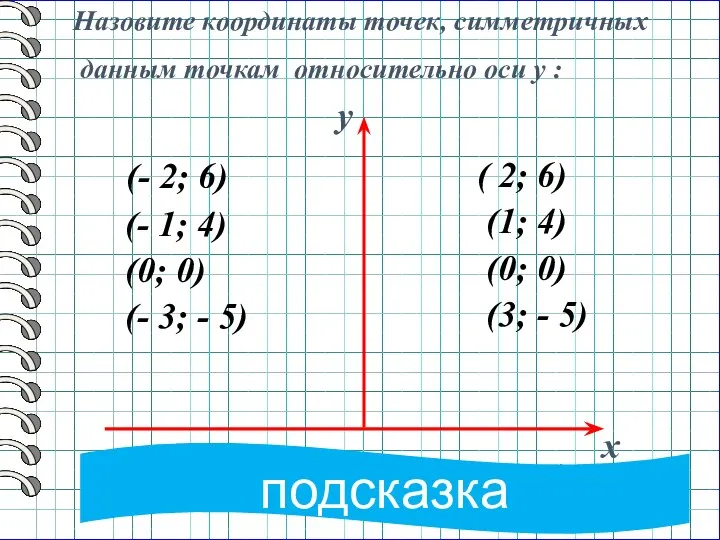 Квадратичная функция
Квадратичная функция Арифметическая прогрессия
Арифметическая прогрессия Космос
Космос Поворот и центральная симметрия
Поворот и центральная симметрия Теорема Виета
Теорема Виета Иллюстрации географических объектов на Луне
Иллюстрации географических объектов на Луне Математика в карточных фокусах
Математика в карточных фокусах Примеры
Примеры Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля
Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля  Понятие вектора
Понятие вектора Бином Ньютона. Треугольник Паскаля
Бином Ньютона. Треугольник Паскаля Решение задач на прямую и обратную пропорциональность
Решение задач на прямую и обратную пропорциональность Распознавание и называние геометрических фигур
Распознавание и называние геометрических фигур Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Функция. График функции
Функция. График функции Сайы. Умумий малюмат
Сайы. Умумий малюмат Презентация на тему Обыкновенные дроби (6 класс)
Презентация на тему Обыкновенные дроби (6 класс)  Контрольная работа № 9
Контрольная работа № 9 Геометрия на каждом уроке
Геометрия на каждом уроке Наименьшее и наибольшее значение функции. Задачи
Наименьшее и наибольшее значение функции. Задачи Способы решения задач на смеси и сплавы
Способы решения задач на смеси и сплавы Площадь фигур. Решение задач
Площадь фигур. Решение задач Подготовка к ВПР
Подготовка к ВПР Решение квадратных уравнений. Повторительно-обобщающий урок
Решение квадратных уравнений. Повторительно-обобщающий урок Математика для детей (игры)
Математика для детей (игры)