Понятие функции

Понятие функции
Соответствие между двумя
множествами

Определение
Функция (от латин. слова functio — совершение, исполнение);
Функцией называется соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого множества.

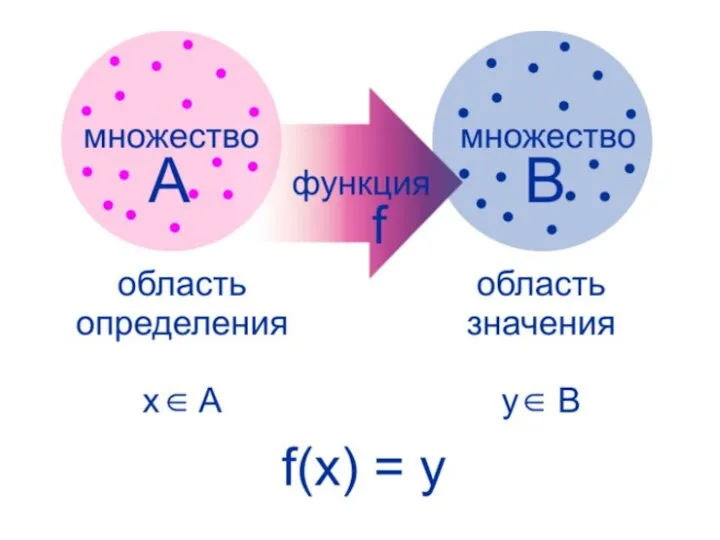
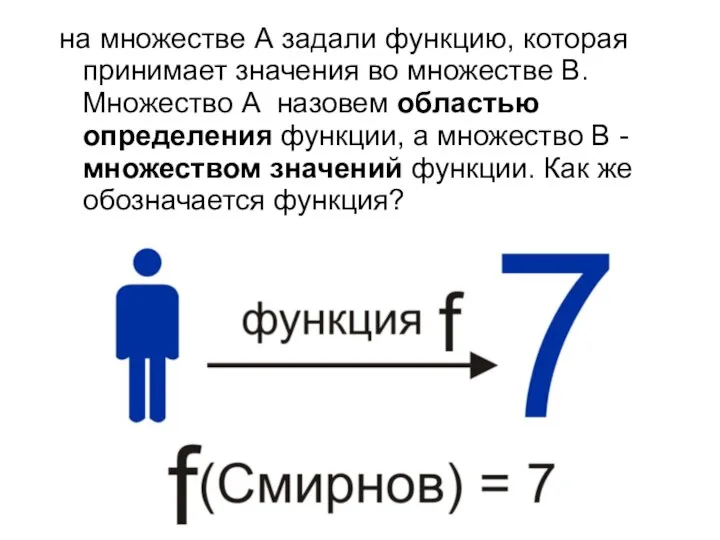
на множестве А задали функцию, которая принимает значения во множестве B. Множество А назовем областью определения функции, а множество В - множеством значений функции. Как же обозначается функция?

Не любая зависимость — функция!

Таблица квадратов задается функцией?
х — переменная, множеством значений которой является множество двузначных чисел (Х)
у — переменная, множеством значений которой являются их квадраты.
у=х2

Определение
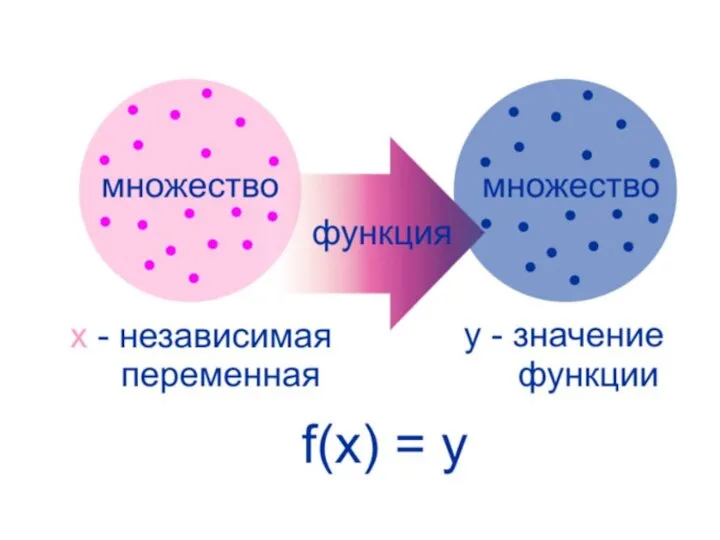
Элемент х из множества Х можно выбрать любой, а вот элемент у из множества У выберется при этом сам, по правилу f.
Поэтому говорят, что
х - это независимая переменная (или аргумент функции f),
у — зависимая переменная или функция, значение функции f.

Терминология
Область определения функции — множество значений аргумента
Область значений функции — все значения, которые принимает функция
Если переменная у является функцией от переменной х, то используется запись:
у = f(х)
f - имя функции, правило соответствия

Способы задания функции
1. описанием - каждому двузначному числу поставим в соответствие его квадрат.
2. аналитически, т. е. с помощью формулы:
3. таблицей: