Содержание
- 2. ОСНОВНЫЕ ТАВТОЛОГИИ 1. |=A→(B→A) 2. |=(A→B)→((A→(B→C))→(A→C)) 3. |=A→(B→A&B) 4А. |=A&B→A 4Б. |=A&B→B 5А. |=A→A∨B 5Б. |=B→A∨B
- 3. ПРАВИЛО ВЫВОДА (MODUS PONENS): (MP). ОПР. ВЫВОДОМ НАЗЫВАЕТСЯ КОНЕЧНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ФОРМУЛ, КАЖДАЯ ИЗ КОТОРЫХ ЯВЛЯЕТСЯ АКСИОМОЙ
- 4. ОПР. ФОРМУЛА A НАЗЫВАЕТСЯ ВЫВОДИМОЙ В ИСЧИСЛЕНИИ ВЫСКАЗЫВАНИЙ ИЛИ ТЕОРЕМОЙ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ (ОБОЗНАЧЕНИЕ |=A), ЕСЛИ СУЩЕСТВУЕТ
- 5. ОПР. ФОРМУЛА A НАЗЫВАЕТСЯ ВЫВОДИМОЙ ИЗ МНОЖЕСТВА ФОРМУЛ Γ (ОБОЗНАЧЕНИЕ Γ |= A), ЕСЛИ СУЩЕСТВУЕТ ВЫВОД
- 6. ПРАВИЛА ВВЕДЕНИЯ И УДАЛЕНИЯ
- 7. ЕСЛИ Γ ∪ {A} ├ B, ТО Γ ├ (A → B). ДОКАЗАТЕЛЬСТВО. ИНДУКЦИЯ ПО ДЛИНЕ
- 8. 9)A→A 10)(А → В) → ((В → С)(А → С)) 11)( А → (¬ А →
- 9. 20) ¬ (А ∧ В) ~ (¬ А ∨ ¬ В) 21) ¬ (А → В)
- 10. 1. A→(A→A) СХ. 1; 2. (A→(A→A))→((A→((A→ A)→ A))→(A→A), ГДЕ B=A→A, C=A, СХ. АКС. 2; 3. (A→((A→A)→A))→(A→A)
- 11. ЕСЛИ ДОКАЖЕМ ЧТО СУЩЕСТВУЮТ : А → В, В → С, А ├ С А →
- 12. ТРЕБУЕТСЯ ДОКАЗАТЬ А ├ (¬ А → В) 1) А, ¬ А ├ В (СЛАБОЕ УДАЛЕНИЕ
- 13. ├ А & (В & С) ~ (А & В) & С 1) ├ А &
- 14. 1) А, А → В, ¬ В ├ В (УДАЛЕНИЕ → , МР ) 2) А,
- 15. 1 ЧАСТЬ : ┣ A&(B&C) → (A&B)&C 2 ЧАСТЬ : ┣ (A&B)&C → A&(B&C) ДОКАЗАТЕЛЬСТВО 1
- 16. А) ├ А ∨ (В ∨ С) → (А ∨ В) ∨ С Б) ├ (А
- 17. ├ ((А & В) → (В & А) & ├ (В & А) → (А &
- 18. ├ (А ∨ В → В ∨ А) & (В ∨ А → А ∨ В)
- 19. A) A & (В ∨ С) ├ (А & В) ∨ (А & С) Б) (А
- 20. ДОКАЖЕМ ЧАСТЬ Б ПО СЛЕДУЮЩЕЙ СХЕМЕ: (А & В) ∨ (А & С) ├ A (*)
- 21. А) ├ A ∨ (В & С) → (А ∨ В) & (А ∨ С) Б)
- 22. ДОКАЖЕМ ЧАСТЬ Б: ├ (А ∨ В) & (А ∨ С) → A ∨ (В &
- 23. А) ├ ¬ (А ∨ В) → (¬ А & ¬ В) Б) ├ (¬ А
- 24. А) ├ ¬ (А & В) → (¬ А ∨ ¬ В) Б) ├ (¬ А
- 25. I. |=¬¬A ~ A II. |=A ~ ¬¬ A ЧАСТЬ I 1. ¬¬A|=A (УДАЛЕНИЕ ¬) 2.
- 26. 1. ¬A, ¬ (A∨¬A) |=¬A∨A (ВВЕДЕНИЕ ∨) 2. ¬A, ¬ (A∨¬A) |=¬(A∨¬A) (СВОЙСТВО ВЫВОДИМОСТИ ) 3.
- 27. 1.|= ¬ (A&¬A)~ ¬A∨¬A 2. |= A∨¬A (ПО ФОРМУЛЕ №23) 3. |=¬ (A&¬A) 24) |= ¬
- 29. Скачать презентацию




















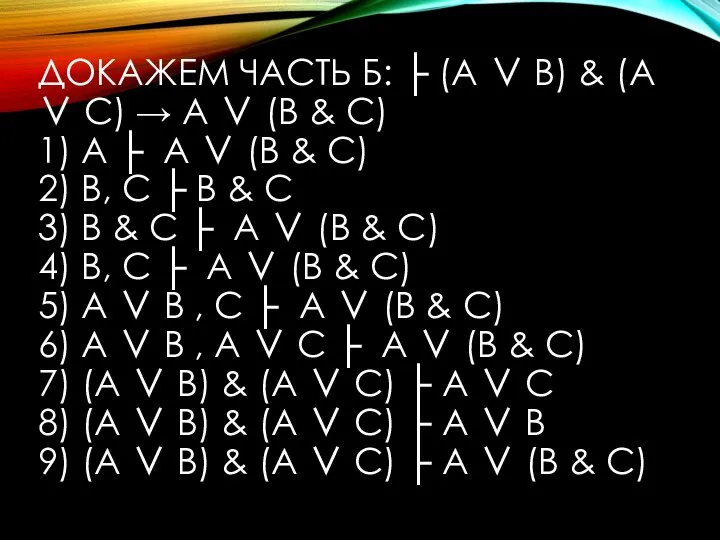




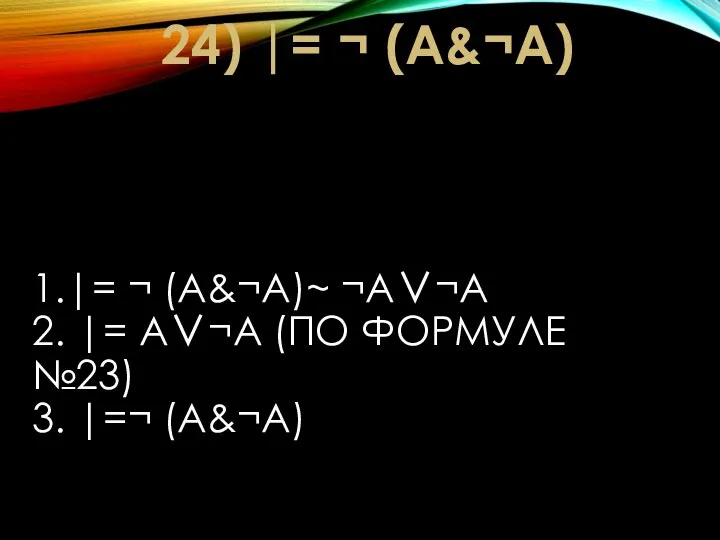
 #УчимсяСМарусей. Фрагмент урока математики в 5 классе с использованием умной колонки
#УчимсяСМарусей. Фрагмент урока математики в 5 классе с использованием умной колонки Метод неопределенных коэффициентов. Теорема о рациональном корне многочлена с целыми коэффициентами
Метод неопределенных коэффициентов. Теорема о рациональном корне многочлена с целыми коэффициентами Сложение чисел. Как можно найти значение суммы 7 + 7
Сложение чисел. Как можно найти значение суммы 7 + 7 Численные методы механики сплошных сред. Индивидуальные задания
Численные методы механики сплошных сред. Индивидуальные задания Методы доказательства теорем: прямой метод и метод от противного
Методы доказательства теорем: прямой метод и метод от противного Backpropagation
Backpropagation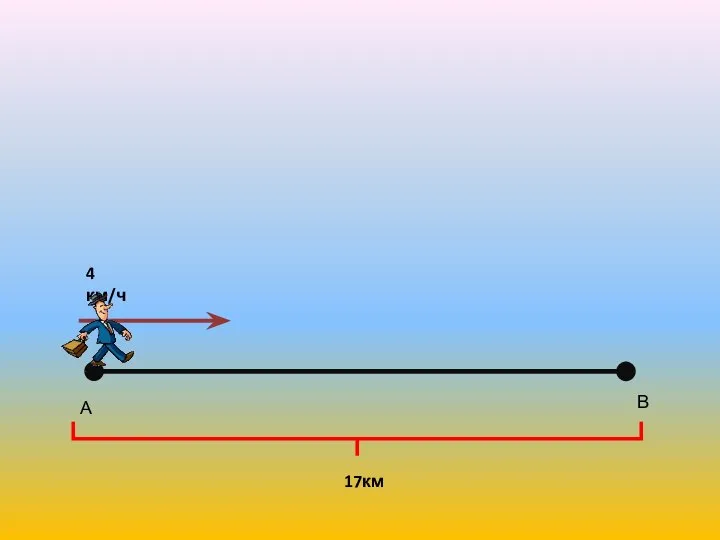 Решение задач на движение
Решение задач на движение Треугольники. ЕГЭ
Треугольники. ЕГЭ Гастроли госпожи математики. Внеклассное мероприятие для учащихся 10 классов
Гастроли госпожи математики. Внеклассное мероприятие для учащихся 10 классов Координатная плоскость (урок 2)
Координатная плоскость (урок 2) Умножение натуральных чисел 5 класс
Умножение натуральных чисел 5 класс Производная сложной функции
Производная сложной функции Фигуры в пространстве
Фигуры в пространстве Правила деления. (6 класс)
Правила деления. (6 класс) Презентация на тему КООРДИНАТНАЯ ПЛОСКОСТЬ (6 КЛАСС)
Презентация на тему КООРДИНАТНАЯ ПЛОСКОСТЬ (6 КЛАСС)  Площадь криволинейной трапеции
Площадь криволинейной трапеции Площадь прямоугольника
Площадь прямоугольника Прибавить и вычесть число 1
Прибавить и вычесть число 1 Првильные многоугольники
Првильные многоугольники Длиннее, короче (1 класс)
Длиннее, короче (1 класс) Теория вероятностей
Теория вероятностей matematika_6_kl_04_10
matematika_6_kl_04_10 Круг, окружность, длина и площадь окружности
Круг, окружность, длина и площадь окружности Учимся писать цифры
Учимся писать цифры Задачи на уменьшение числа на несколько единиц
Задачи на уменьшение числа на несколько единиц Больше, меньше, столько же
Больше, меньше, столько же Презентация по математике "Выполните задание !" -
Презентация по математике "Выполните задание !" -  Методика изучения Массы
Методика изучения Массы