Содержание
- 2. Математическая статистика — наука о математических методах систематизации и использования статистических данных для решения научных и
- 3. Предположим, что необходимо изучить множество объектов по какому-либо признаку. Большая совокупность объектов для исследования, называется генеральной
- 4. Рассеяние значений изучаемого признака генеральной совокупности от их генеральной средней оценивают генеральной дисперсией, или генеральным средним
- 5. Рассеяние значений изучаемого признака генеральной совокупности от их генеральной средней оценивают генеральной дисперсией, или генеральным средним
- 6. Часто возникает ситуация, при которой изучить всю генеральную совокупность практически невозможно. Тогда изучают не всю генеральную
- 7. Множество объектов, отобранные из генеральной совокупности, называются выборкой, или выборочной совокупностью. Свойство объектов выборки должно соответствовать
- 9. Для дискретной случайной величины X, принимающей конечное число значений, законом распределения в теории вероятностей считается таблица.
- 12. Находятся они по тем же формулам, что и их аналоги, но, как мы уже упоминали, вероятность
- 13. Указанные характеристики дают хорошее приближение для математического ожидания и дисперсии изучаемой случайной величины. Однако дисперсия имеет
- 16. Пусть мы имеем следующий набор данных. Отметим, что величина x представляет измерения диаметра древесного ствола у
- 17. Данные измерений очевидно содержат ошибки. Сюда входят как ошибки измеряющих, так и вытекающие из ограниченной точности
- 20. Завершая усреднение, выберем представителем каждого интервала его середину и будем считать, что она встретилась столько раз,
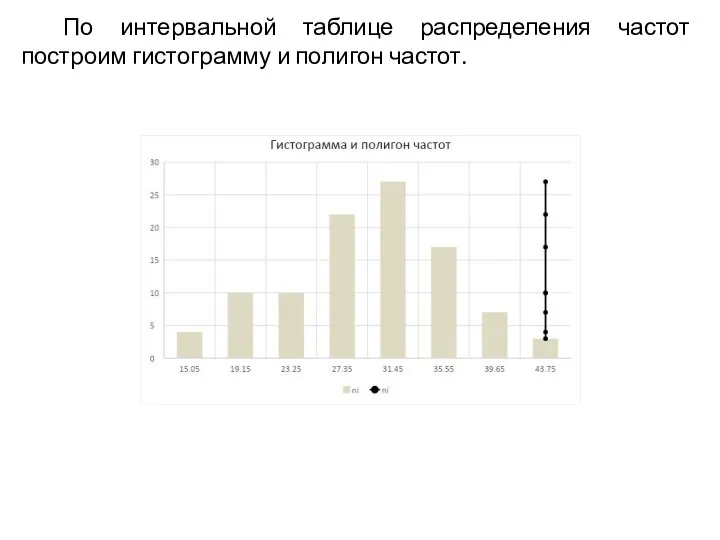
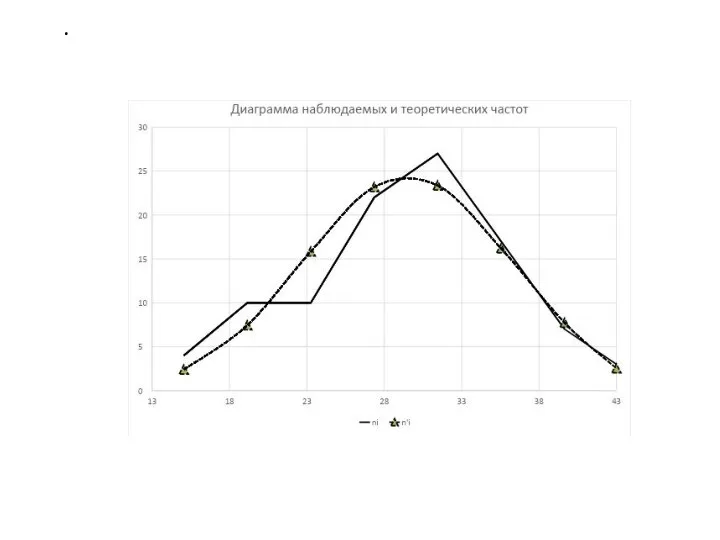
- 21. По интервальной таблице распределения частот построим гистограмму и полигон частот.
- 22. Вычисление основных характеристик выборки. Чтобы завершить предварительную обработку данных, по формулам, указанным выше, найдем точечные оценки
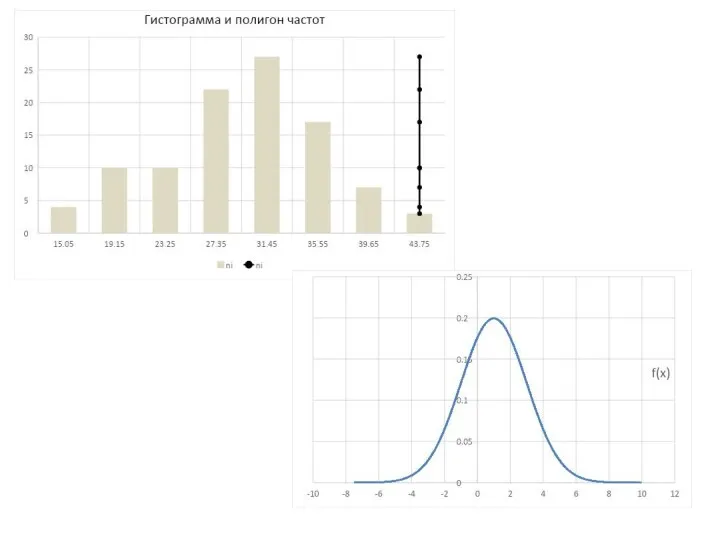
- 24. По интервальной таблице распределения частот мы построили гистограмму и полигон частот. Если получившаяся конструкция похожа на
- 25. .
- 28. После подсчетов получаем таблицу.
- 29. .
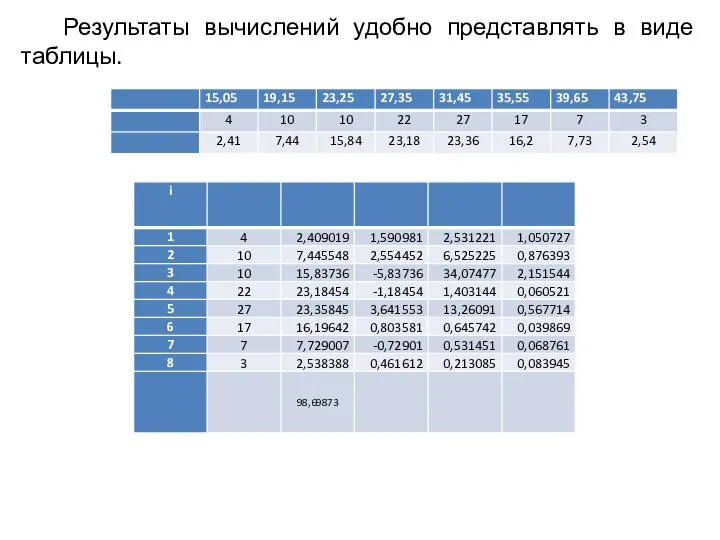
- 31. Результаты вычислений удобно представлять в виде таблицы.
- 34. Отыскание интервальных оценок параметров нормального распределения. Найдём интервальные оценки математического ожидания и среднего квадратического отклонения генеральной
- 36. Сделаем окончательный вывод. Проведенные исследования показали, что генеральная совокупность случайной величины x, выражающей диаметры ствола деревьев
- 37. .
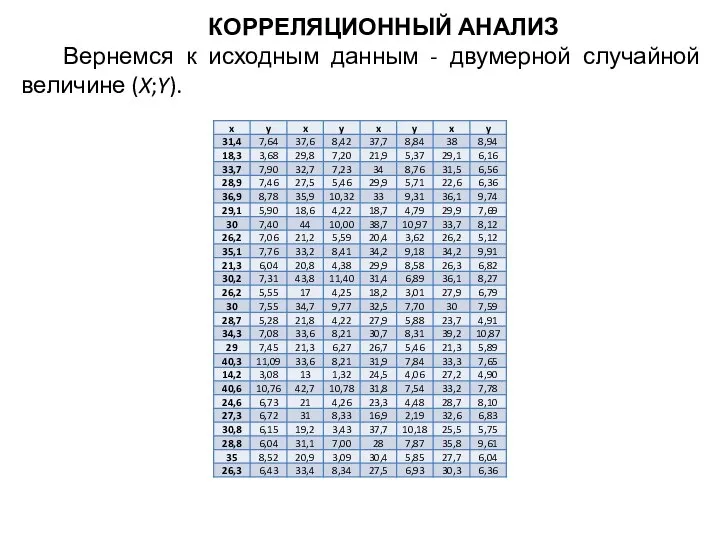
- 38. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ Вернемся к исходным данным - двумерной случайной величине (X;Y).
- 39. Для каждой из двух случайных величин X и Y отдельно мы построили интервальные и вариационные ряды,
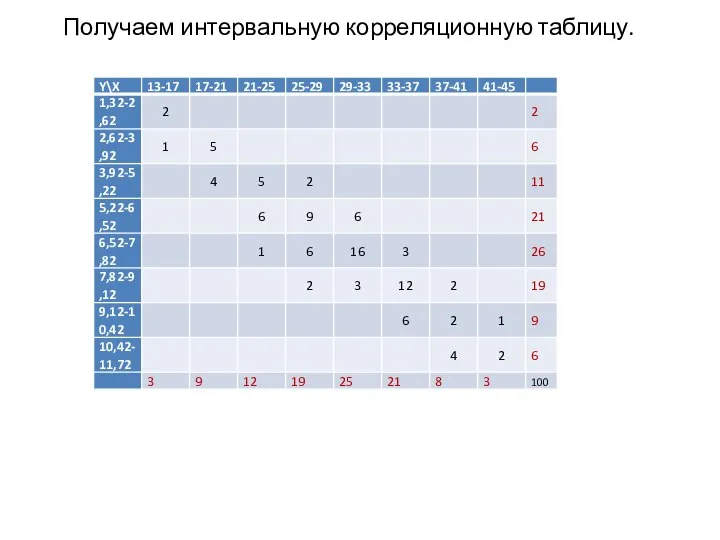
- 40. Построим интервальную корреляционную таблицу. По горизонтали отложим интервалы X, а по вертикали по Y. В ячейки
- 41. Получаем интервальную корреляционную таблицу.
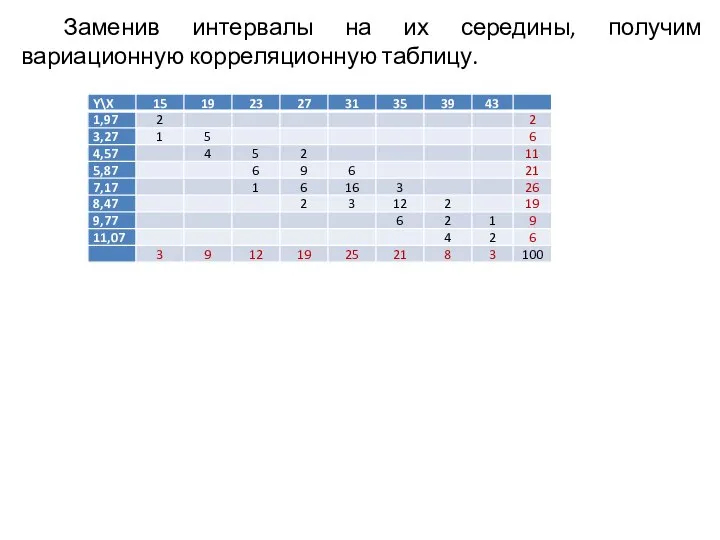
- 42. Заменив интервалы на их середины, получим вариационную корреляционную таблицу.
- 44. В нашем примере
- 47. Уравнение линейной регрессии X на Y имеет вид
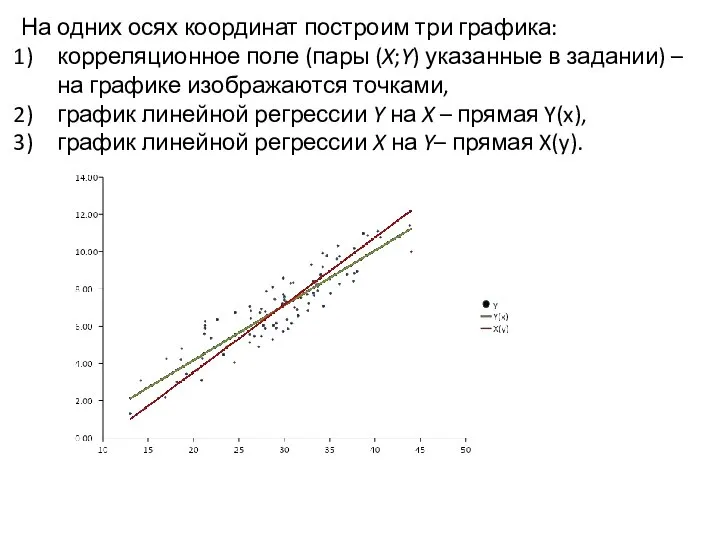
- 48. На одних осях координат построим три графика: корреляционное поле (пары (X;Y) указанные в задании) – на
- 50. .
- 52. Скачать презентацию







































 Пирамида. Её элементы. Правильная пирамида. Усечённая пирамида
Пирамида. Её элементы. Правильная пирамида. Усечённая пирамида Презентация на тему Умножение числа 2
Презентация на тему Умножение числа 2  Умножение на двузначное число
Умножение на двузначное число Решение задач на проценты, растворы и сплавы
Решение задач на проценты, растворы и сплавы Дискретная математика. Повторение арифметических действий
Дискретная математика. Повторение арифметических действий Математика. Лекция 1
Математика. Лекция 1 Векторная алгебра
Векторная алгебра Пирамида. Решение задач
Пирамида. Решение задач Таблицы сложения и вычитания с числом 2
Таблицы сложения и вычитания с числом 2 Rinjka liinija
Rinjka liinija Сравнение чисел
Сравнение чисел Численное дифференцирование
Численное дифференцирование Презентация на тему Игра Что? Где? Когда? 10 класс по математике
Презентация на тему Игра Что? Где? Когда? 10 класс по математике 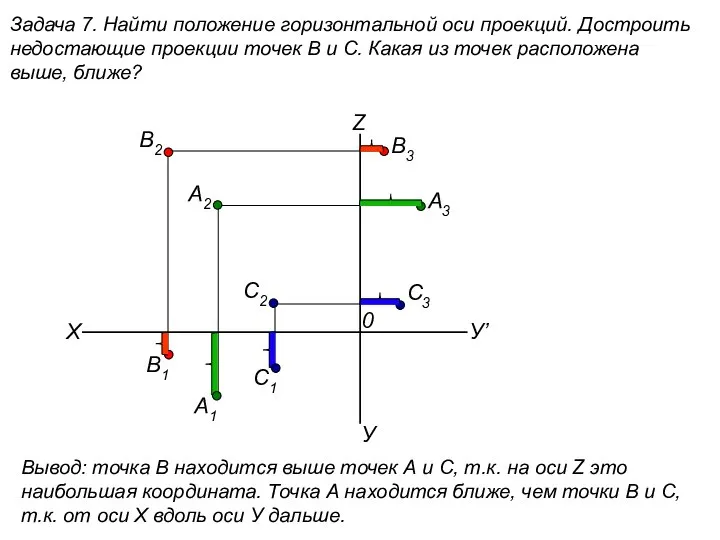 Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7)
Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7) Степень числа
Степень числа Подобие треугольников. Решение задач по готовым чертежам. 8 класс
Подобие треугольников. Решение задач по готовым чертежам. 8 класс Решение задач в Excel
Решение задач в Excel Контрольная работа. Умножение и деление
Контрольная работа. Умножение и деление Письменное умножение трёхзначного числа на однозначное
Письменное умножение трёхзначного числа на однозначное Четырехугольники. Параллелограмм
Четырехугольники. Параллелограмм Применение производной к исследованию функции и построению графика функции
Применение производной к исследованию функции и построению графика функции Регулятивные удд
Регулятивные удд Пирамида. Виды пирамид
Пирамида. Виды пирамид Строение функции, свойства, графики
Строение функции, свойства, графики Угол между прямой и плоскостью
Угол между прямой и плоскостью Рассчитать площадь и периметр прямоугольника по двум известным сторонам. Алгоритм решения подобных задач
Рассчитать площадь и периметр прямоугольника по двум известным сторонам. Алгоритм решения подобных задач Таблица умножения на 3
Таблица умножения на 3 Структура учебного модуля № 5 Многогранники. ( 20 часов)
Структура учебного модуля № 5 Многогранники. ( 20 часов)