Содержание
- 2. Площади и объем цилиндра. Решение задач.
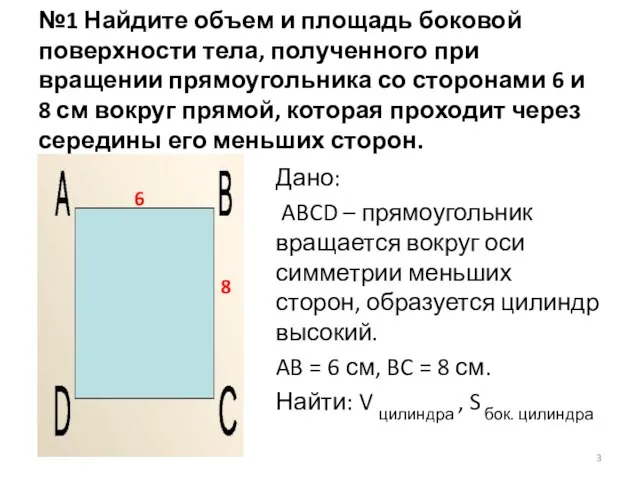
- 3. №1 Найдите объем и площадь боковой поверхности тела, полученного при вращении прямоугольника со сторонами 6 и
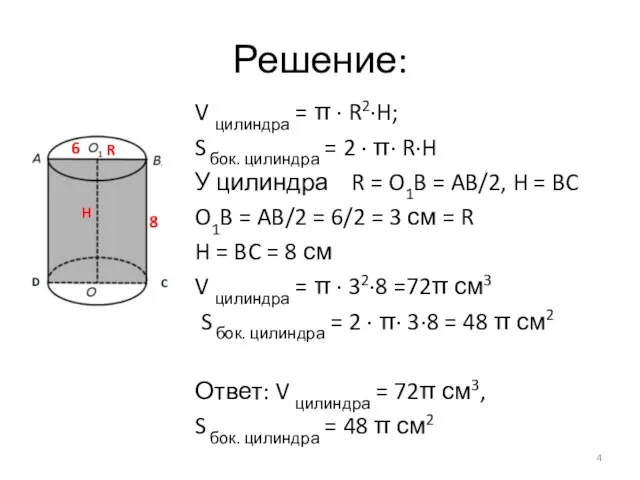
- 4. Решение: V цилиндра = π · R2·H; S бок. цилиндра = 2 · π· R·H У
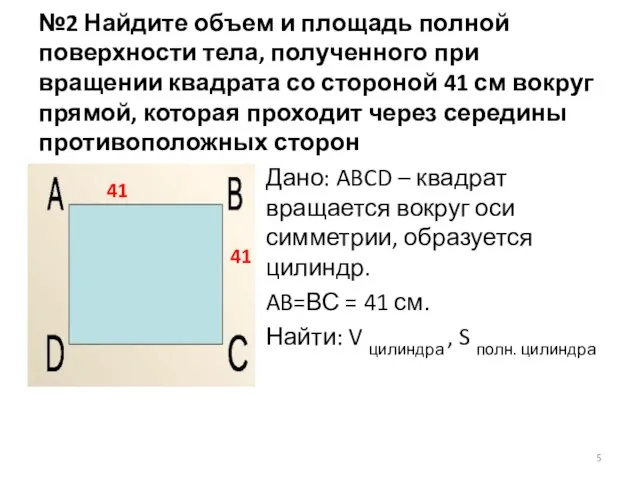
- 5. №2 Найдите объем и площадь полной поверхности тела, полученного при вращении квадрата со стороной 41 см
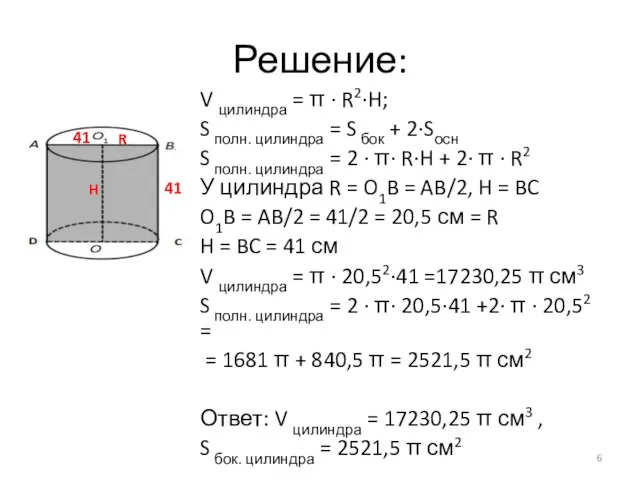
- 6. Решение: V цилиндра = π · R2·H; S полн. цилиндра = S бок + 2·Sосн S
- 7. Практическая работа Вариант В=20 В – 2 последние цифры по студенческому билету №1 Найдите объем и
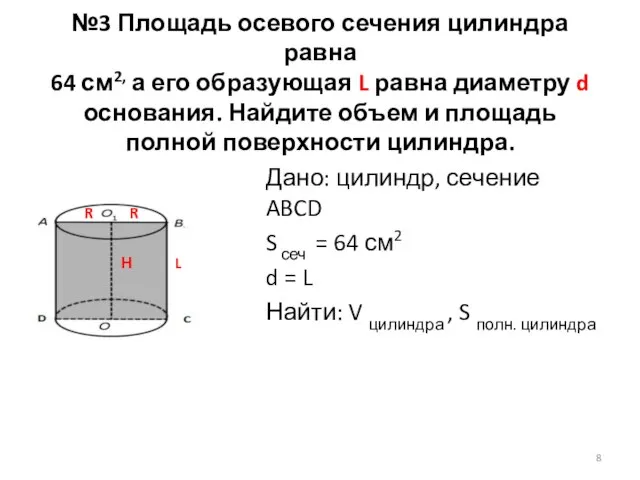
- 8. №3 Площадь осевого сечения цилиндра равна 64 см2, а его образующая L равна диаметру d основания.
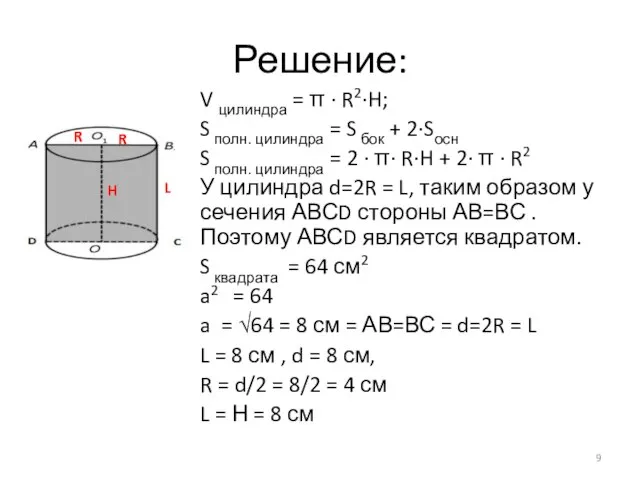
- 9. Решение: V цилиндра = π · R2·H; S полн. цилиндра = S бок + 2·Sосн S
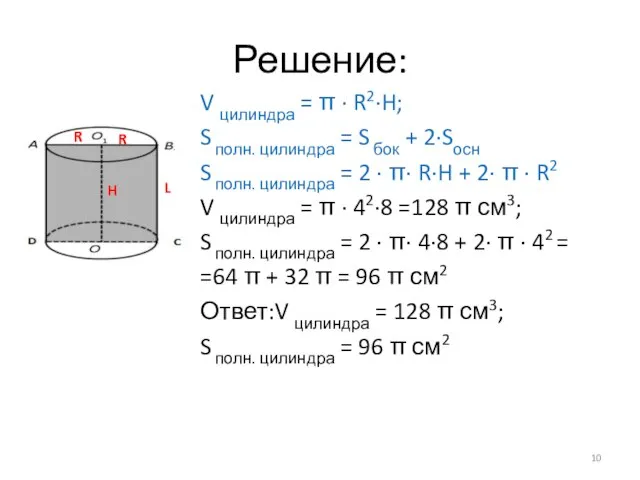
- 10. Решение: V цилиндра = π · R2·H; S полн. цилиндра = S бок + 2·Sосн S
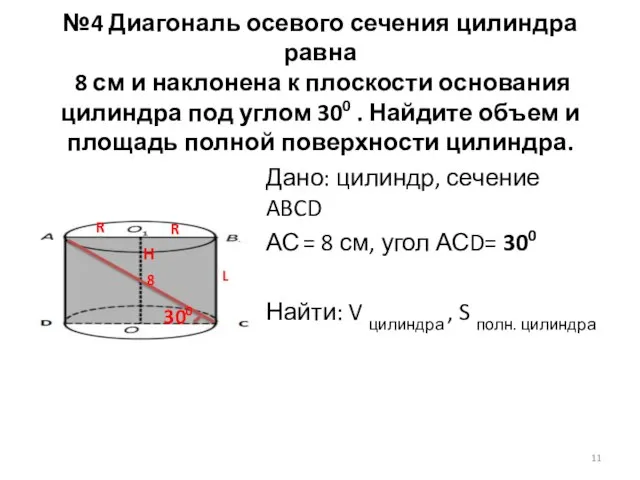
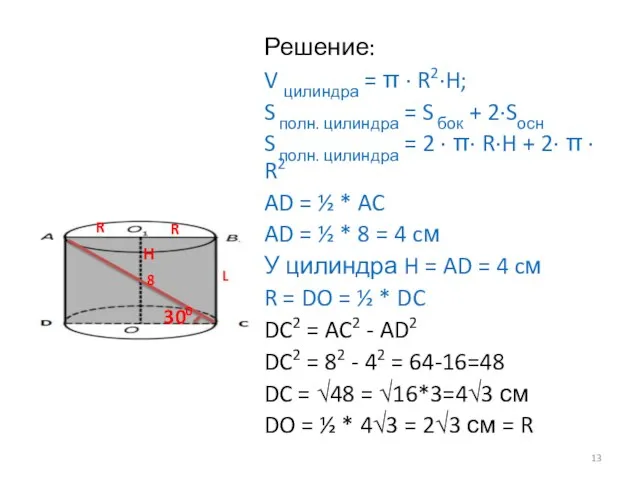
- 11. №4 Диагональ осевого сечения цилиндра равна 8 см и наклонена к плоскости основания цилиндра под углом
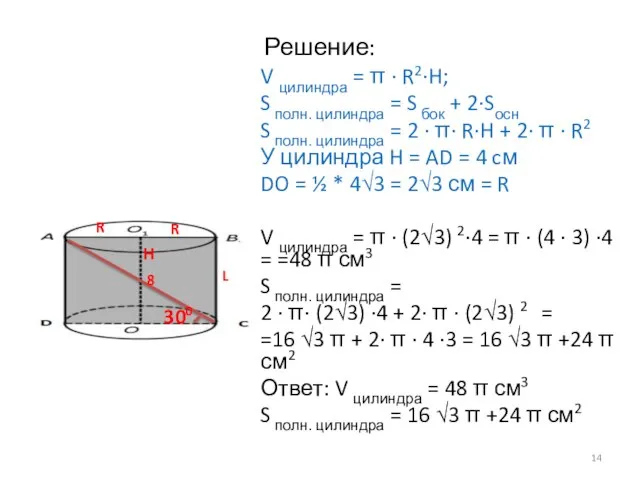
- 12. Решение: V цилиндра = π · R2·H; S полн. цилиндра = S бок + 2·Sосн S
- 13. Решение: V цилиндра = π · R2·H; S полн. цилиндра = S бок + 2·Sосн S
- 14. Решение: V цилиндра = π · R2·H; S полн. цилиндра = S бок + 2·Sосн S
- 15. Самостоятельная работа Вариант В=20 №3 Площадь осевого сечения цилиндра равна В см2, а его образующая равна
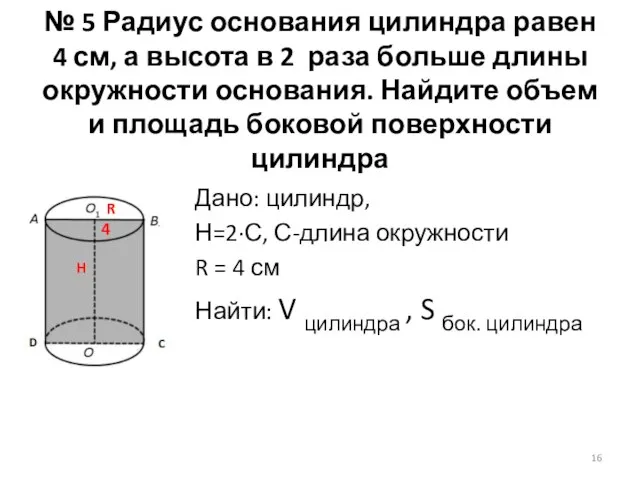
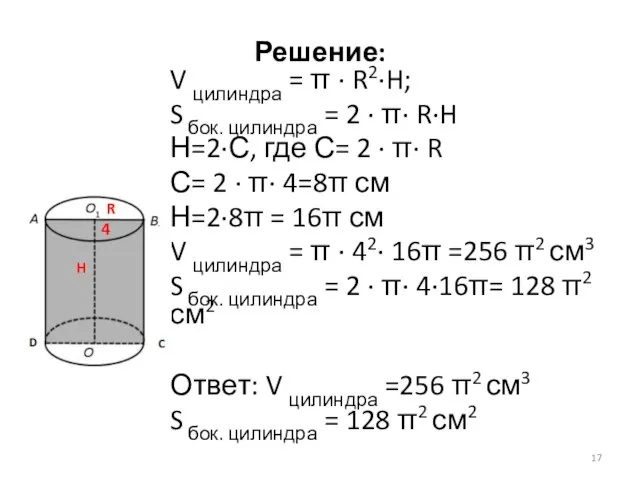
- 16. № 5 Радиус основания цилиндра равен 4 см, а высота в 2 раза больше длины окружности
- 17. Решение: V цилиндра = π · R2·H; S бок. цилиндра = 2 · π· R·H Н=2∙С,
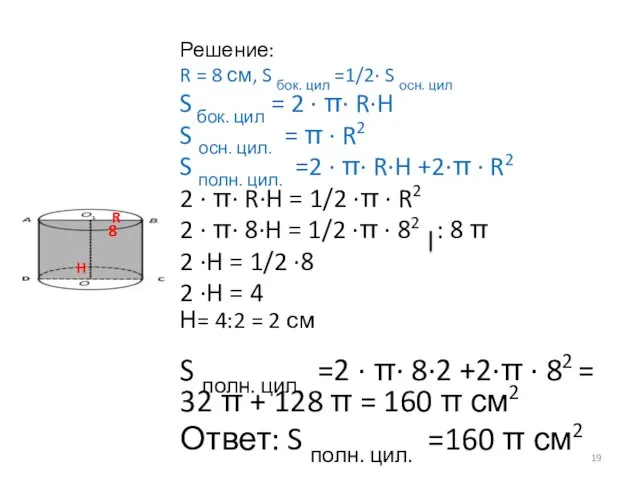
- 18. № 6 Радиус основания цилиндра равен 8 см, площадь боковой поверхности вдвое меньше площади основания. Найдите
- 19. Решение: R = 8 см, S бок. цил =1/2∙ S осн. цил S бок. цил =
- 20. Вариант В=20 № 5 Радиус основания цилиндра равен В0 см, а высота в 2 раза меньше
- 21. Площадь и объем шара. Площадь сечения шара. Решение задач.
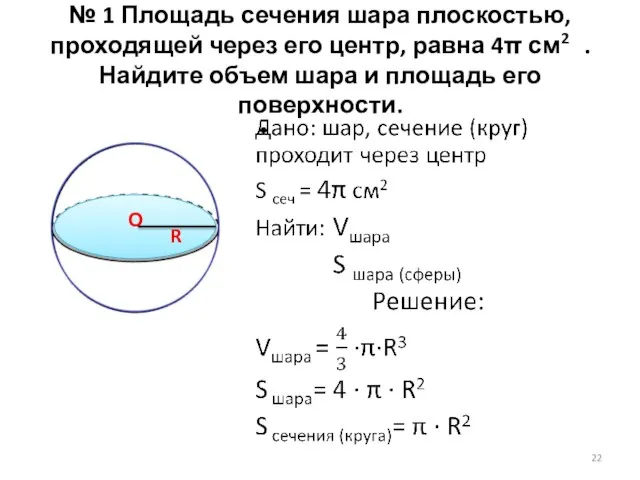
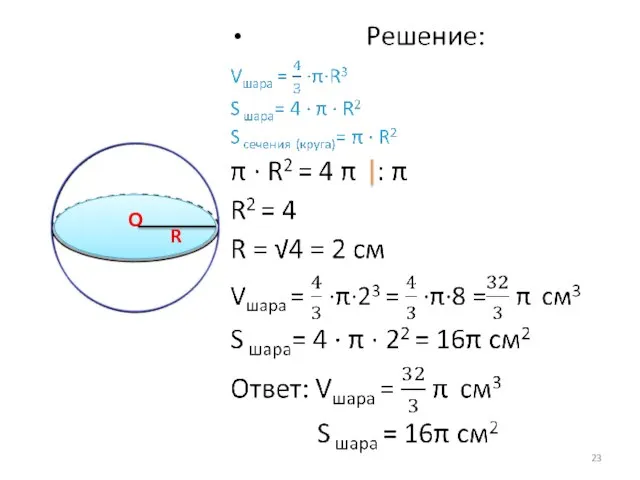
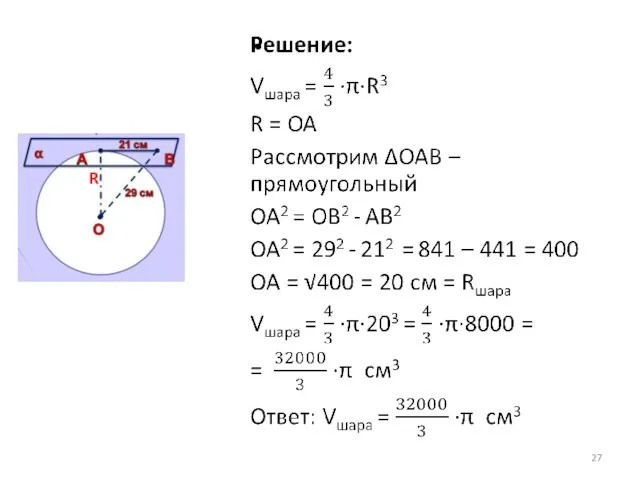
- 22. № 1 Площадь сечения шара плоскостью, проходящей через его центр, равна 4π см2 . Найдите объем
- 23. О R
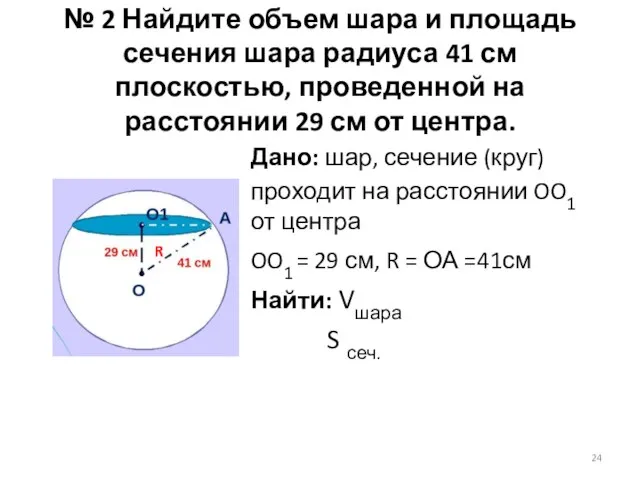
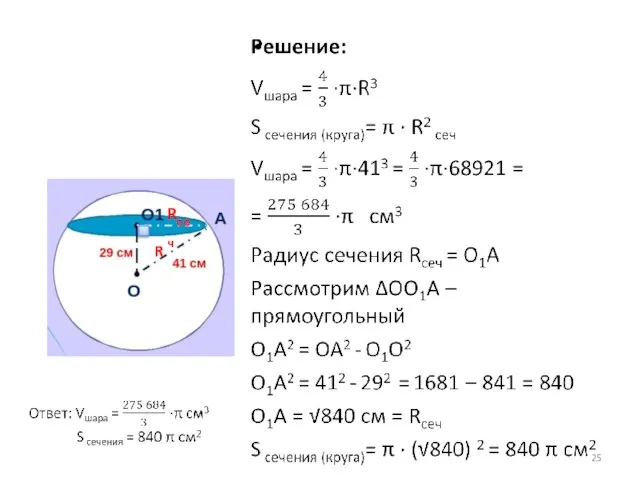
- 24. № 2 Найдите объем шара и площадь сечения шара радиуса 41 см плоскостью, проведенной на расстоянии
- 25. R Rсеч
- 26. № 3 Шар с центром в точке О касается плоскости в точке А. Точка В лежит
- 27. R R
- 29. Скачать презентацию








 Теорема Пифагора
Теорема Пифагора Вывод формулы Герона. Геометрия 8 класс
Вывод формулы Герона. Геометрия 8 класс Coordinate plane
Coordinate plane Шар и сфера
Шар и сфера Применение производной
Применение производной Помогают законы. 5 - 7 класс
Помогают законы. 5 - 7 класс Многоугольник
Многоугольник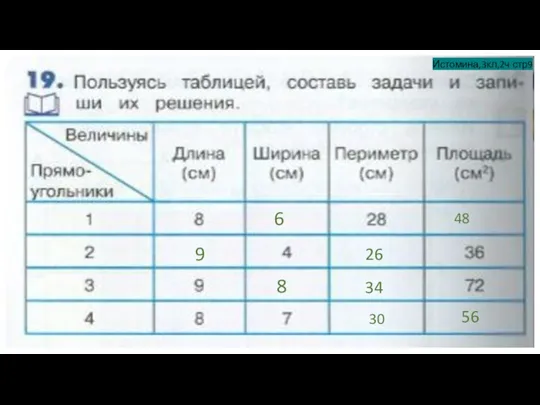 Величины. Составление задач
Величины. Составление задач Математика для дошкольников (средняя группа)
Математика для дошкольников (средняя группа) Кто живет под грибом
Кто живет под грибом Задачи для практики
Задачи для практики Введение в геометрию
Введение в геометрию Логическая задача. Способы решения
Логическая задача. Способы решения Презентация по математике "Величины. Объём" -
Презентация по математике "Величины. Объём" -  Презентация на тему Волейбол. Передача сверху
Презентация на тему Волейбол. Передача сверху  Алгебраическая дробь и её основное свойство. 7 класс
Алгебраическая дробь и её основное свойство. 7 класс Задачи на расстояния в пространстве
Задачи на расстояния в пространстве Как умножали египтяне
Как умножали египтяне Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Презентация по математике "Число 7" -
Презентация по математике "Число 7" -  Симметрия в геометрии и в жизни
Симметрия в геометрии и в жизни Классификация функций
Классификация функций Математика
Математика Показательное уравнение
Показательное уравнение Алгебра. Дроби. Сумма дробей
Алгебра. Дроби. Сумма дробей Координатная плоскость
Координатная плоскость Чётность и не чётность тригонометрических функций
Чётность и не чётность тригонометрических функций Числовая последовательность
Числовая последовательность