Содержание
- 2. Лекция 3
- 3. Формула классической вероятности , где m – число элементарных исходов, благоприятствующих А; n – число всех
- 4. Свойства вероятности Свойство 1. Вероятность достоверного события равна единице.
- 5. Свойство 2. Вероятность невозможного события равна нулю.
- 6. Свойство 3. Вероятность случайного события А есть число, заключенное между нулем и единицей.
- 7. Требования к классической схеме 1) Выбрать множество элементарных исходов 2)Подсчитать число всех элементарных исходов 3)Если вычисляем
- 8. Пример 1 Монету подбрасывают дважды. Построить множество элементарных исходов.
- 9. Решение Если учитывать порядок, то исходов получится четыре (герб,герб) (решка,решка) (герб,решка) (решка,герб) Все эти исходы равновозможны.
- 10. Если порядок не учитывать, то исходы (решка,герб) и (герб,решка) считают как один. Тогда элементарных исходов будет
- 11. Гипергеометрическая формула
- 12. В случае разбиения исходного множества на два подмножества
- 13. N – общее количество элементов M – количество элементов определенного типа n – отобранные m –
- 14. Пример 1 В фирме работают 6 женщин и 4 мужчин. Наудачу отобраны 7 человек. Чему равна
- 15. Пример 2 В партии из 6 деталей 3 стандартных. Найти вероятность того, что среди четырех взятых
- 16. Покерные комбинации Пара(2) :Т♠;10♣;К♣;2♦;2♠ Две пары:(2+2) 10♠;10♣;К♣;2♦;2♠ Тройка(3): Т♠;10♣;2♣;2♦;2♠ Стрит(Street): Т♠;10♣;К♣;Д♦;В♥ Флеш(Flush): Т♠;10 ♠;К ♠;2 ♠;2♠
- 17. Расчет вероятностей покерных комбинаций Результат эксперимента – наименования пяти карт, например, (Т♠;10♣;К♣;2♦;2♠). Число всех исходов
- 18. Вероятность пары Число благоприятных исходов и вероятность пары
- 19. Вероятность двух пар Число благоприятных исходов и вероятность двух пар
- 21. Относительная частота Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу
- 22. Пример По цели произвели 32 выстрела, причем было зарегистрировано 15 попаданий. Чему равна относительная частота поражения
- 23. Статистическая вероятность появления события Относительная частота –приближенное значение вероятности, называемое статистической.
- 24. Пример По данным статистики, относительная частота рождения девочек за некоторый год по месяцам характеризуется следующими числами
- 25. Относительная частота колеблется около числа 0,482, которое можно принять за приближенное значение вероятности рождения девочек.
- 26. Проверка свойств статистической вероятности 1. Если событие достоверно, то m = n и относительная частота 2.
- 27. Для любого события , и, следовательно, относительная частота , т.е. статистическая вероятность любого события заключена между
- 28. Операции над событиями
- 29. Сумма событий Пусть даны события А и В. Сумма событий А+В – событие, которое означает, что
- 30. Разность событий Разностью двух событий A-B называется событие, состоящее в том, что А произошло, но В
- 31. Произведение событий Пусть даны события А и В. Произведение событий АВ – событие, которое означает, что
- 32. Противоположные события и События называются противоположными, если они несовместны и образуют полную группу.
- 33. Другими словами: Событием, противоположным к А, называется событие Ā, состоящее в том, что событие А не
- 34. Примеры А={идет дождь} В={идет снег} АВ={идет дождь и снег} А+В={идет дождь или снег}
- 35. Пример противоположного события = {попадание в мишень} = {промах}
- 36. Задача 1 Вероятность того, что день будет ясным равна 0,3. Чему равна вероятность, что день будет
- 37. Задача 2 Вероятность не сдать зачет по предмету для некоторого студента равна 0,8. Какова вероятность сдать
- 38. Решение Обозначим событие A={сдать зачет}. Тогда противоположным событием будет событие Ā={не сдать зачет}. Так как P(A)+P(Ā)=1,
- 39. Вероятностное пространство
- 40. Пусть в результате испытания наступает одно и только одно из совокупности событий, называемых элементарными событиями (элементарными
- 41. Множество всех элементарных событий, которые могут появиться в испытании, называют пространством элементарных событий , а сами
- 42. Пример В урне 4 шара: красный, синий, желтый, зеленый. Наудачу вынимают один шар. Выпишем множество элементарных
- 43. Пространство Точки этого пространства
- 44. Поле событий S Поле событий – подмножество множества всех подмножеств , замкнутое относительно операций объединения, пересечения,
- 45. Аксиомы вероятностного пространства: 1. Каждому событию А поставлено в соответствие неотрицательное действительное число Р (А). Это
- 46. Вероятностное пространство
- 47. Типы пространств Выделяют два основных типа: Дискретное вероятностное пространство; Непрерывное вероятностное пространство.
- 48. Дискретное вероятностное пространство Конечное – классическая схема; неклассическая. Бесконечное.
- 49. Непрерывное пространство Пример. Случайный эксперимент – измерение роста человека. Случайное событие – произвольное положительное действительное число.
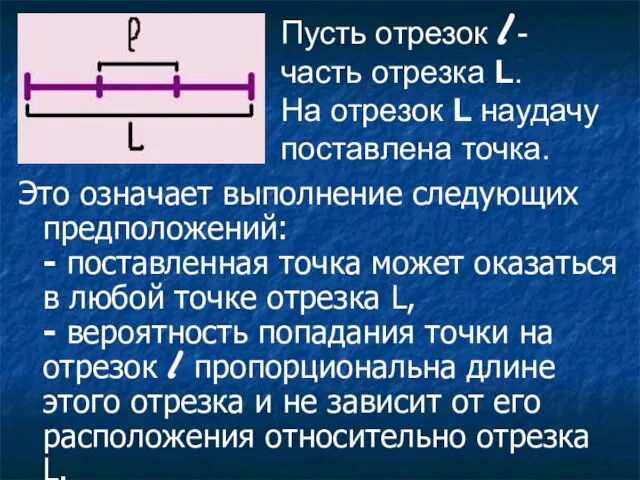
- 50. Геометрические вероятности Геометрические вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т.д.).
- 51. Это означает выполнение следующих предположений: - поставленная точка может оказаться в любой точке отрезка L, -
- 52. Вероятность попадания точки на отрезок l определяется равенством
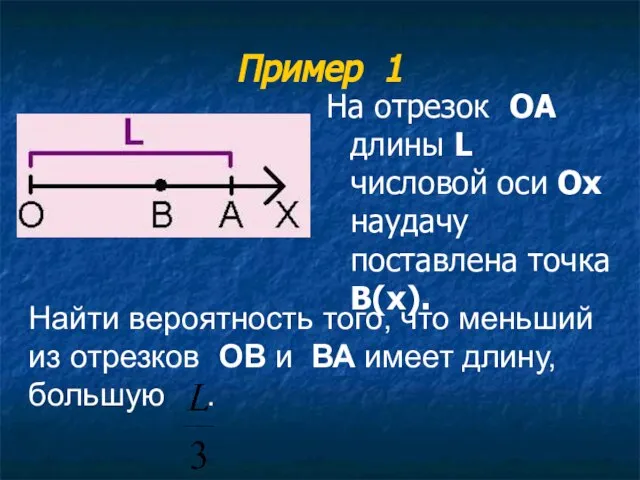
- 53. Пример 1 На отрезок ОА длины L числовой оси Ох наудачу поставлена точка В(х). Найти вероятность
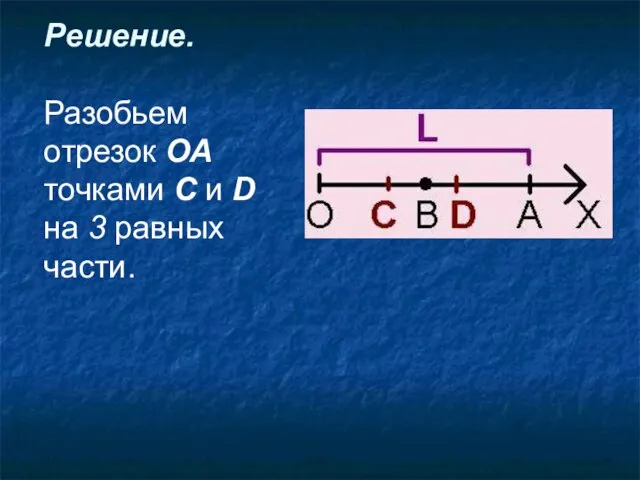
- 54. Решение. Разобьем отрезок ОА точками С и D на 3 равных части.
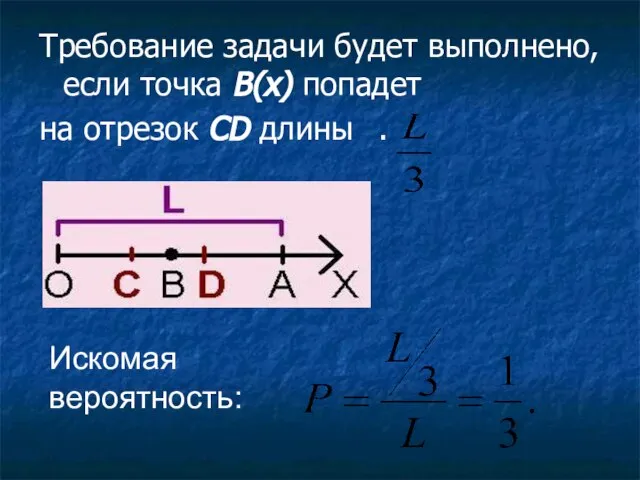
- 55. Требование задачи будет выполнено, если точка В(х) попадет на отрезок CD длины . Искомая вероятность:
- 56. Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка.
- 57. Вероятность попадания точки в фигуру g определяется равенством:
- 58. Пример 2 На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти
- 59. Решение. Площадь кольца (фигуры g):
- 60. Площадь большого круга (фигуры G): Искомая вероятность:
- 61. Замечание В случае классического определения вероятность достоверного (невозможного) события равна единице (нулю); справедливы и обратные утверждения
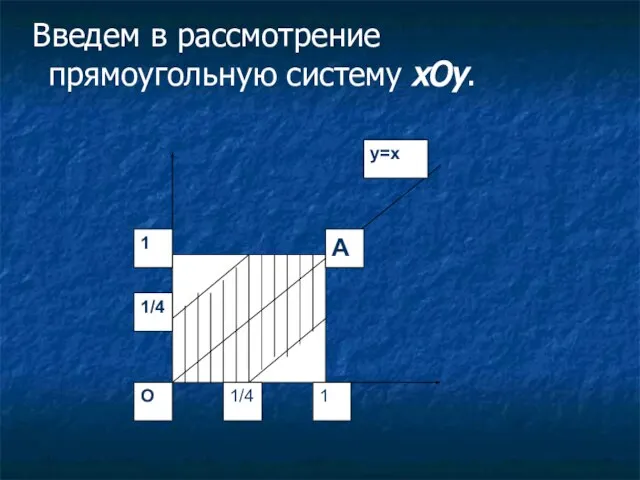
- 62. Задача о встрече Два человека договорились встретится в течение часа, причем время ожидания первым относительно второго
- 63. Решение. Обозначим моменты прихода первого и второго соответственно через x и y. В силу условия задачи
- 64. Введем в рассмотрение прямоугольную систему xOy.
- 65. Таким образом,
- 66. Задачи
- 67. Задача 1 В прямоугольник 5x4 см2 вписан круг радиуса 1,5 см. Какова вероятность того, что точка,
- 68. Решение По определению геометрической вероятности искомая вероятность равна отношению площади круга (в который точка должна попасть)
- 69. Задача 2 В квадрат со стороной 6 вписан круг. Наудачу в квадрат бросают точку. Найти вероятность,
- 70. Решение По определению геометрической вероятности искомая вероятность равна отношению площади квадрата к площади круга Площадь квадрата
- 71. Заметим, что радиус вписанного в квадрат круга будет равен половине стороны квадрата, R=3 Площадь круга с
- 72. Вопросы к лекции 3 Напишите гипергеометричекую формулу Что называют относительной частотой? Что такое статистическая вероятность? Сумма
- 74. Скачать презентацию


































































 Пропорции. Задачи
Пропорции. Задачи Презентация на тему Движение
Презентация на тему Движение  Сложение и вычитание числа 2
Сложение и вычитание числа 2 Математика
Математика Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ  Математика и спорт
Математика и спорт Разложение вектора по трём некомпланарным векторам
Разложение вектора по трём некомпланарным векторам Десятки, единицы, цифры
Десятки, единицы, цифры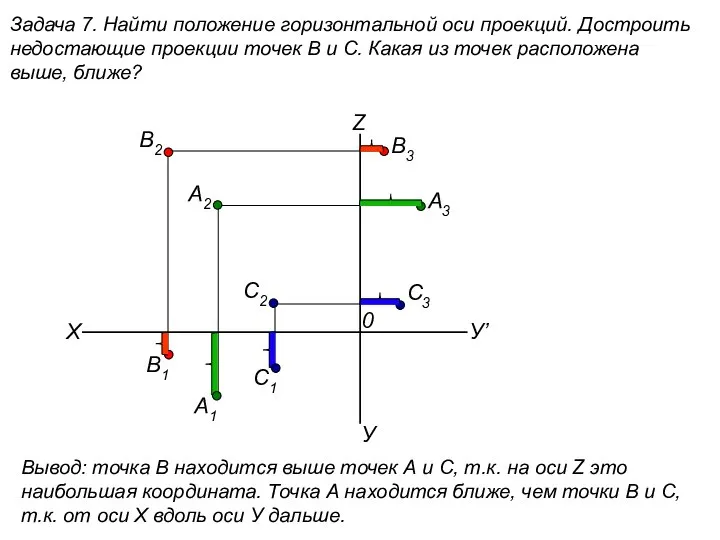 Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7)
Найти положение горизонтальной оси проекций. Достроить недостающие проекции точек В и С. (задача 7) Уравнение касательной к графику функции
Уравнение касательной к графику функции Решение уравнений. Первый и второй уровни
Решение уравнений. Первый и второй уровни Предельные величины, эластичности
Предельные величины, эластичности Математика – наука о наиболее общих и фундаментальных структурах реального мира
Математика – наука о наиболее общих и фундаментальных структурах реального мира Практическое применение треугольников в жизни
Практическое применение треугольников в жизни Освоение основных универсальных предметных знаний и умений в курсе технологии
Освоение основных универсальных предметных знаний и умений в курсе технологии Ряды динамики
Ряды динамики Презентация по математике "Знакомство с занимательной литературой по математике" -
Презентация по математике "Знакомство с занимательной литературой по математике" -  Простейшие функции и их графики
Простейшие функции и их графики Решение тригонометрических уравнений
Решение тригонометрических уравнений Логарифмические уравнения
Логарифмические уравнения Занимательные задачи
Занимательные задачи Комбинаторика
Комбинаторика Площадь параллелограмма. 8 класс
Площадь параллелограмма. 8 класс Соста числа 11
Соста числа 11 Обратные тригонометрические функции
Обратные тригонометрические функции Десятичный и натуральный логарифм
Десятичный и натуральный логарифм Параллельный перенос
Параллельный перенос Геймификация образовательного процесса на уроках математики с использованием двигательной активности
Геймификация образовательного процесса на уроках математики с использованием двигательной активности