Пирамида. Площадь поверхности пирамиды

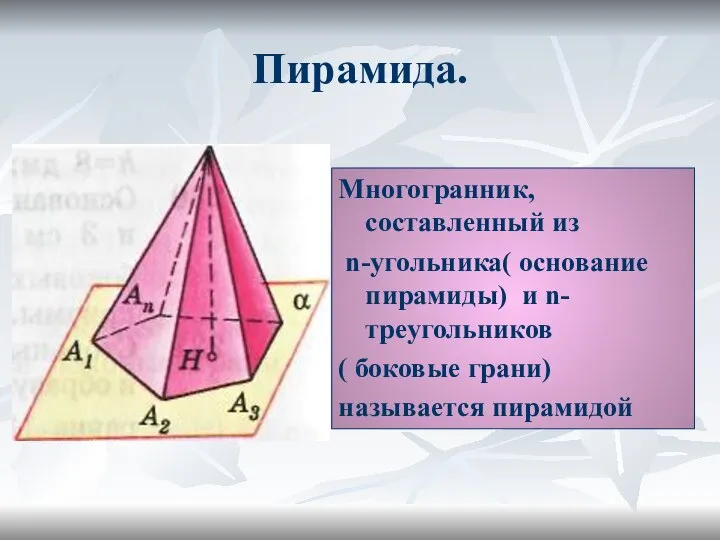
Пирамида.
Многогранник, составленный из
n-угольника( основание пирамиды) и n-треугольников
( боковые грани)
называется пирамидой

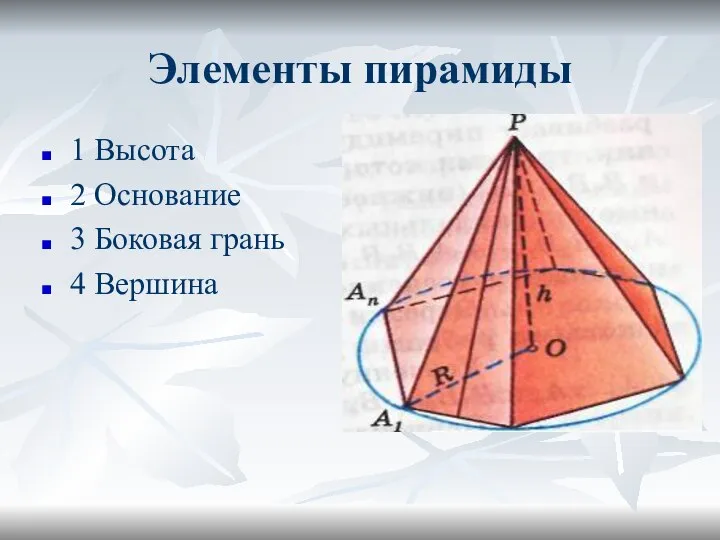
Элементы пирамиды
1 Высота
2 Основание
3 Боковая грань
4 Вершина

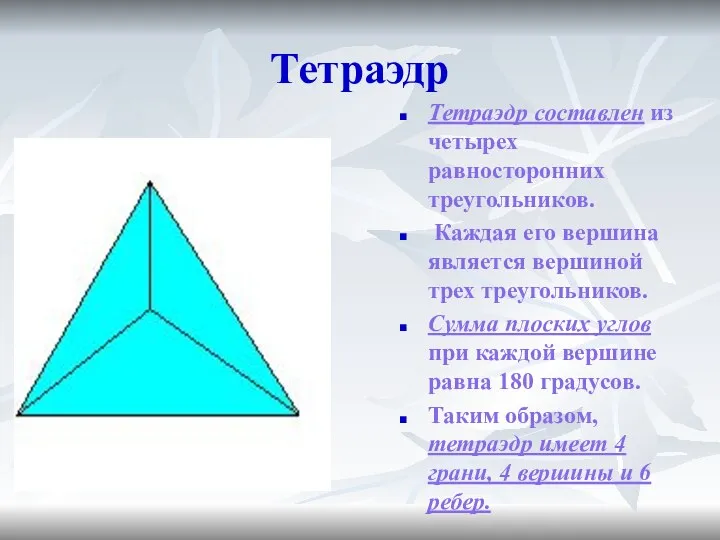
Тетраэдр
Тетраэдр составлен из четырех равносторонних треугольников.
Каждая его вершина является вершиной трех треугольников.
Сумма плоских углов при каждой вершине равна 180 градусов.
Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.

Правильная пирамида
Пирамида называется правильной, если ее основание- правильный многоугольник и вершина пирамиды проектируется в центр основания.
В правильной пирамиде:
все боковые ребра равны,
все боковые грани- равные равнобедренные треугольники,
все ее боковые ребра образуют с плоскостью
основания равные углы.

Высота боковой грани правильной пирамиды, проведенной к ребру ее основания, называется апофемой.
Все апофемы правильной пирамиды равны.

Площадь боковой и полной поверхности пирамиды
Площадь полной поверхности пирамиды равна сумме площадей ее боковой поверхности и основания.
Sпол= Sбок+Sосн
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему пирамиды
Sбок = ½ Pl
Объём пирамиды равен одной трети произведения площади основания на высоту.
V=⅓SH

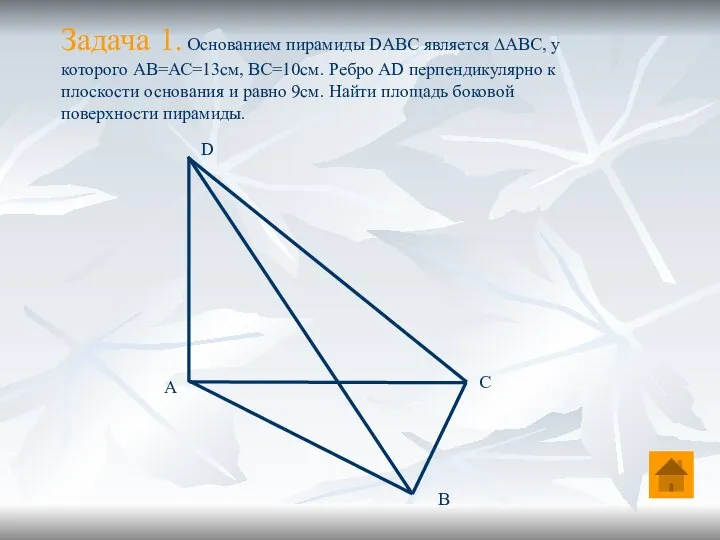
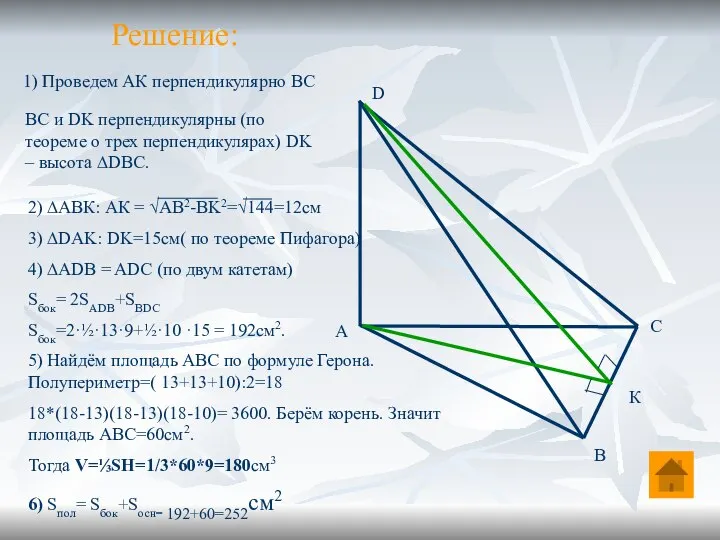
Задача 1. Основанием пирамиды DABC является ∆АВС, у которого АВ=АС=13см, ВС=10см. Ребро АD перпендикулярно к плоскости основания и равно 9см. Найти площадь боковой поверхности пирамиды.
А
В
С
D

Решение:
А
С
D
В
1) Проведем АК перпендикулярно ВС
К
ВС и DK перпендикулярны (по теореме о трех перпендикулярах) DK – высота ∆DBC.
2) ∆АВК: АК = √АВ2-BK2=√144=12см
3) ∆DAK: DK=15см( по теореме Пифагора)
4) ∆ADB = ADC (по двум катетам)
Sбок= 2SADB+SBDC
Sбок=2·½·13·9+½·10 ·15 = 192см2.
5) Найдём площадь АВС по формуле Герона. Полупериметр=( 13+13+10):2=18
18*(18-13)(18-13)(18-10)= 3600. Берём корень. Значит площадь АВС=60см2.
Тогда V=⅓SH=1/3*60*9=180см3
6) Sпол= Sбок+Sосн= 192+60=252см2