Содержание
- 2. Математические кривые в повседневной жизни Проект выполнили: Чежегов Александр, Мартьянов Иван, 8 класс МБОУ ФМЛ г.
- 3. Цель работы – создать анимационные модели графиков (параболы, синусоиды, циклоиды, архимедовой и логарифмической спиралей). Задачи проекта:
- 4. Вся анимация сделана авторами проекта и не имеет аналогов. Это: gif-анимация на основе фото и рисунков,
- 5. парабола синусоида циклоида архимедова спираль логарифмическая спираль Приложение 1 Приложение 2 Приложение 3
- 6. Парабола y = ax 2 + bx + c
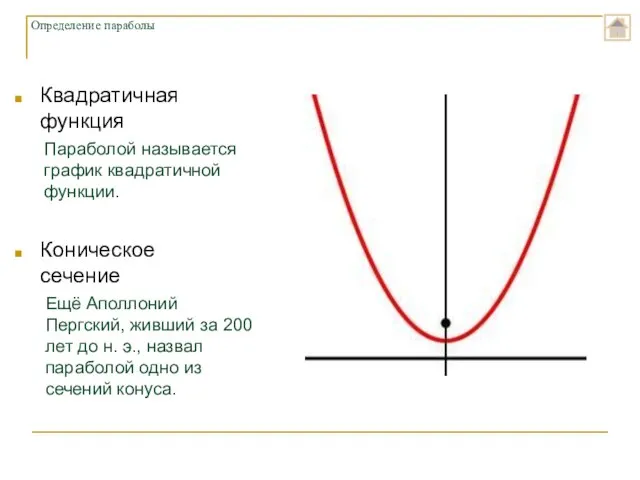
- 7. Определение параболы Квадратичная функция Коническое сечение Параболой называется график квадратичной функции. Ещё Аполлоний Пергский, живший за
- 8. Свойства параболы Свободное падение Действие атмосферы Струя и гравитация Любой предмет, брошенный под углом к горизонту,
- 9. Модель параболы Баллистика Прыжок В баллистике часто используется закон полета тела по параболе. Известно, что траектория
- 10. Синусоида y = a + b sin(cx + d)
- 11. Движение змеи Волны жидкости Прогиб опоры Виды волн Биение сердца Синусоиду часто можно видеть в рисунках,
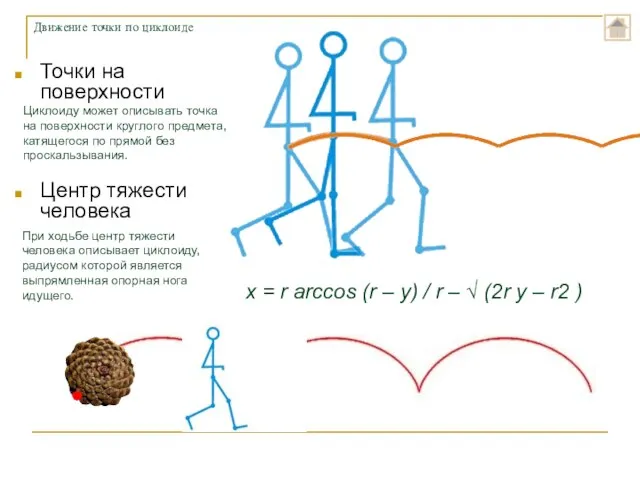
- 12. Циклоида x = r arccos (r – y) / r – √ (2r y – r2
- 13. Точки на поверхности Центр тяжести человека Движение точки по циклоиде Циклоиду может описывать точка на поверхности
- 14. Кривая кратчайшего спуска Таутохрона Свойства циклоиды Среди многих замечательных свойств циклоиды отметим одно, из-за которого она
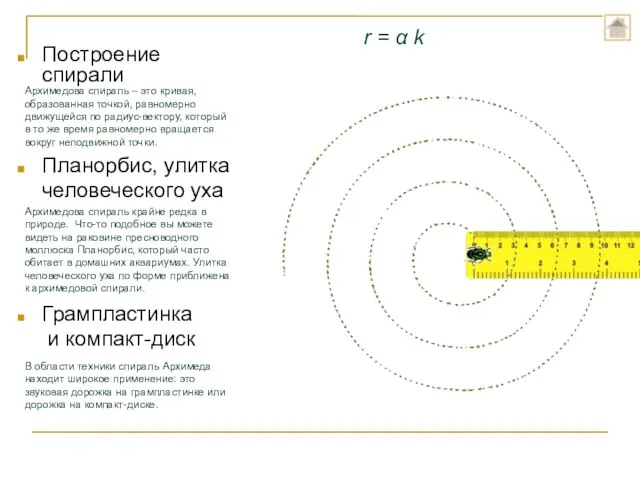
- 15. Архимедова спираль r = α k
- 16. Построение спирали Планорбис, улитка человеческого уха Грампластинка и компакт-диск Архимедова спираль – это кривая, образованная точкой,
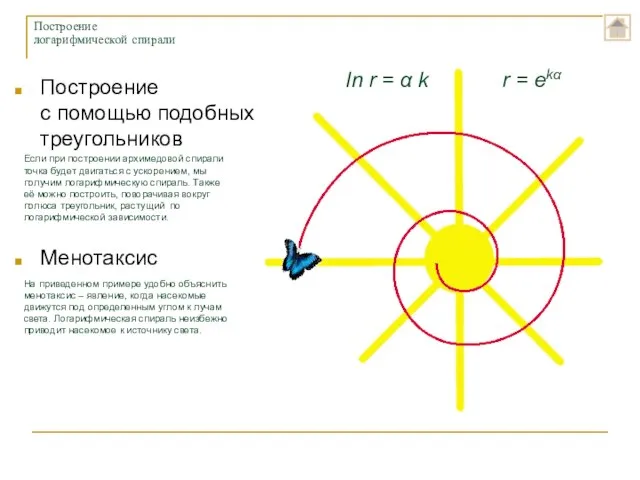
- 17. Логарифмическая спираль ln r = α k
- 18. Построение с помощью подобных треугольников Менотаксис Построение логарифмической спирали Если при построении архимедовой спирали точка будет
- 19. Раковина аммонита, рога архара Подсолнух, ананас, шишка Циклоны, водовороты, смерчи Примеры логарифмической спирали Раковины и рога
- 20. Маленькие и большие логарифмические спирали Самой маленькой аэродинамической спиралью можно считать микроторнадо, которое создает кленовое семя,
- 21. В природе траектории тел, их деформация и рост связаны с математическими кривыми. Кривые используются в технике.
- 22. Приложение 1. Примеры кривых в быту Посмотрите на сделанные нами снимки. Какие кривые вы на них
- 23. Гюйгенс нашел так называемую таутохрону, т.е. кривую, по которой тела скатываются вниз за одно и то
- 25. Скачать презентацию




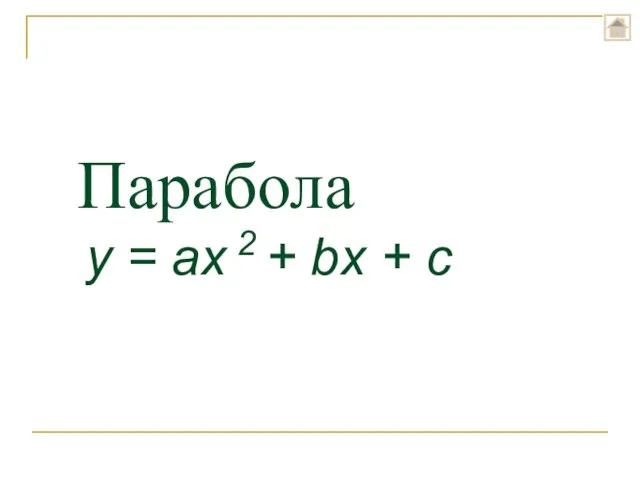


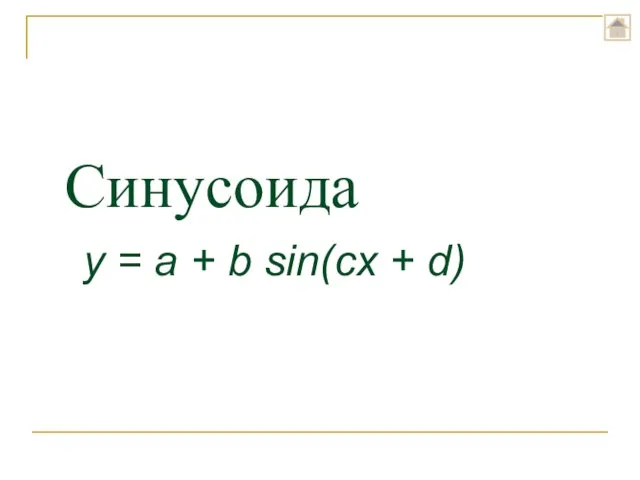










 Kombinatorika
Kombinatorika Задачи на проценты
Задачи на проценты Презентация
Презентация Математические головоломки. Математика вокруг нас
Математические головоломки. Математика вокруг нас Периметр и площадь прямоугольника. Подготовка к контрольной работе
Периметр и площадь прямоугольника. Подготовка к контрольной работе Векторы. Линейные операции над векторами. Разложение вектора по базису
Векторы. Линейные операции над векторами. Разложение вектора по базису Отношение чисел
Отношение чисел Лекция 20
Лекция 20 Домашнее задание по геометрии
Домашнее задание по геометрии Матрицы и действия над ними
Матрицы и действия над ними Итоговая контрольная работа
Итоговая контрольная работа Теорема Пифагора
Теорема Пифагора Умножение на 1. Проведите динозаврика по лабиринту (1)
Умножение на 1. Проведите динозаврика по лабиринту (1) Презентация на тему РЕШЕНИЕ УРАВНЕНИЙ С МОДУЛЕМ
Презентация на тему РЕШЕНИЕ УРАВНЕНИЙ С МОДУЛЕМ  Основы логистики
Основы логистики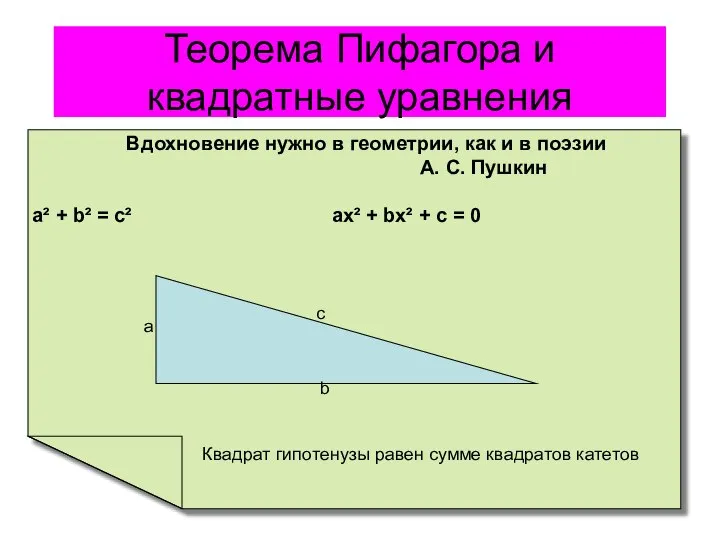 Теорема Пифагора и квадратные уравнения
Теорема Пифагора и квадратные уравнения Окружность, круг, их элементы и части. Центральный угол
Окружность, круг, их элементы и части. Центральный угол Плоскость. Прямая. Луч
Плоскость. Прямая. Луч Твёрдые и мягкие согласные звуки. Сложение и вычитание без перехода через десяток
Твёрдые и мягкие согласные звуки. Сложение и вычитание без перехода через десяток Построение графиков функций
Построение графиков функций 1_1_matritsy (1)
1_1_matritsy (1) Юность Великих математиков. 5 класс
Юность Великих математиков. 5 класс Симметрия
Симметрия Повелеваю в моем сказочном Математическом королевстве ребятам 1-в класса
Повелеваю в моем сказочном Математическом королевстве ребятам 1-в класса Математические ребусы
Математические ребусы Математика без границ. Конкурс
Математика без границ. Конкурс Решение задач по теме: Двумерный массив. Профильный уровень
Решение задач по теме: Двумерный массив. Профильный уровень Изучить понятия параллельное проектирование и его
Изучить понятия параллельное проектирование и его