Содержание
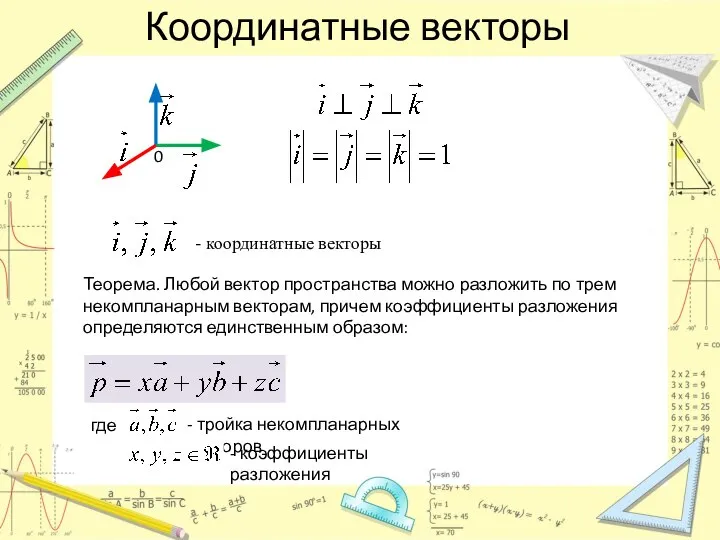
- 2. Координатные векторы 0 - координатные векторы Теорема. Любой вектор пространства можно разложить по трем некомпланарным векторам,
- 3. Координаты вектора В качестве тройки некомпланарных векторов, по которым производится разложение произвольного вектора, удобно выбрать координатные
- 4. Координаты вектора Координаты вектора равны коэффициентам разложения этого вектора по координатным векторам, т.е. Например: ?????
- 5. Действия с векторами в координатах Пусть даны Тогда:
- 6. Действия с векторами в координатах Пусть даны Найти координаты вектора Решение: Ответ:
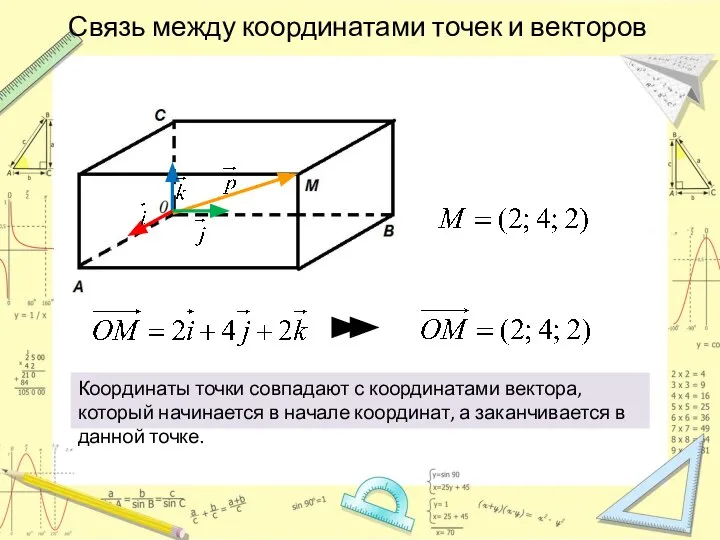
- 7. Связь между координатами точек и векторов Координаты точки совпадают с координатами вектора, который начинается в начале
- 9. Скачать презентацию




 Методы и приемы реализации математических моделей теплотехнических систем макроуровня (продолжение)
Методы и приемы реализации математических моделей теплотехнических систем макроуровня (продолжение) Рыцарский турнир
Рыцарский турнир Натуральные и целые числа, арифметические действия над ними
Натуральные и целые числа, арифметические действия над ними Понятие площади. Площадь квадрата и прямоугольника
Понятие площади. Площадь квадрата и прямоугольника Координаты вектора
Координаты вектора Квадратичная функция и ее свойства
Квадратичная функция и ее свойства Решение задач
Решение задач Логическая задача со спичками
Логическая задача со спичками Движения. 9-й класс
Движения. 9-й класс Презентация на тему Возведение в степень произведения и степени (7 класс)
Презентация на тему Возведение в степень произведения и степени (7 класс)  Распределение Максвелла
Распределение Максвелла Прямоугольник, его свойства и признаки
Прямоугольник, его свойства и признаки Выражения. Подготовка к ЕГЭ. Задачи
Выражения. Подготовка к ЕГЭ. Задачи Основные понятия и определения метрологии. Лекция 1
Основные понятия и определения метрологии. Лекция 1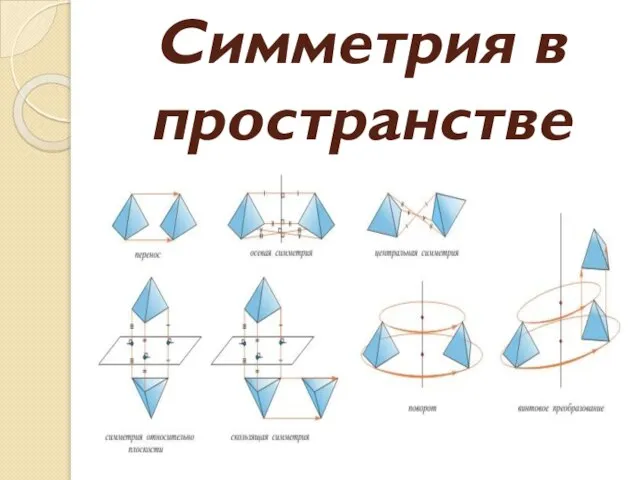 Симметрия в пространстве
Симметрия в пространстве Доказательство равносильностей
Доказательство равносильностей Разложение многочлена на множители с помощью формулы сокращенного умножения
Разложение многочлена на множители с помощью формулы сокращенного умножения Презентация по математике "Решение задач. Закрепление" -
Презентация по математике "Решение задач. Закрепление" -  Цилиндр. Урок математики
Цилиндр. Урок математики Операции, функции, выражения
Операции, функции, выражения День числа тау
День числа тау Умножение с опорным числом
Умножение с опорным числом Умножение на 0
Умножение на 0 Витамин В6: его формы, участие в рекакциях переаминирования и декарбоксилирования
Витамин В6: его формы, участие в рекакциях переаминирования и декарбоксилирования Вычисление производных с помощью правил дифференцирования
Вычисление производных с помощью правил дифференцирования Презентация на тему Пределы. Непрерывность функций
Презентация на тему Пределы. Непрерывность функций  Приёмы устных вычислений
Приёмы устных вычислений Средняя линия треугольника
Средняя линия треугольника