Содержание
- 2. Определение модуля Свойства модуля
- 3. Геометрический смысл модуля Геометрически есть расстояние от точки х числовой оси до начала отсчёта – точки
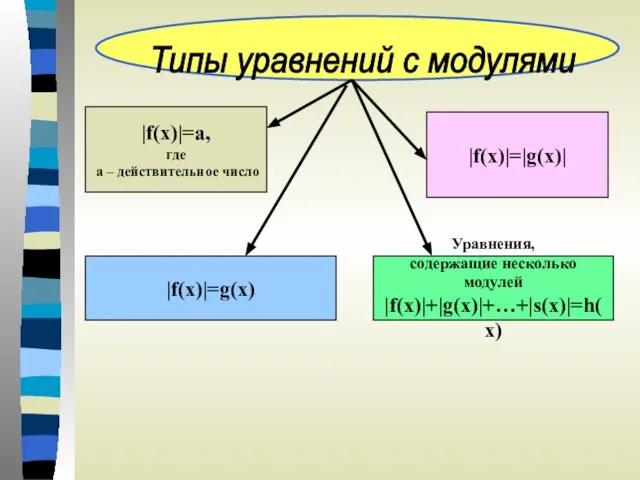
- 4. |f(x)|=a, где а – действительное число |f(x)|=g(x) |f(x)|=|g(x)| Уравнения, содержащие несколько модулей |f(x)|+|g(x)|+…+|s(x)|=h(x) Типы уравнений с
- 5. Решение уравнения |f(x)|=a Если а > 0, то f(x)=a f(x) = -a. 2) Если а=0, то
- 6. Решение уравнений |f(x)|=|g(x)|. |f(x)|=|g(x)|
- 7. Решение уравнений |f(x)|=g(x).
- 9. Скачать презентацию





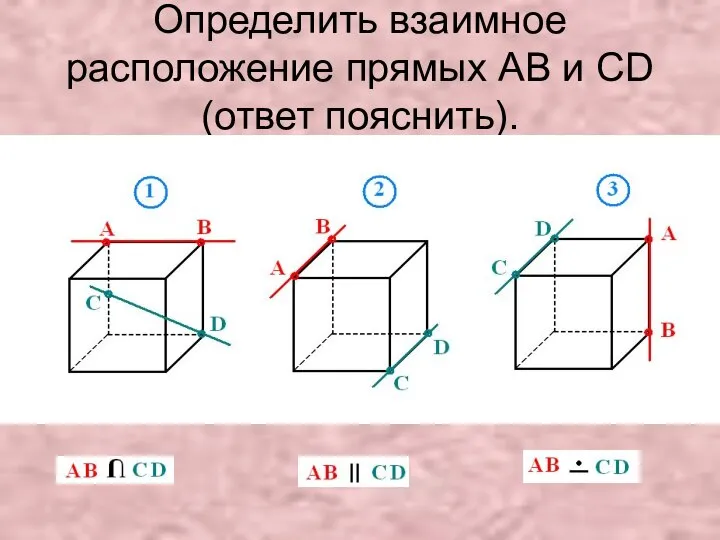 Прямая и плоскость в пространстве
Прямая и плоскость в пространстве Задачки со всего света. Проект Секреты чисел. Команда Искорка
Задачки со всего света. Проект Секреты чисел. Команда Искорка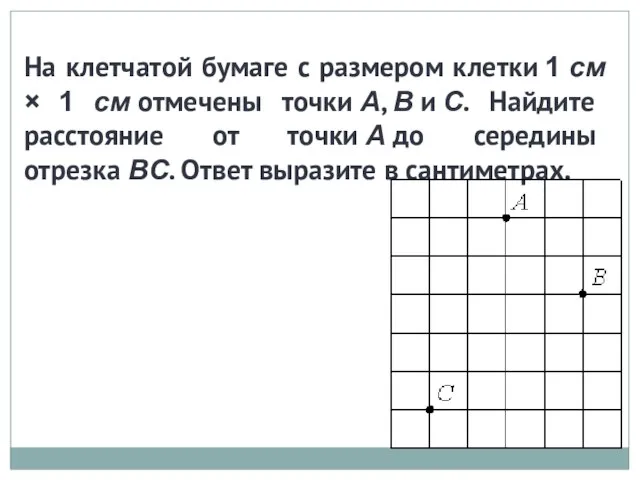 Решение задач
Решение задач Задания части 1. Вступительные испытания
Задания части 1. Вступительные испытания Презентация на тему Прототипы В12. Задачи на проценты
Презентация на тему Прототипы В12. Задачи на проценты  Сечения многогранников
Сечения многогранников Уравнение прямой. 9 класс
Уравнение прямой. 9 класс Цель: математическими способами доказать возможный вред курения
Цель: математическими способами доказать возможный вред курения Задания для устного счёта. 5 класс
Задания для устного счёта. 5 класс Задания по математике для 3 класса
Задания по математике для 3 класса Деление дробей. Растровая графика
Деление дробей. Растровая графика Путешествуем с теоремой Пифагора. 8 класс
Путешествуем с теоремой Пифагора. 8 класс Элементы комбинаторики
Элементы комбинаторики Параллельный перенос вдоль оси координат
Параллельный перенос вдоль оси координат Решение примеров в пределах 10
Решение примеров в пределах 10 Правильная треугольная усечённая пирамида
Правильная треугольная усечённая пирамида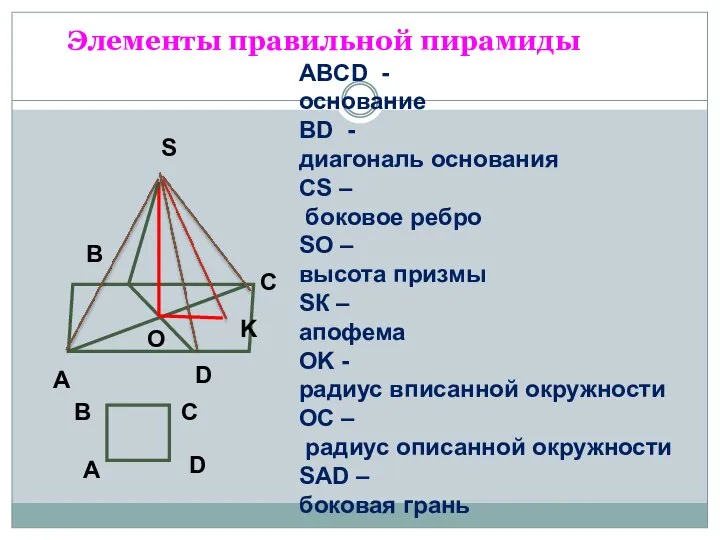 Правильная пирамида
Правильная пирамида Презентация на тему Случайные события и вероятность
Презентация на тему Случайные события и вероятность  Математическая азбука
Математическая азбука Оптико–геометрические иллюзии
Оптико–геометрические иллюзии Числовые великаны вокруг и внутри нас
Числовые великаны вокруг и внутри нас Перпендикуляр и наклонная к прямой
Перпендикуляр и наклонная к прямой Презентация на тему Сложение положительных и отрицательных чисел
Презентация на тему Сложение положительных и отрицательных чисел  Мішані числа
Мішані числа Презентация на тему Призма и ее свойства
Презентация на тему Призма и ее свойства  Алгебраические действия над комплексными числами
Алгебраические действия над комплексными числами Обобщающий урок по начертательной геометрии прямая. Плоскость
Обобщающий урок по начертательной геометрии прямая. Плоскость Обыкновенные дроби
Обыкновенные дроби