Содержание
- 2. Пример. Вычислить площадь фигуры, ограниченной линиями:
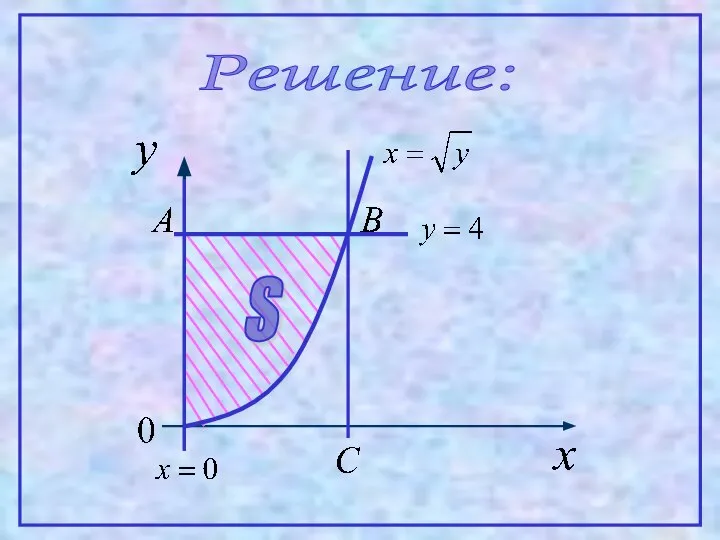
- 3. Решение: S
- 4. Находим координаты точки В: Тогда
- 5. 2 Пусть функция y=f(x) – неположительная и непрерывна на [a,b]. Отражая кривую y=f(x) относительно оси абсцисс,
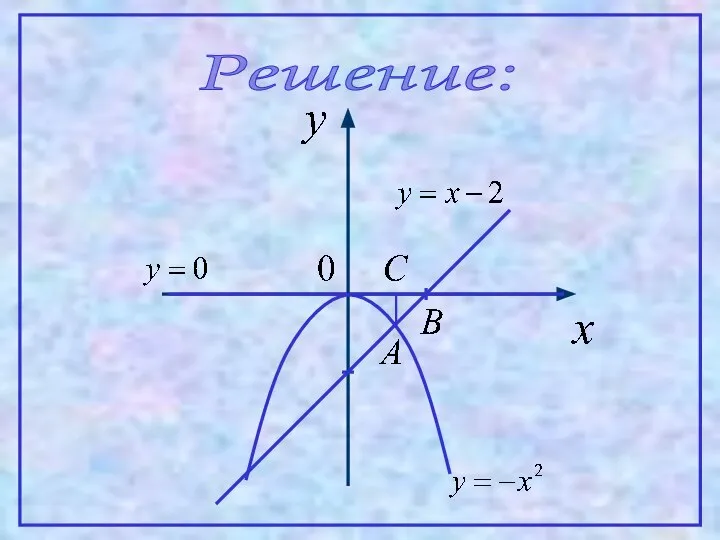
- 6. Пример. Вычислить площадь фигуры, ограниченной линиями:
- 7. Решение:
- 8. SОАВ – это площадь над кривой ОАВ на отрезке [0;2]. Но эта кривая задается не одним
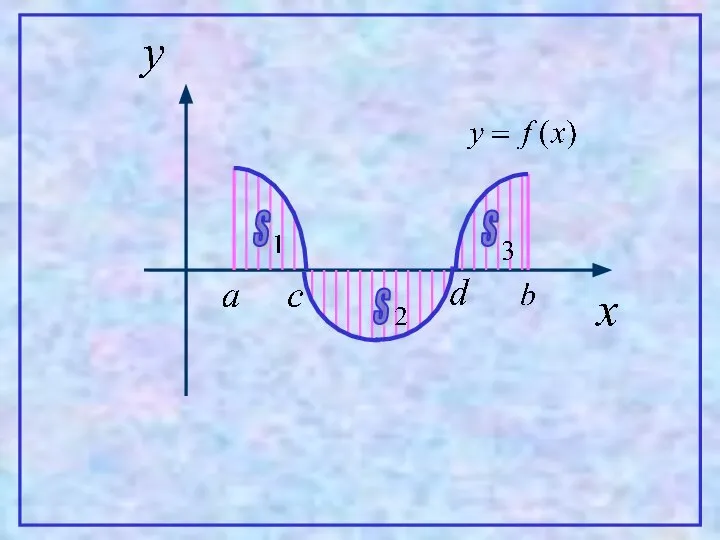
- 9. 3 Пусть функция y=f(x) – непрерывна на [a,b] и исходный отрезок можно разбить на определенное число
- 10. S S S
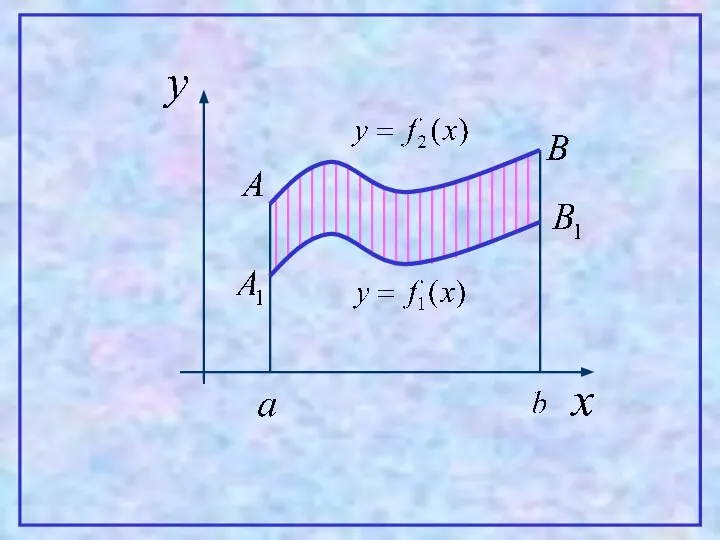
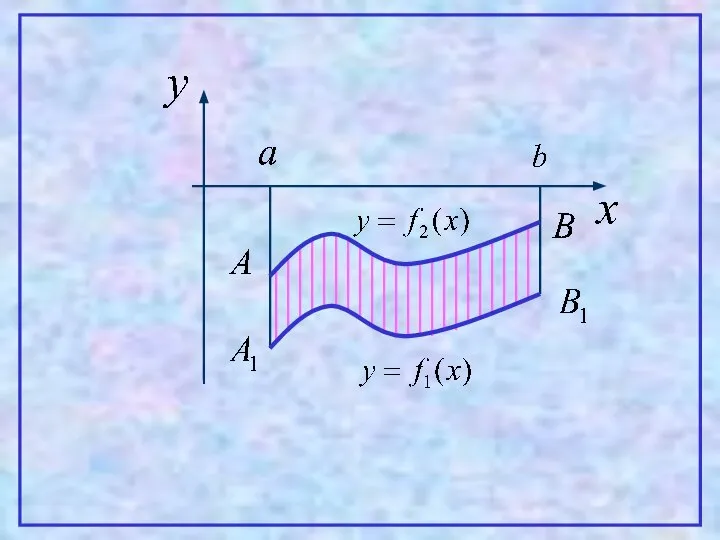
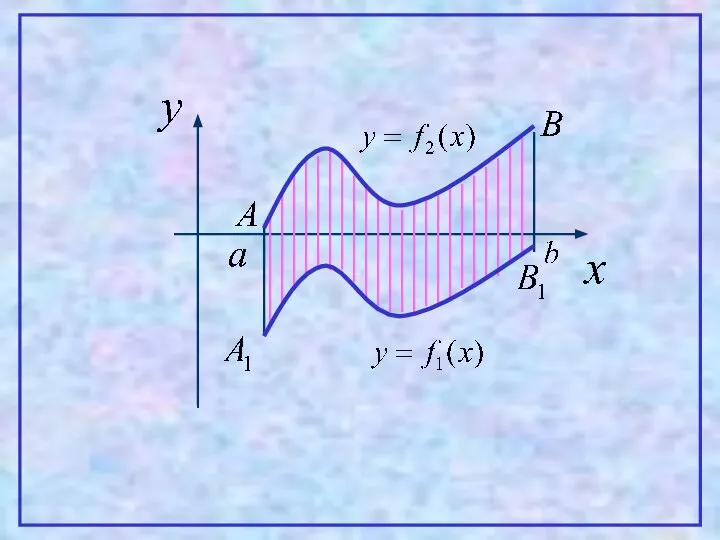
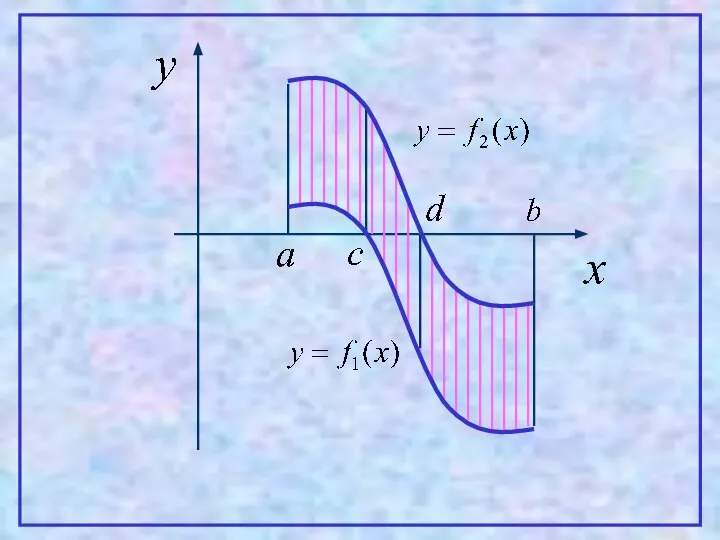
- 12. 4 Теорема. Пусть на [a,b] заданы непрерывные функции y=f1(x) и y=f2(x), такие что Тогда площадь фигуры,
- 13. Проиллюстрируем эту теорему графически. Рассмотрим несколько случаев. 1
- 16. 2
- 19. 3
- 22. 4 Общий случай. Этот случай сводится к рассмотренным случаям 1-3, если разбить отрезок [a,b] на элементарные
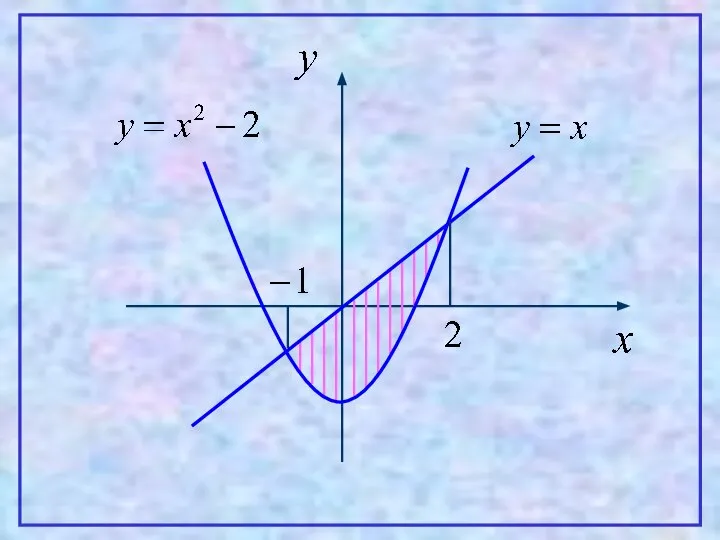
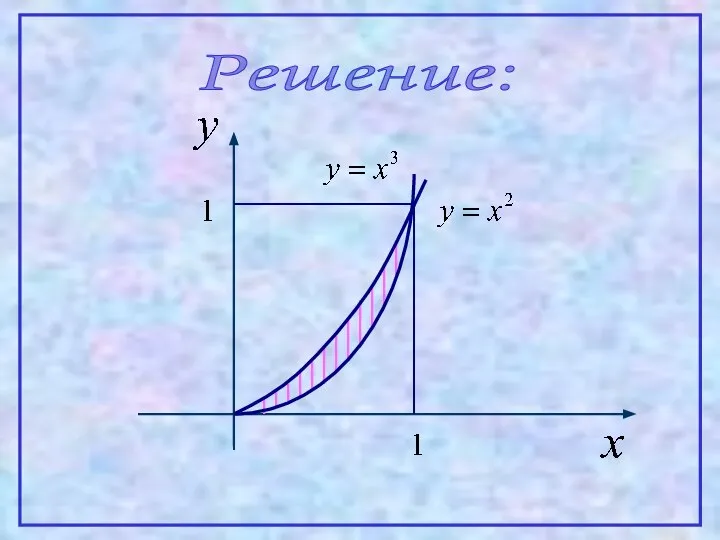
- 24. Пример. Вычислить площадь фигуры, ограниченной линиями:
- 26. Решение: Находим координаты точек пересечения линий: Следовательно, линии пересекаются в точках
- 27. 2. Вычисление объемов тел вращения Пусть функция y=f(x) –знакопостоянная и непрерывна на [a,b]. Найти объем тела
- 29. Тогда некоторое приближение для искомого объема даст сумма Так как каждое слагаемое это объем цилиндра с
- 30. Правая часть выражения представляет собой предел интегральной суммы функции Поэтому
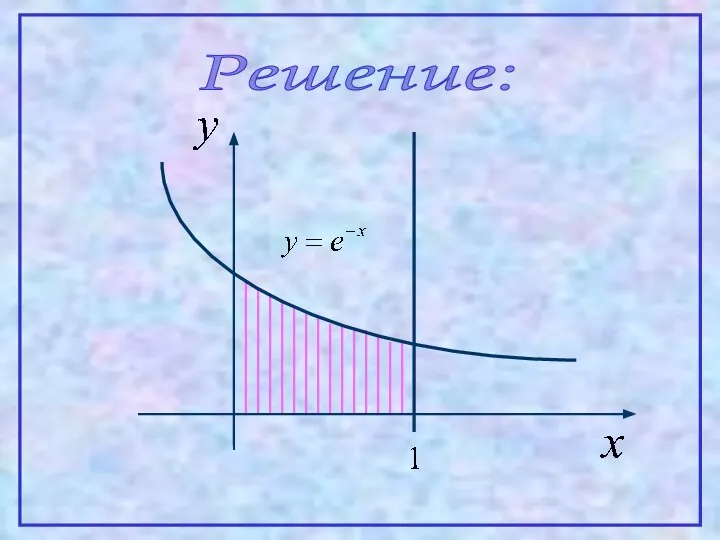
- 31. Пример. Вычислить объем тела, полученного от вращения вокруг оси абсцисс фигуры, ограниченной линиями:
- 32. Решение:
- 34. Если заменить х на у, то получим формулу для вычисления объема тела, полученного от вращения криволинейной
- 35. Пример. Вычислить объем тела, полученного от вращения вокруг оси ординат фигуры, ограниченной линиями:
- 36. Решение:
- 38. Скачать презентацию


![2 Пусть функция y=f(x) – неположительная и непрерывна на [a,b]. Отражая кривую](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1140657/slide-4.jpg)

![SОАВ – это площадь над кривой ОАВ на отрезке [0;2]. Но эта](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1140657/slide-7.jpg)
![3 Пусть функция y=f(x) – непрерывна на [a,b] и исходный отрезок можно](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1140657/slide-8.jpg)
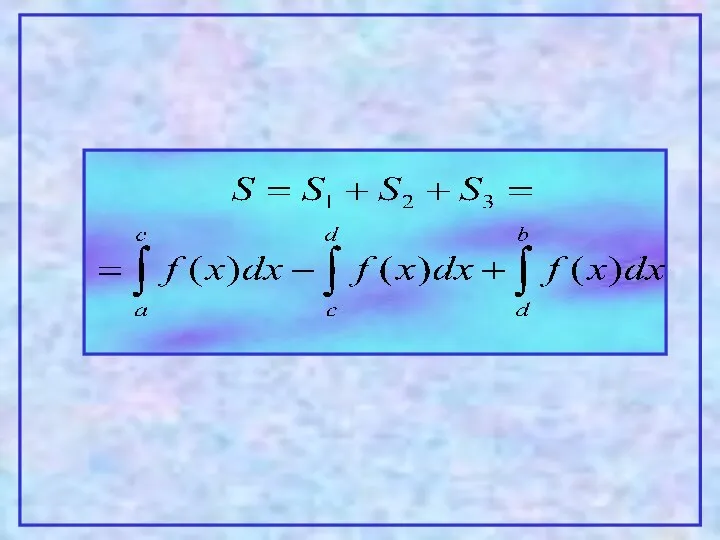
![4 Теорема. Пусть на [a,b] заданы непрерывные функции y=f1(x) и y=f2(x), такие](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1140657/slide-11.jpg)

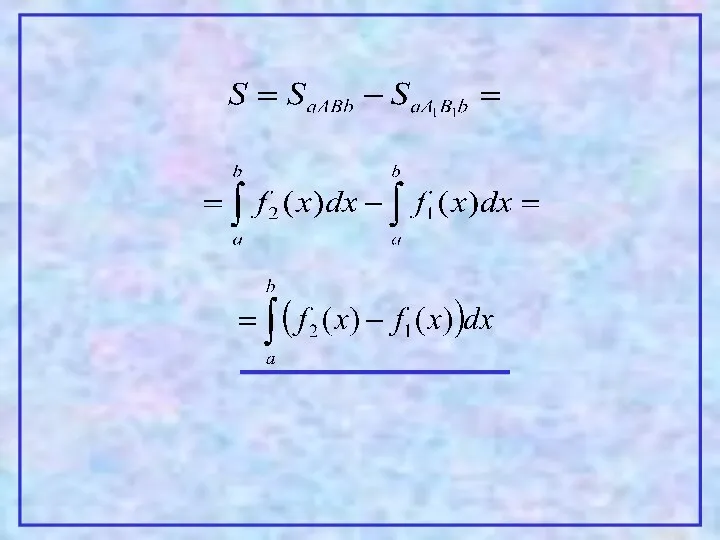

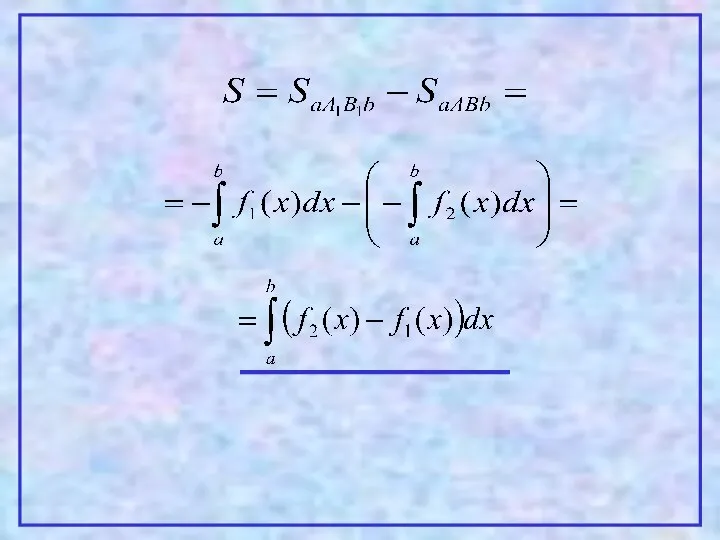

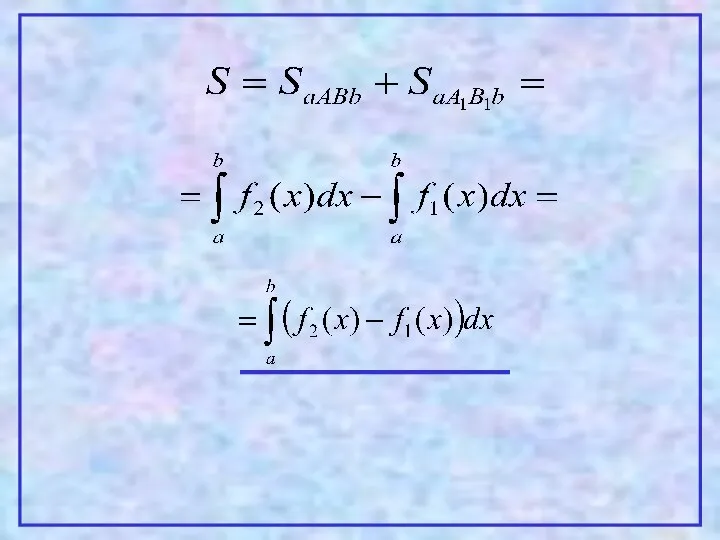




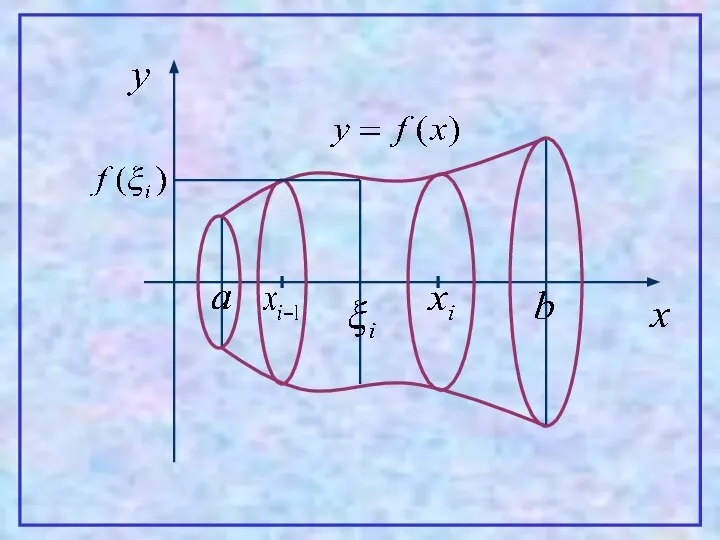



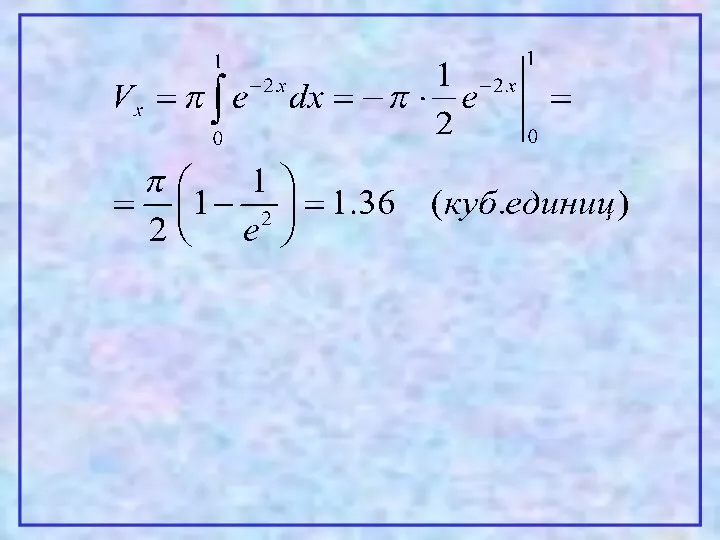


 Приёмы устных вычислений вида 260+310, 670-140
Приёмы устных вычислений вида 260+310, 670-140 Презентация на тему Свойства сложения и умножения
Презентация на тему Свойства сложения и умножения  Производная функции
Производная функции Свертка функций Формулы обращения Теоремы разложения
Свертка функций Формулы обращения Теоремы разложения Uravnenia_i_neravenstva_Sistemy_uravneniy
Uravnenia_i_neravenstva_Sistemy_uravneniy Виды векторов
Виды векторов Функция y=k/x, её график и свойства. 8 класс. Урок 3
Функция y=k/x, её график и свойства. 8 класс. Урок 3 Метод сложения
Метод сложения Презентация на тему Старинные русские меры
Презентация на тему Старинные русские меры  Азбука
Азбука На лесной поляне
На лесной поляне Уголок математики в подготовительной группе
Уголок математики в подготовительной группе Математика
Математика Признаки равенства треугольников. Подготовка к контрольной работе
Признаки равенства треугольников. Подготовка к контрольной работе Векторы на плоскости и в пространстве
Векторы на плоскости и в пространстве Уроки геометрии в 8 классе
Уроки геометрии в 8 классе Алгоритм решения комбинаторных задач
Алгоритм решения комбинаторных задач Квадратичная функция
Квадратичная функция Прикладная статистика. Доверительные интервалы для среднего. Критерий t Стьюдента. Критерии Уилкоксона для ранговых сравнений
Прикладная статистика. Доверительные интервалы для среднего. Критерий t Стьюдента. Критерии Уилкоксона для ранговых сравнений Первообразная
Первообразная Обыкновенные и десятичные дроби. Вводное повторение. 7 класс
Обыкновенные и десятичные дроби. Вводное повторение. 7 класс Геометриялық фигуралар
Геометриялық фигуралар Презентация на тему ГРАФИК ДВИЖЕНИЯ
Презентация на тему ГРАФИК ДВИЖЕНИЯ  Логарифмические неравенства
Логарифмические неравенства Десятки и единицы
Десятки и единицы Линейные пространства и линейные операторы. Лекция 3
Линейные пространства и линейные операторы. Лекция 3 Призма
Призма Математическая статистика результатов ЕГЭ
Математическая статистика результатов ЕГЭ