Особенности математических моделей, влияющих на выбор методов

Математическая функциональная модель в общем случае представляет собой алгоритм вычисления вектора выходных параметров Y при заданных векторах параметров элементов X и внешних параметров Q. Математические модели могут быть символическими и численными.При использовании символических моделей оперируют не значениями величин, а их символическими обозначениями(идентификаторами).Численные модели могут быть аналитическими, т.е. их можно представить в виде явно выраженных зависимостей выходных параметров Y от параметров внутренних X и внешних Q, или алгоритмическими, в которых связь Y , X и Q задана неявно в виде алгоритма моделирования. Важнейший частный случай алгоритмических моделей-имитационные, они отображают процессы в системе при наличии внешних воздействий на систему. Другими словами, имитационная модель-это алгоритмическая поведенческая модель. Классификацию математических моделей выполняют также по ряду других признаков. Так, в зависимости от принадлежности к тому или иному иерархическому уровню выделяют модели уровней системного, функционально логического, макроуровня (сосредоточенного) и микроуровня (распределенного).

По характеру используемого для описания математического аппарата различают модели лингвистические, теоретико-множественные, абстрактно-алгебраические, нечеткие, автоматные и т.п.
Например,на системном уровне преимущественно применяют модели систем массового обслуживания и сети Петри,на функционально-логическом уровне
-автоматные модели на основе аппарата передаточных функций или конечных автоматов, на макроуровне-системы алгебраических и дифференциальных уравнений, на микроуровне-дифференциальные уравнения в частных производных. Особое место занимают геометрические модели, используемые в системах конструирования.

Кроме того, введены понятия полных моделей и макромоделей, моделей
статических и динамических, детерминированных и стохастических, аналоговых
и дискретных, символических и численных.
Полная модель объекта в отличие от макромодели описывает не только
процессы на внешних выводах моделируемого объекта, но и внутренние для
объекта процессы.
Статические модели описывают статические состояния, в них не присутствует время в качестве независимой переменной. Динамические модели отражают поведение системы, т.е.в них обязательно используется время.
Стохастические и детерминированные модели различают в зависимости от
учета или не учета случайных факторов.
В аналоговых моделях фазовые переменные-непрерывные величины, в
дискретных-дискретные, в частном случае дискретные модели являются
логическими(булевыми),в них состояние системы и ее элементов описывается
булевыми величинами. В ряде случаев полезно применение смешанных моделей, в которых одна часть подсистем характеризуется аналоговыми моделями, другая-логическими.

Методы и алгоритмы анализа на макроуровне
Анализ процессов в проектируемых объектах можно проводить во временной и частотной областях. Анализ во временной области (динамический анализ) позволяет получить картину переходных процессов, оценить динамические свойства объекта, он является важной процедурой при исследовании как линейных, так и нелинейных систем. Анализ в частотной области более специфичен, его применяют, как правило, к объектам с линеаризуемым и математическим и моделями при исследовании колебательных стационарных процессов, анализе устойчивости, расчете искажений информации,представляемой
спектральными составляющими сигналов,ит.п.

Методы анализа во временной области, используемые в универсальных программах анализа в САПР,—это численные методы интегрирования систем обыкновенных дифференциальных уравнений (СОДУ):
Другими словами, это методы алгебраизации дифференциальных уравнений. Формулы интегрирования СОДУ могут входить в математическую модель независимо от компонентных уравнений, или
быть интегрированным и в математические модели компонентов.

От выбора метода решения СОДУ существенно зависят такие характеристики анализа, как точность и вычислительная эффективность. Эти характеристики определяются прежде всего типом и порядком выбранного метода интегрирования СОДУ.
Применяют два типа методов интегрирования—явные (иначе экстраполяционные, или методы, основанные на формулах интегрирования вперед) инеявные (интерполяционные, основанные на формулах интегрирования назад).Различия между ними удобно показать на примере простейших методов первого порядка—методов Эйлера.
Формула явного метода Эйлера представляет собой следующую формулу
замены производных в точке tn :

Методы решения систем нелинейных
алгебраических уравнений
Вычисления при решении СОДУ состоят из нескольких вложенных один в другой циклических процессов. Внешний цикл—это цикл пошагового численного
интегрирования, параметром цикла является номер шага. Если модель анализируемого объекта нелинейна, то на каждом шаге выполняется промежуточный цикл—итерационный цикл решения системы нелинейных алгебраических
уравнений(СНАУ).Параметр цикла—номер итерации. Во внутреннем цикле решается СЛАУ. Для решения СНАУ можно применять прямые итерационные методы, та-кие, как метод простой итерации или метод Зейделя, но в современных программах анализа наибольшее распространение получил метод Ньютона, основанный налинеаризации СНАУ.

Методы решения систем линейных
алгебраических уравнений

Методы анализа на микроуровне
В САПР решение дифференциальных или интегро- дифференциальных уравнений с частными производными выполняется численными методами. Эти методы основаны на дискретизации независимых переменных—их представлении конечным множеством значений в выбранных узловых точках
исследуемого пространства . Эти точки рассматриваются как узлы некоторой сетки, поэтому используемые в САПР методы—это сеточные методы.
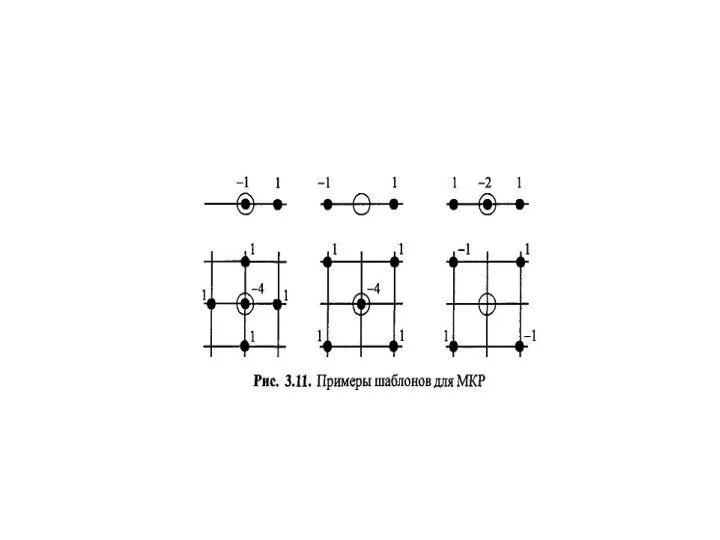
Среди сеточных методов наибольшее распространение получили два метода: метод конечных разностей(МКР ) и МКЭ . Обычно выполняют дискретизацию пространственных независимых переменных, т.е. Используют пространственную сетку. В этом случае результатом дискретизации является СОДУ
для задачи нестационарной или система алгебраических уравнении для стационарной. Пусть необходимо решить уравнение