Математика.Управление социальными системами. Математический анализ. Функции. Пределы. Непрерывность

Последовательности

Предел последовательности

Предел последовательности

Предел последовательности

Число e
Можно доказать, что последовательность является
возрастающей и ограниченной и, следовательно, имеет предел.
Определение. Числом e или числом Эйлера называется предел
последовательности :
Число e – иррациональное и трансцендентное, т.е. оно не является корнем многочлена с целочисленными коэффициентами.

Функции

Основные элементарные функции

Предел функции в точке

Предел функции в точке

Предел функции в точке
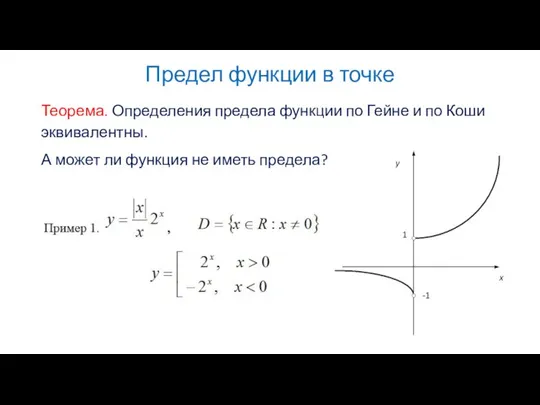
Теорема. Определения предела функции по Гейне и по Коши эквивалентны.
А может ли функция не иметь предела?

Односторонние пределы
Обозначение:

Односторонние пределы

Предел в бесконечно удаленной точке
Обозначение:

Предел в бесконечно удаленной точке
Пример 2.

СВОЙСТВА ПРЕДЕЛОВ

ПРИЕМЫ ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ

ПРИЕМЫ ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ

ПРИЕМЫ ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
Вычисление предела сводится к «раскрытию неопределенности», т.е. к выполнению некоторых тождественных преобразований, позволяющих избавиться от неопределенности.

ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ
Первый замечательный предел:
Следствие.

ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ
Второй замечательный предел.
Теорема. Существует предел функции при равный числу e.
Заменой получим
Следствие.

Бесконечно малые функции

Использование бесконечно малых для вычисления пределов
При вычислении пределов удобно использовать эквивалентность следующих бесконечно малых функций при x→0:

Использование бесконечно малых для вычисления пределов
Пример 6.

НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Теорема. Элементарная функция непрерывна на каждом интервале, целиком содержащемся в области её определения.

НЕПРЕРЫВНОСТЬ ФУНКЦИИ

ТОЧКИ РАЗРЫВА ФУНКЦИИ

Точка устранимого разрыва

Точка разрыва1 рода

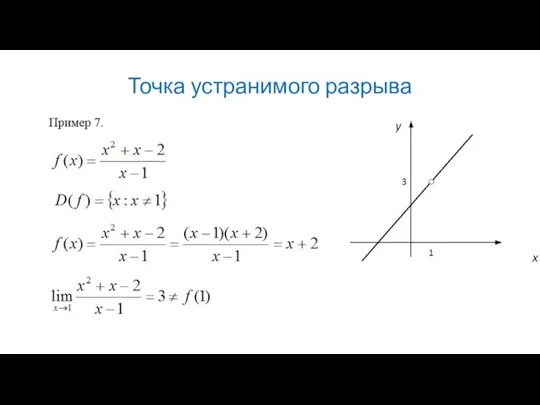
Точка разрыва1 рода
Пример 1 (продолжение).

Точка разрыва1 рода
Пример 8