Материалы к урокам и факультативным занятиям для 11 класса

Материалы к урокам и факультативным занятиям
для 11класса
Учитель ГБОУ гимназии № 49 Приморского района Санкт-Петербурга
Алексеевой Людмилы Васильевны

«Если имеются две неравные площади,
то, постоянно прибавляя к самому себе
избыток, на который большая площадь
превосходит меньшую, можно получить
площадь, которая была бы больше
любой заданной ограниченной площади.»
Архимед

Криволинейной трапецией называют фигуру, ограниченную графиком непрерывной функции, заданной на отрезке [a;b] и принимающей на нем положительные значения, отрезками прямых х=а и х=b и отрезком [a;b] оси абсцисс.
Определение.

Найти площадь криволинейной трапеции можно
способом последовательных приближений
способом составления интегральных сумм
используя определенный интеграл

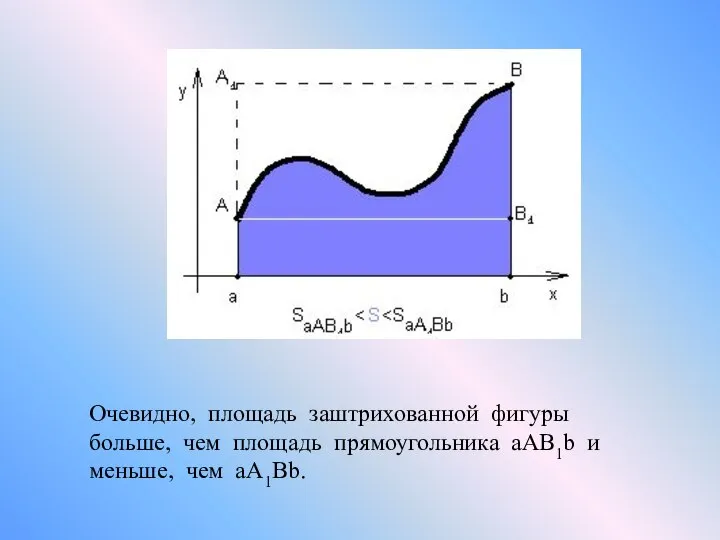
Очевидно, площадь заштрихованной фигуры больше, чем площадь прямоугольника aАB1b и меньше, чем aA1Bb.

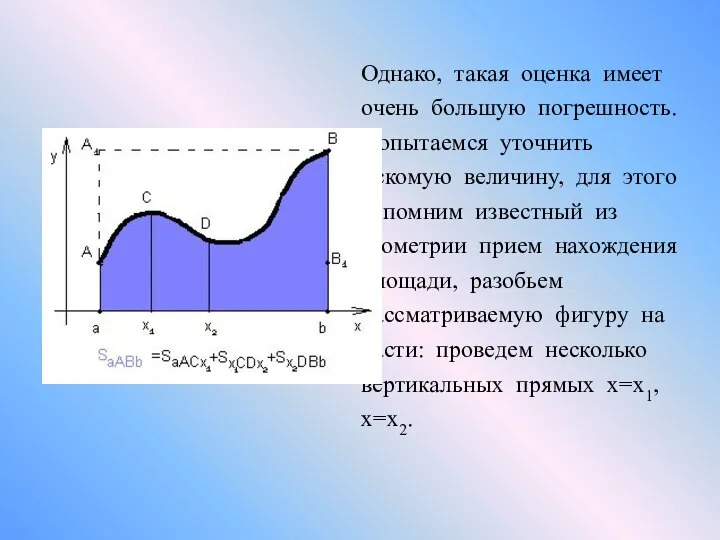
Однако, такая оценка имеет очень большую погрешность. Попытаемся уточнить искомую величину, для этого вспомним известный из геометрии прием нахождения площади, разобьем рассматриваемую фигуру на части: проведем несколько вертикальных прямых х=х1, х=х2.

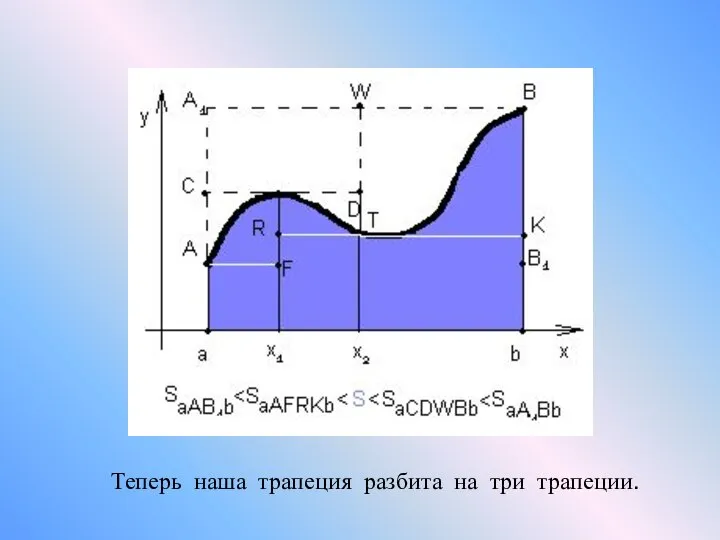
Теперь наша трапеция разбита на три трапеции.

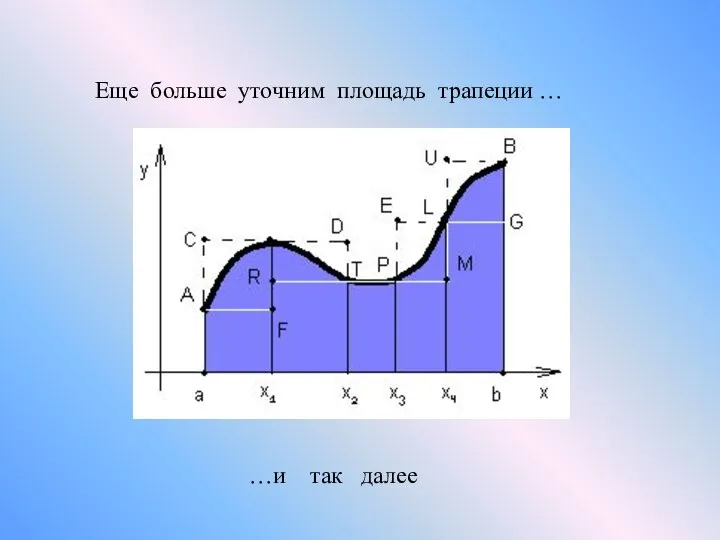
Еще больше уточним площадь трапеции …
…и так далее

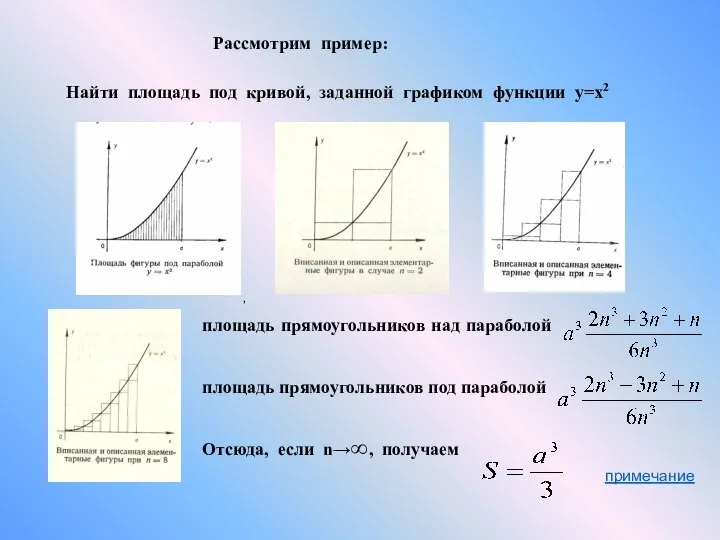
Рассмотрим пример:
Найти площадь под кривой, заданной графиком функции у=х2
площадь прямоугольников над параболой
,
площадь прямоугольников под параболой
Отсюда, если n→∞, получаем
примечание

Нахождение суммы последовательности
квадратов натуральных чисел
справедлива формула
доказательство можно провести по индукции

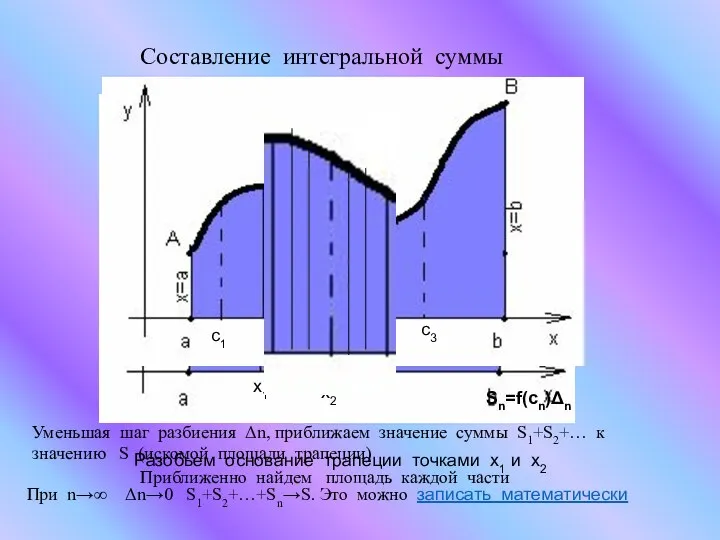
Составление интегральной суммы
Разобьем основание трапеции точками x1 и х2
Приближенно найдем площадь каждой части
Sn=f(cn)Δn
Уменьшая шаг разбиения Δn, приближаем значение суммы S1+S2+… к значению S (искомой площади трапеции)
При n→∞ Δn→0 S1+S2+…+Sn→S. Это можно записать математически

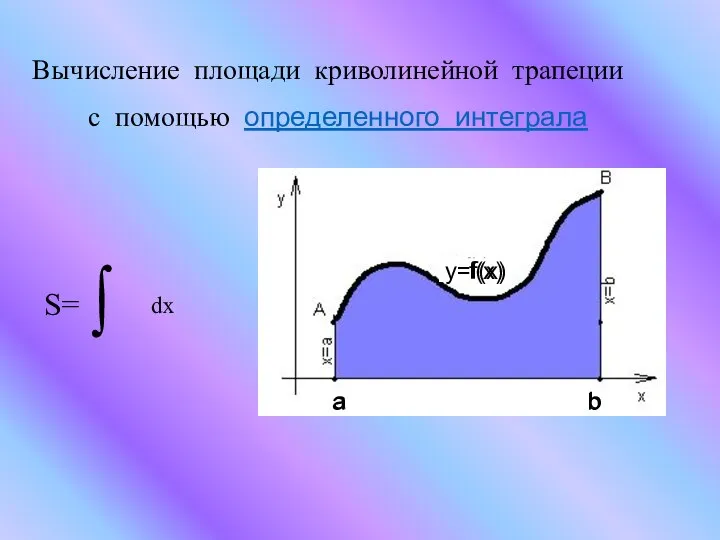
Вычисление площади криволинейной трапеции
с помощью определенного интеграла
S=
∫
dx
a
b
f(x)
y=f(x)
a
b

Вычисление определенного интеграла.
Формула Ньютона – Лейбница

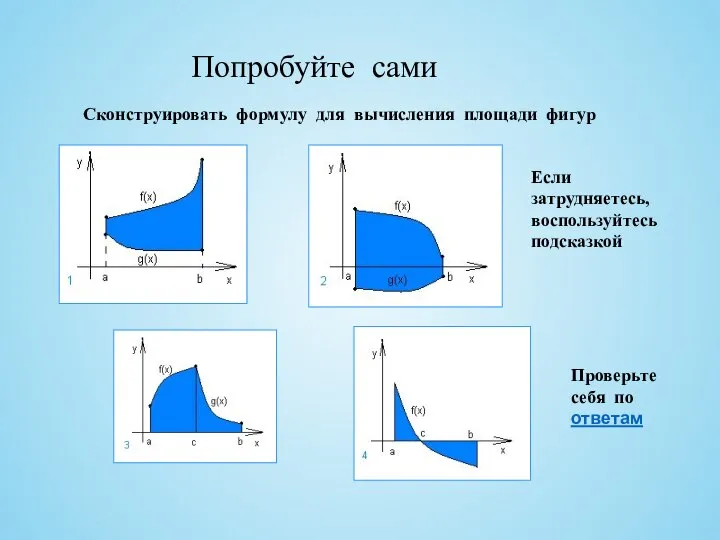
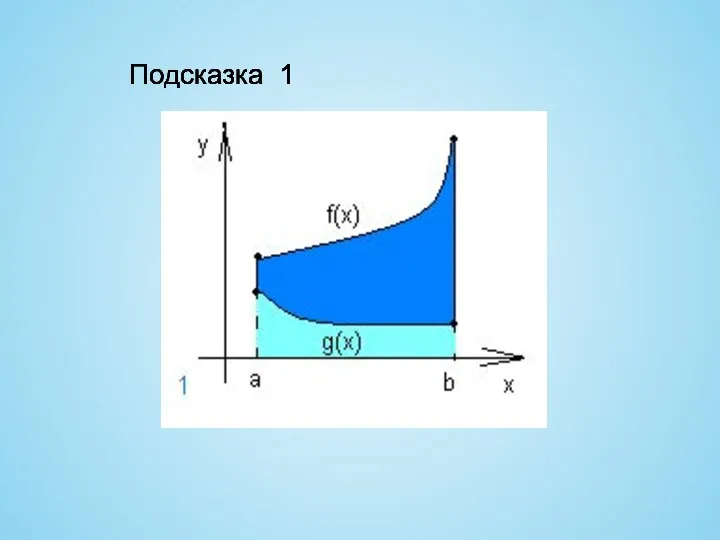
Попробуйте сами
Сконструировать формулу для вычисления площади фигур
Если затрудняетесь, воспользуйтесь подсказкой
Проверьте себя по ответам

Подсказка 1
Подсказка 1
Подсказка 1
Подсказка 1

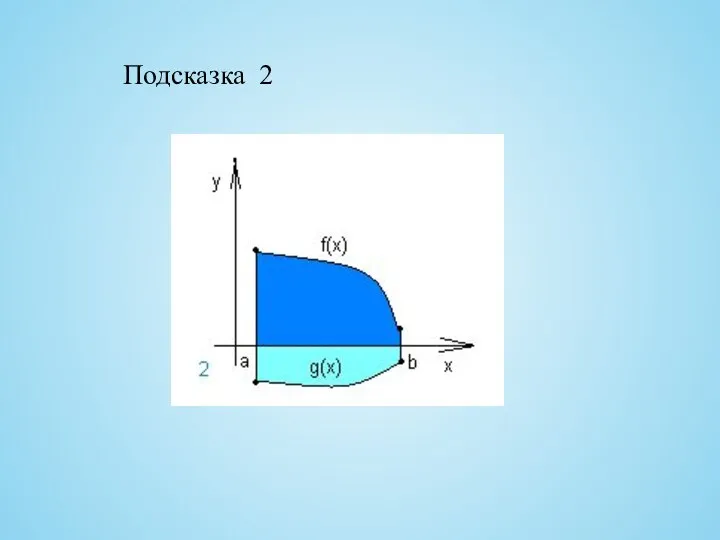
Подсказка 2

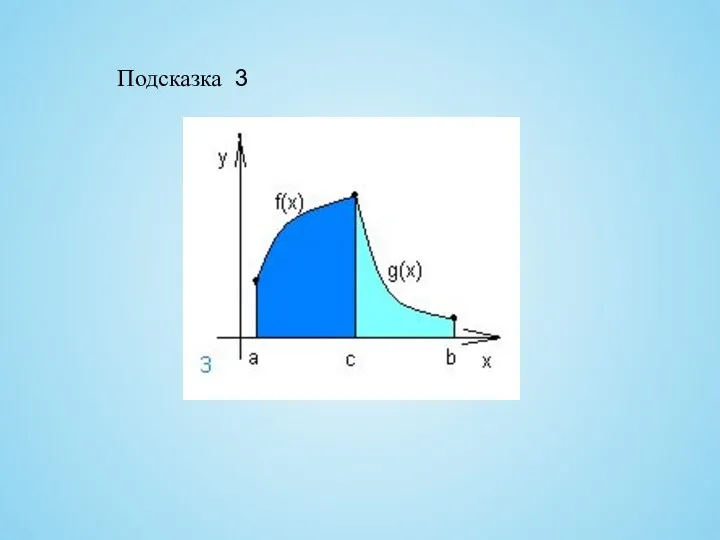
Подсказка 3

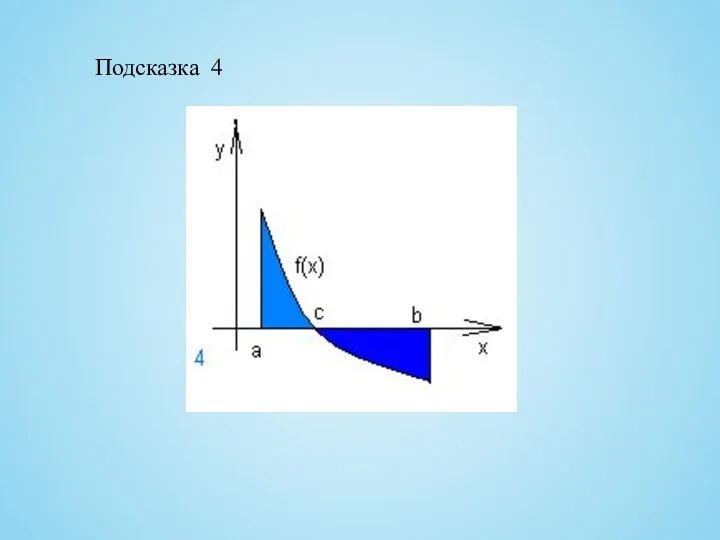
Подсказка 4