Содержание
- 2. Старинная задача о кроликах и фазанах Некто подошел к клетке, в которой сидели фазаны и кролики.
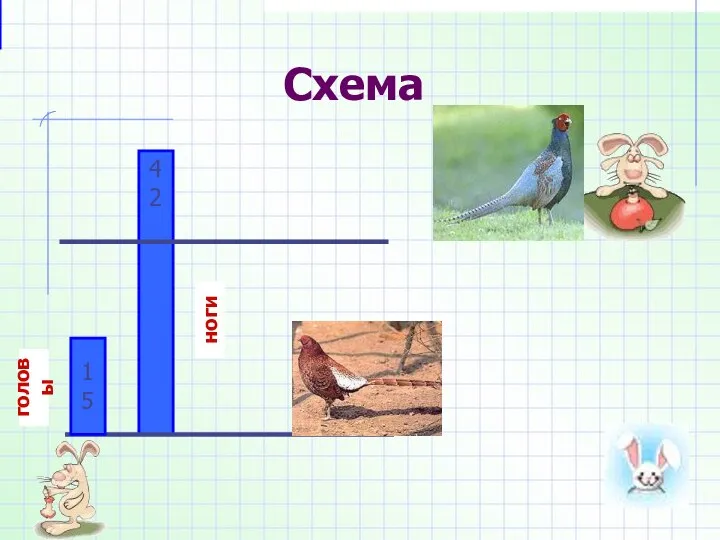
- 3. Схема 15 42 15 12 головы ноги
- 4. Решение задачи 2=30 (лап) 42-30=12 (лап лишних) – лапы кроликов 12:2=6 (кроликов) 15-6 = 9 (фазанов)
- 5. Решение задачи с помощью уравнения Кролики Фазаны кол-во лапы 4х+2(15-х)=42 4х+30-2х=42 4х-2х=42-30 2х=12 Х=12:2 Х=6 Если
- 6. Страницы истории По-гречески «число» - арифмос. Почти все науки зародились в Греции, один из разделов математики
- 7. Страницы истории Абу Абдалах Мухаммед ибн Муса ал-Хорезми – выдающийся средневековый ученый, внесший большой вклад в
- 8. Аль-Хорезми первым написал книгу на арабском языке о решении уравнений Книга называлась «Китаб мухтасар аль джебр
- 9. algebr
- 10. Ал-джабра При решении уравнения Если в части одной, Безразлично какой, Встретится член отрицательный, Мы к обеим
- 11. Ал-мукабала Дальше смотрим в уравнение, Можно ль сделать приведенье, Если члены в нем подобны, Сопоставить их
- 12. 6х -13 2х -5 = 13 -2х 4х = 8 2 = х Ал-джабра Ал-мукабала Решить
- 13. Отец алгебры Франсуа Виет Сам он слово «алгебра» не применял. И называл он её «аналитическим искусством»,
- 14. В процессе развития алгебра из науки об уравнениях преобразовалась в науку об операциях, более или менее
- 15. В основе алгебраического языка лежит непривычный «алфавит» 1. Числа 2. Буквы латинского алфавита В зависимости от
- 16. «Люди, незнакомые с алгеброй, не могут представить себе тех удивительных вещей, которых можно достигнуть … при
- 18. Скачать презентацию














 Прямоугольный параллелепипед
Прямоугольный параллелепипед Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений Множества и отображения
Множества и отображения Последовательности
Последовательности Презентация на тему Загадочное число Пи
Презентация на тему Загадочное число Пи  Презентация на тему Прямоугольные треугольники
Презентация на тему Прямоугольные треугольники 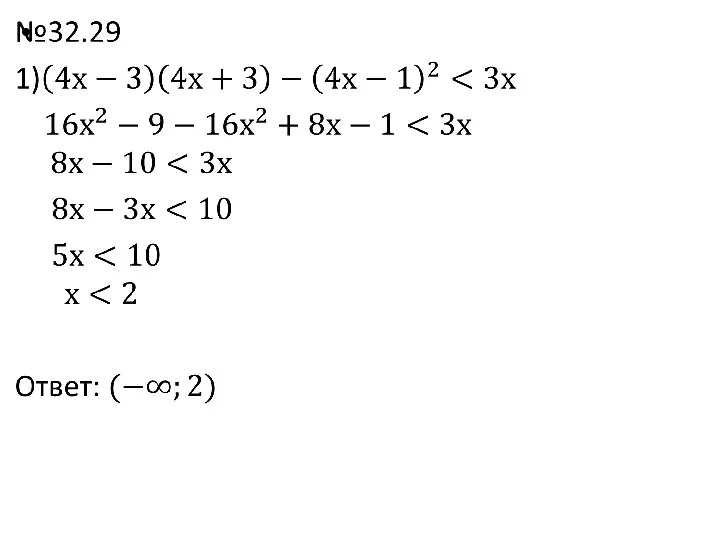 Формулы куба суммы и куба разности двух выражений
Формулы куба суммы и куба разности двух выражений Расчёт радиатора для транзистора
Расчёт радиатора для транзистора Простейшие функции. Операция суперпозиции
Простейшие функции. Операция суперпозиции Решение задач по теме: Параллелограмм (1)
Решение задач по теме: Параллелограмм (1) Азбука
Азбука Решение линейных уравнений с одной переменной
Решение линейных уравнений с одной переменной Занимательная геометрия
Занимательная геометрия Метод решения систем линейных уравнений методом Крамера
Метод решения систем линейных уравнений методом Крамера Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной
Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной Решение уравнений и построение точек по их координатам. 6 класс
Решение уравнений и построение точек по их координатам. 6 класс Решение задач на нахождение значений двух величин по сумме и разности
Решение задач на нахождение значений двух величин по сумме и разности Презентация на тему Формулы приведения
Презентация на тему Формулы приведения  Параллель к перпендикуляру
Параллель к перпендикуляру Презентация
Презентация Алгоритмы на графах
Алгоритмы на графах Путь и перемещение
Путь и перемещение Глубина озера. Теорема Пифагора
Глубина озера. Теорема Пифагора Интервальное оценивание параметров распределения
Интервальное оценивание параметров распределения Тригонометрия в жизни
Тригонометрия в жизни Сравнительный анализ лирики А.С. Пушкина и В.В. Маяковского методами математической статистики
Сравнительный анализ лирики А.С. Пушкина и В.В. Маяковского методами математической статистики Вычислительная математика. Вычисление серии интегралов. Вычисление корней квадратного уравнения. Вычисление exp(x)
Вычислительная математика. Вычисление серии интегралов. Вычисление корней квадратного уравнения. Вычисление exp(x) Сфера и плоскость
Сфера и плоскость