Содержание
- 2. Мы рассмотрим задачи, в которых нужно узнать изменения объёма или площади поверхности при увеличении (уменьшении) линейных
- 3. Учитываем и запоминаем: Объёмное тело рассматриваем в трёхмерном пространстве. Значит все изменения с ним происходят по
- 4. Теорема. Пусть дан объем исходного многогранника Vстарый. Пусть также известны числа a, b и c —
- 5. В задаче: «Длина основания уменьшена в 2 раза, ширина увеличена в 5 раз, а высота увеличена
- 6. Задача. Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 8 раз, а
- 7. Обратите внимание: Растяжение произошло сразу по двум осям. Окружность — фигура двумерная. Поэтому изменение радиуса у
- 8. № 1. Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше,
- 9. № 1. Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше,
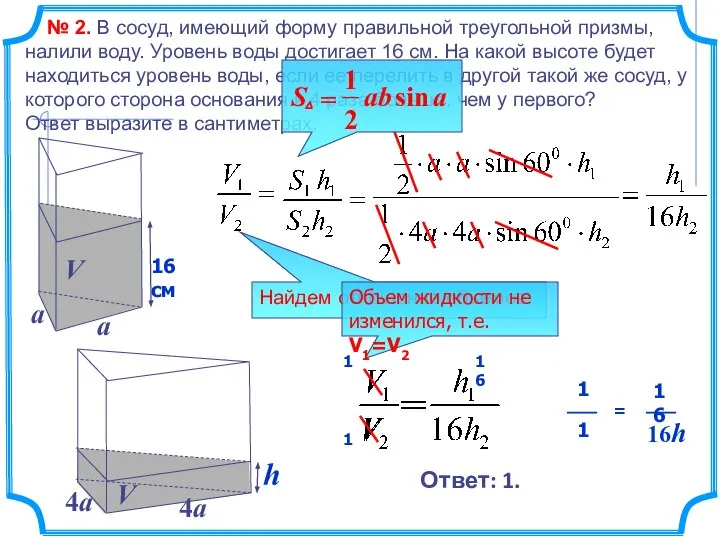
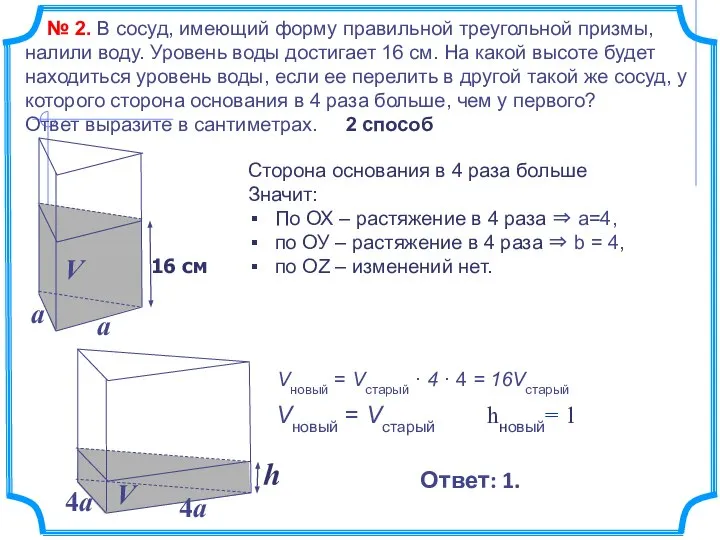
- 10. № 2. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см.
- 11. № 2. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см.
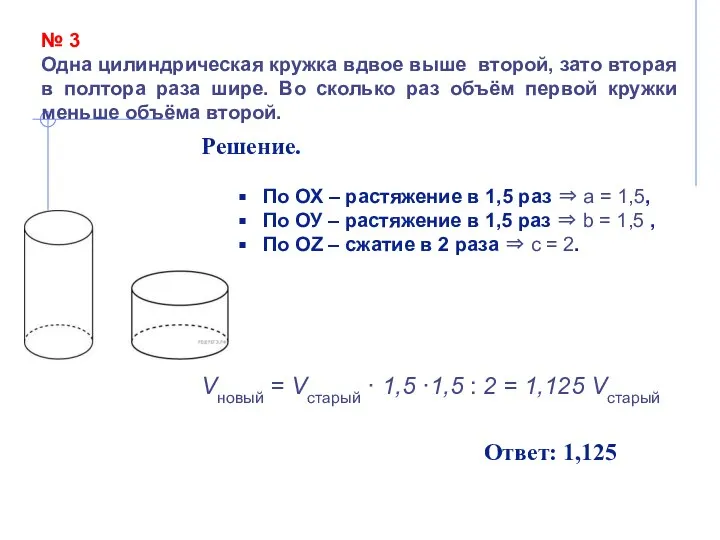
- 12. № 3 Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Во сколько
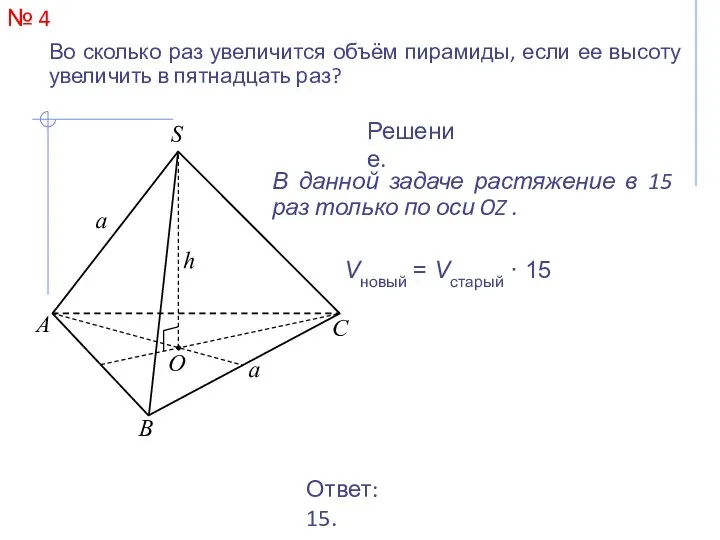
- 13. № 4 Во сколько раз увеличится объём пирамиды, если ее высоту увеличить в пятнадцать раз? Ответ:
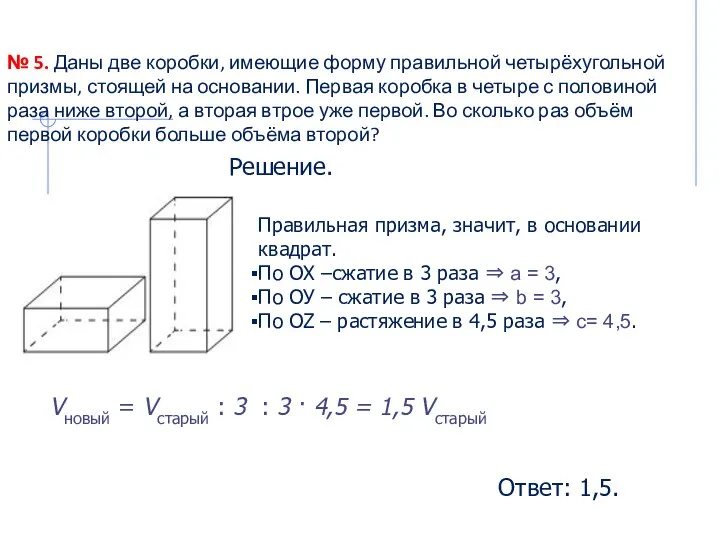
- 14. № 5. Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в
- 15. № 6. Бетонный шар весит 0,75 т. Сколько будет весить шар, изготовленный из того же материала,
- 16. Теорема. Формула площадей очень похожа на частный случай формулы объемов. Разница лишь в степени: Vновый =
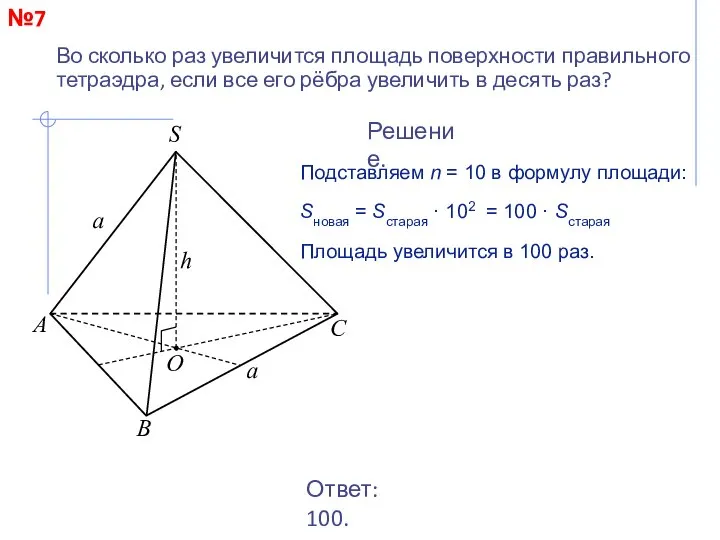
- 17. №7 Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его рёбра увеличить в десять
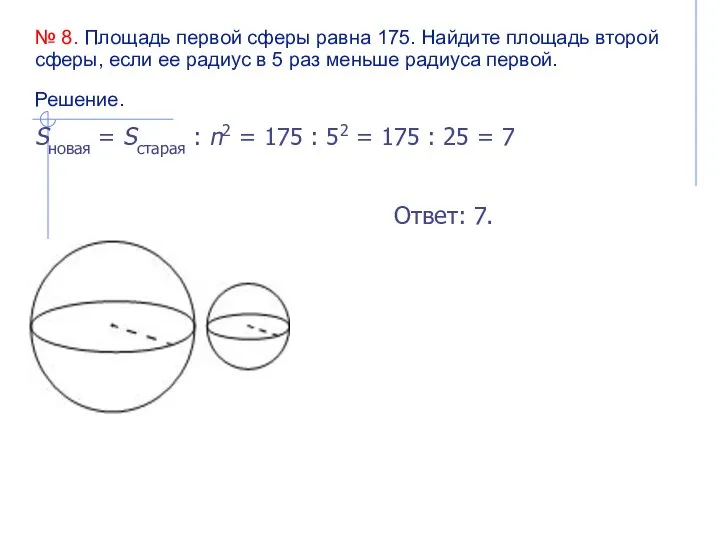
- 18. № 8. Площадь первой сферы равна 175. Найдите площадь второй сферы, если ее радиус в 5
- 19. № 9. В пространстве даны два прямых круговых конуса. У второго конуса радиус основания и высота
- 21. Скачать презентацию











 Проверка деления умножением
Проверка деления умножением izmerenie_otrezkov_7_klass
izmerenie_otrezkov_7_klass Телдән исәпләү
Телдән исәпләү Теорема Байеса
Теорема Байеса Zaokrugljivanje decimalnih brojeva
Zaokrugljivanje decimalnih brojeva Степень с натуральным показателем. Занимательные задания
Степень с натуральным показателем. Занимательные задания соответствия
соответствия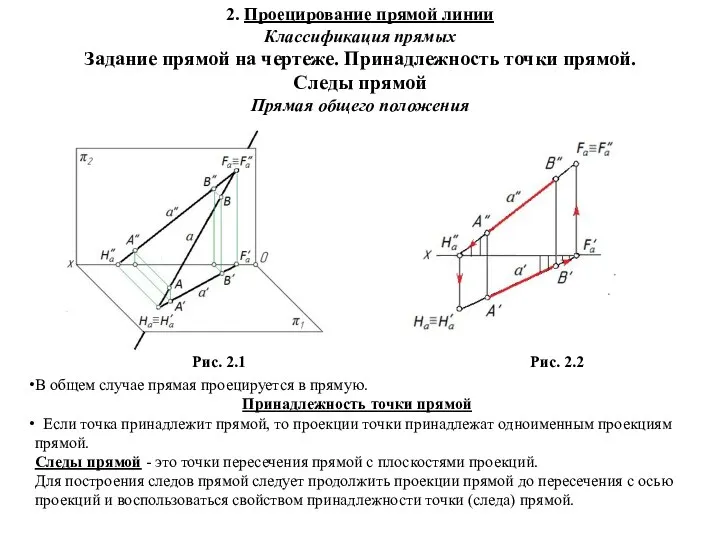 Начертательная геометрия. Проецирование прямой линии
Начертательная геометрия. Проецирование прямой линии Логарифмическая функция
Логарифмическая функция Презентация на тему Игра по математике "Счастливый случай"
Презентация на тему Игра по математике "Счастливый случай"  Дифференциал функции
Дифференциал функции Презентация на тему Тесты по математике
Презентация на тему Тесты по математике  Тест по математике
Тест по математике Презентация на тему Решение неравенств методом интервалов
Презентация на тему Решение неравенств методом интервалов  Теорема косинусов
Теорема косинусов Занимательная геометрия
Занимательная геометрия Правильные многоугольники в природе. Геометрия пчелиных сот
Правильные многоугольники в природе. Геометрия пчелиных сот Прибавить и вычесть 3. Решение текстовых задач. Урок №57
Прибавить и вычесть 3. Решение текстовых задач. Урок №57 Координатные векторы
Координатные векторы Решение задач Параллельные прямые
Решение задач Параллельные прямые Измерение объема жидких и сыпучих веществ с помощью условной меры масс
Измерение объема жидких и сыпучих веществ с помощью условной меры масс Сумма углов треугольника
Сумма углов треугольника Линейная зависимость и линейная независимость системы векторов. Семинар 4
Линейная зависимость и линейная независимость системы векторов. Семинар 4 Арифметичская прогрессия
Арифметичская прогрессия Орел. Решка. Формула вероятности
Орел. Решка. Формула вероятности Квадратные уравнения
Квадратные уравнения Решение задач. Таблица умножения на 6. Кратное сравнение чисел
Решение задач. Таблица умножения на 6. Кратное сравнение чисел Условный оператор задач
Условный оператор задач