Содержание
- 2. У гражданина Лукина 1 августа 2000 года родился сын. По этому случаю он открыл в некотором
- 3. Через n лет величина вклада в первом банке будет: Через n лет после открытия первого вклада
- 4. Через сколько лет после рождения сына суммы на каждом из двух вкладов сравняются, если деньги из
- 5. 31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10%
- 6. Пусть ежегодная выплата равна х, обозначим сумму кредита -a,
- 7. Ответ: 3993000.
- 8. В банк помещена сумма 3900 тысяч рублей под 50% годовых. В конце каждого из первых четырех
- 9. В банк помещена сумма 3900 тысяч рублей под 50% годовых. Через год внесена первая добавка (х),
- 10. Через пять лет забрал деньги (из последнего столбика).
- 11. К концу пятого года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным
- 12. Ответ: 210 тыс.рублей. 210 тыс. рублей вкладчик ежегодно добавлял к вкладу
- 13. В начале года 5/6 некоторой суммы денег вложили в банк А, а остальное – в банк
- 17. Ответ:841.
- 18. Фермер получил кредит в банке под определенный процент годовых. Через год фермер в счет погашения кредита
- 19. Фермер получил кредит А рублей в банке под р% годовых. Через год он должен банку рублей.
- 20. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем
- 21. Если первоначальная сумма была х р., то через месяц эта сумма станет (х + 0,05х) р.
- 22. сумма увеличилась на , т.е. составляет от начальной Иначе говоря, она увеличилась по сравнению с начальной
- 23. k= m=1, n=3, t=2 . Срок хранения вклада равен k + m + n + t
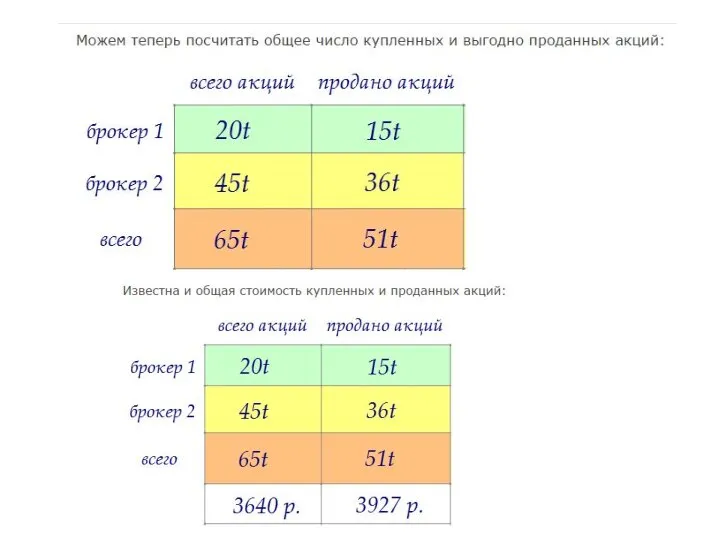
- 24. Два брокера купили акции одного достоинства на сумму 3640 р. Когда цена на эти акции возросла,
- 25. Обозначим число акций первого брокера (4х), (75% от этого числа равны (3х)). Обозначим число акций второго
- 29. Скачать презентацию














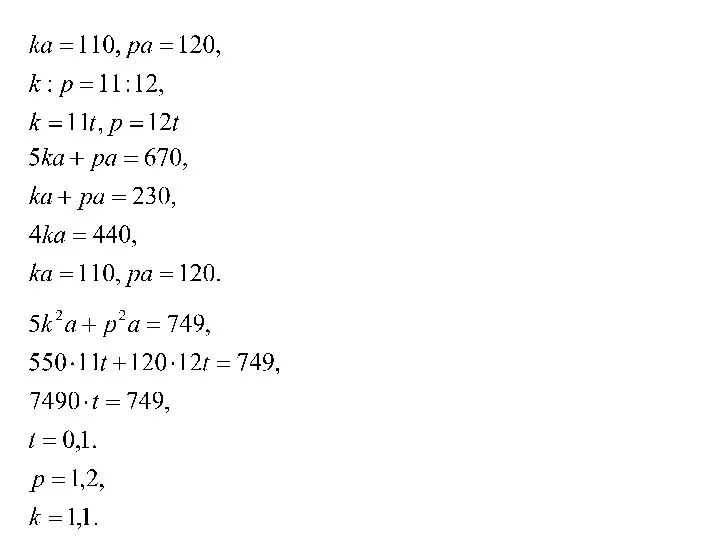










 Свойства функций
Свойства функций Классическое определение вероятности
Классическое определение вероятности Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша)
Темір жолдың жылжымалы құрамын пайдалану, жөндеу және техникалық қызмет көрсету (түрлері бойынша) Множества и отображения
Множества и отображения Цилиндр
Цилиндр Математический биатлон
Математический биатлон pril
pril Презентация на тему Подобие треугольников
Презентация на тему Подобие треугольников  Логарифмы
Логарифмы Лекция 5_1_СЛАУ_Итерац методы
Лекция 5_1_СЛАУ_Итерац методы Преобразование логарифмических выражений
Преобразование логарифмических выражений Упрощение выражений. Решение уравнений
Упрощение выражений. Решение уравнений Постер-фракталы для интерьера
Постер-фракталы для интерьера Задание на треугольники
Задание на треугольники Проверочная работа
Проверочная работа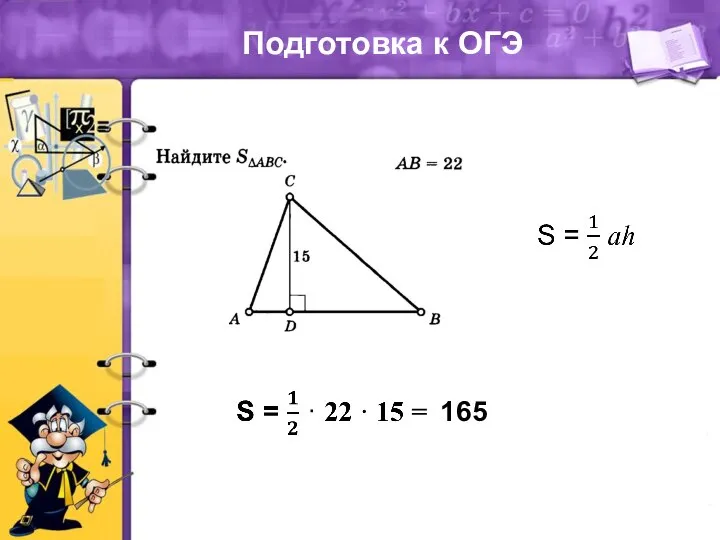 Теорема площади треугольника. Подготовка к ОГЭ
Теорема площади треугольника. Подготовка к ОГЭ Диаграммы Ламерея. Качественный анализ дискретных ДС
Диаграммы Ламерея. Качественный анализ дискретных ДС многогранники
многогранники Блиц-турнир по математике
Блиц-турнир по математике Письменное умножение на трёхзначное число
Письменное умножение на трёхзначное число Презентация на тему Подготовка к ЕГЭ по математике
Презентация на тему Подготовка к ЕГЭ по математике  Численные методы решения дифференциальных уравнений
Численные методы решения дифференциальных уравнений Презентация на тему Центральная и осевая симметрии в природе
Презентация на тему Центральная и осевая симметрии в природе  На что похож наш ноль?
На что похож наш ноль? Организация исследовательской деятельности учащихся по математике
Организация исследовательской деятельности учащихся по математике Презентация на тему Формулы квадрата суммы и квадрата разности двух выражений
Презентация на тему Формулы квадрата суммы и квадрата разности двух выражений  Что такое медиана?
Что такое медиана? Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений