Слайд 2Рассматривается краевая задача для системы двух уравнений второго порядка с разными степенями

малого параметра
f и g – достаточно гладкие функции.
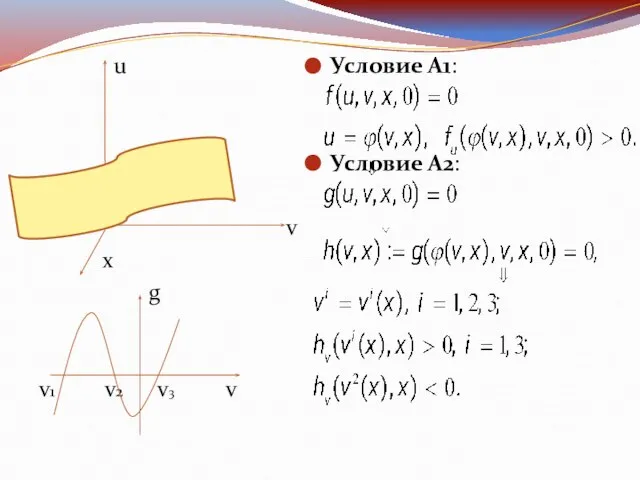
Слайд 3 u
v
x
g
v1 v2 v3 v
Условие А1:
Условие А2:
Слайд 4
Обозначим
Условие А3: Пусть существует - решение уравнения ,

причем
Слайд 5ОБРАТНАЯ КВАЗИМОНОТОННОСТЬ
Условие A4
всюду в области

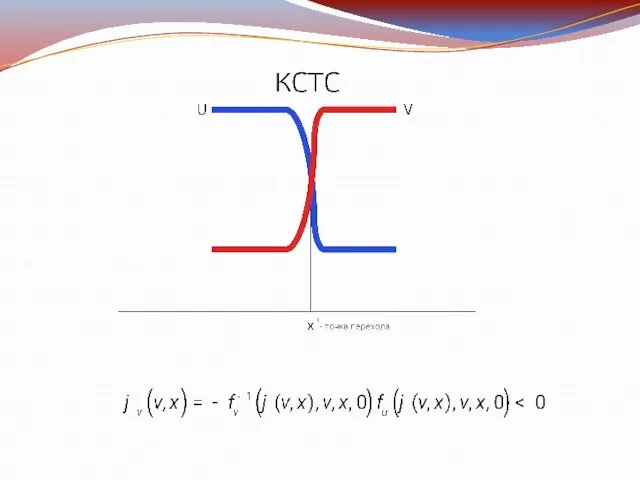
Слайд 7Асимптотика
Точка перехода:
Асимптотика решения задачи строится отдельно справа и слева от точки перехода

:
где
Слайд 8 Условия непрерывности асимптотического разложения v – компоненты решения в точке :
Условия

непрерывности производных асимптотических разложений в точке .
Слайд 9Регулярные члены асимптотики
Для функций получается вырожденная система:
Из условий У1 и У2 получаем:

Слайд 10Система уравнений для функций переходного слоя
(1)
(2)

Слайд 12Обоснование асимптотики
Теорема. При выполнении условий A1-A4 для достаточно малого существует решение задачи

, для которого функции являются равномерным на [0;1] асимптотическим приближением с точностью порядка
- построенная асимптотика n-ого порядка
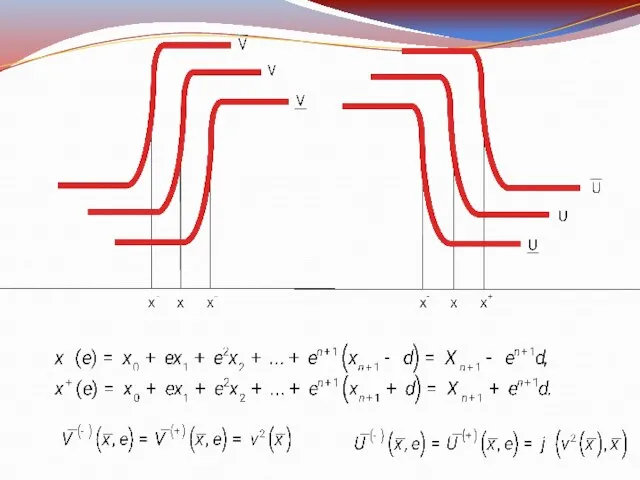
Слайд 18Определим функции как решения систем
уравнений
где A и B – положительные

числа.
Запишем решение системы:
где













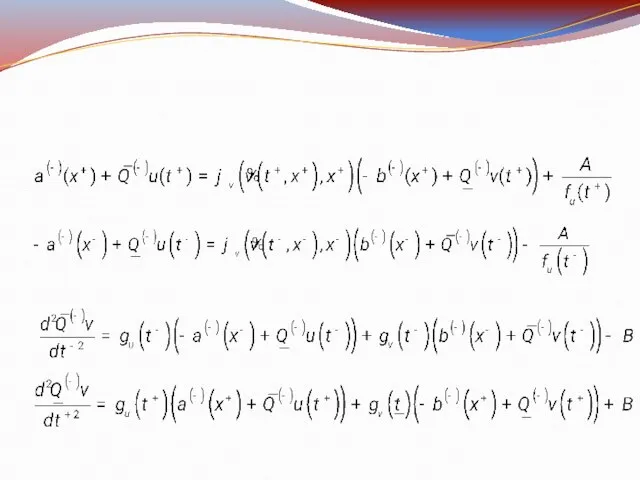


 Системы и совокупности неравенств с одной переменной
Системы и совокупности неравенств с одной переменной Квадрат. Свойства и признаки квадрата
Квадрат. Свойства и признаки квадрата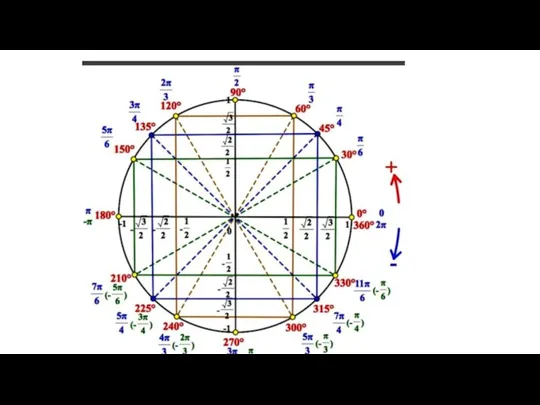 Тригонометрические функции
Тригонометрические функции Смежные и вертикальные углы
Смежные и вертикальные углы Признаки и свойства параллельных прямых
Признаки и свойства параллельных прямых Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 15
Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 15 Дифференциальное исчисление функции нескольких переменных
Дифференциальное исчисление функции нескольких переменных Решение задач на одновременное встречное движение
Решение задач на одновременное встречное движение Итерактивная мозаика
Итерактивная мозаика Презентация по математике "Дроби в Древнем Риме" -
Презентация по математике "Дроби в Древнем Риме" -  Отбор корней тригонометрического уравнения с помощью окружности
Отбор корней тригонометрического уравнения с помощью окружности Пространство и размерность
Пространство и размерность Розв'язання задач
Розв'язання задач Параллелограмм ауданы. 8сынып
Параллелограмм ауданы. 8сынып комбинаторика 1 лекция-1
комбинаторика 1 лекция-1 Метод линейного сплайна
Метод линейного сплайна Вычисление площадей фигур с помощью определенного интеграла
Вычисление площадей фигур с помощью определенного интеграла Неравенства. Тест
Неравенства. Тест Основное свойство дроби. Сокращение дробей
Основное свойство дроби. Сокращение дробей Теорема синусов
Теорема синусов Гипотеза Пуанкаре́
Гипотеза Пуанкаре́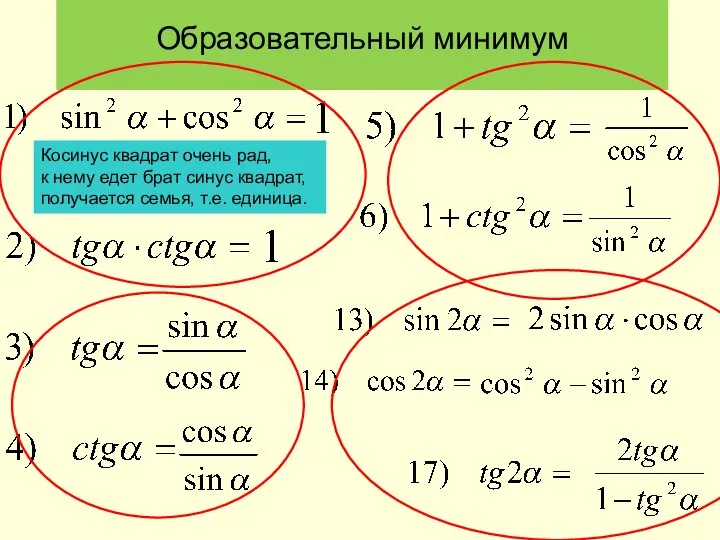 Образовательный минимум
Образовательный минимум Вычисление рациональным способом
Вычисление рациональным способом Взаимно-обратные задачи. 2 класс
Взаимно-обратные задачи. 2 класс Парная регрессия: линейный анализ
Парная регрессия: линейный анализ Отношения. Дискретная математика
Отношения. Дискретная математика Построение информационной модели метода изготовления изделия
Построение информационной модели метода изготовления изделия Расстояние от точки до прямой
Расстояние от точки до прямой