Методические рекомендации по изложению темы Площади плоских фигур по геометрии в 7 - 9 классах

Цель: найти методические приёмы, которые удовлетворяли бы требованиям научности изложения но, вместе с тем, имели бы элементы большей наглядности и простаты подачи материала.

Единицы измерения площади.
Площадь – одна из основных математических величин, характеризующая геометрические фигуры (реальные тела, объекты и т.п.). В простейших случаях площадь измеряется числом заполняющих плоскую фигуру единичных квадратов со стороной, равной единице длины. Квадрат со стороной 1 м является основной единицей измерения площади. Эта единица называется квадратный метр (м2).
1м
1м
Для измерения больших площадей (поверхности озёр, морей, территорий государств и т.д.) используют более крупную единицу 1 м площади – квадратный километр (км2). Малые поверхности (площади) измеряются квадратными сантиметрами (см2).

Нахождение площади прямоугольника.
Определение: Прямоугольник – это четырёхугольник, у которого все углы прямые, а противоположные стороны равны
A B
С D
SABCD = Sпрямоуг. = ab
Вывод: площадь прямоугольника равна произведению его длины на ширину.

Площадь квадрата.
Определение: квадрат – это прямоугольник, у которого все стороны равны
А B
C D
SABCD = Sквадр. = а*а = а2
Вывод: площадь квадрата равна квадрату его стороны.

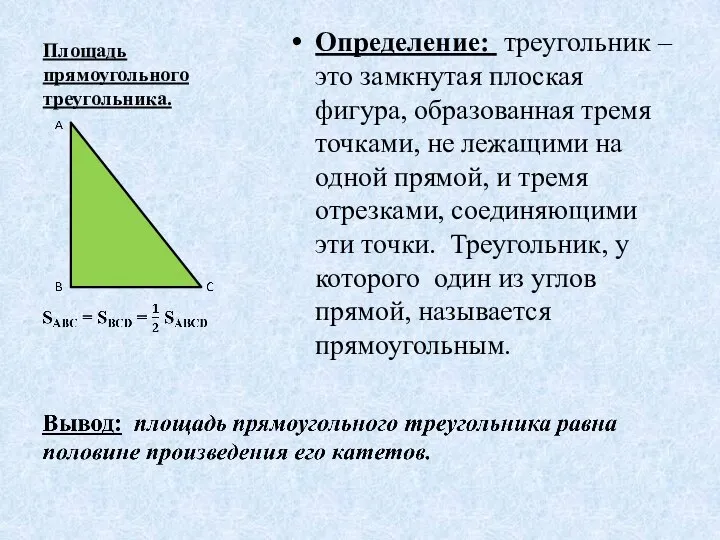
Площадь прямоугольного треугольника.
Определение: треугольник – это замкнутая плоская фигура, образованная тремя точками, не лежащими на одной прямой, и тремя отрезками, соединяющими эти точки. Треугольник, у которого один из углов прямой, называется прямоугольным.

Площадь произвольного треугольника.
Первый вариант
Пусть дан не прямоугольный разносторонний треугольник ABC со сторонами a, b, c (рис. 5). Опустим из вершины B на основание AC = a высоту BD = h. Высота BD разбивает треугольник на два прямоугольных треугольника ABD и BCD. Известно, что площадь фигуры равна сумме площадей частей, из которых она состоит. Следовательно, площадь треугольника ABC можно представить как сумму площадей треугольников ABD и BCD.

Площадь произвольного треугольника.

Площадь параллелограмма.
Определение: Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны.

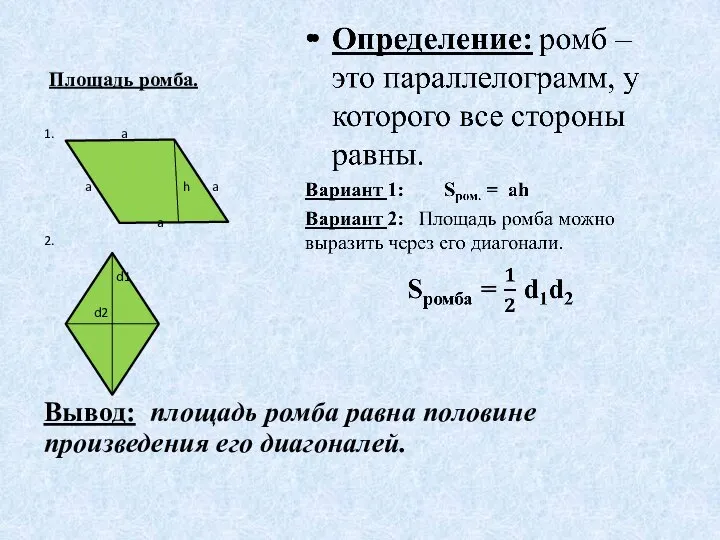
Площадь ромба.
1. a
a h a
a
2.
d1
d2
Вывод: площадь ромба равна половине произведения его диагоналей.

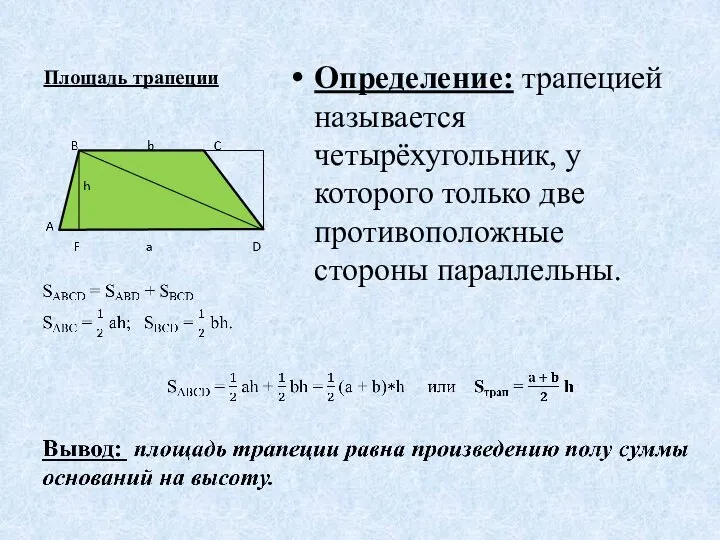
Площадь трапеции
Определение: трапецией называется четырёхугольник, у которого только две противоположные стороны параллельны.

Площадь круга.