Слайд 2Вычислить первообразные функции мы можем не всегда, но задача на дифференцирование может

быть решена для любой функции. Именно поэтому единого метода интегрирования, который можно использовать для любых типов вычислений, не существует.
Слайд 3Метод непосредственного интегрирования
Основной метод вычисления первообразной функции – это непосредственное интегрирование. Это

действие основано на свойствах неопределенного интеграла, и для вычислений нам понадобится таблица первообразных.
Слайд 4Пример непосредственного интегрирования

Слайд 5Метод замены переменной (метод подстановки)
Такой метод интегрирования заключается в выражении подынтегральной функции

через новую переменную, введенную специально для этой цели. В итоге мы должны получить табличный вид интеграла или просто менее сложный интеграл.
Этот метод очень полезен, когда нужно интегрировать функции с радикалами или тригонометрические функции.
Слайд 7Метод интегрирования по частям

Слайд 8Пример интегрирования по частям
Главная сложность применения такого метода – это необходимость выбирать,

какую часть брать за дифференциал, а какую – за функцию u(x).
Интегрирование по частям – метод для решения интегралов от произведения двух элементарных функций.








 Примеры арифметических операций
Примеры арифметических операций Презентация по математике "Праздник чисел «5 плюс »" -
Презентация по математике "Праздник чисел «5 плюс »" -  Презентация на тему Построение сечений тетраэдра
Презентация на тему Построение сечений тетраэдра  Арифметическая прогрессия
Арифметическая прогрессия Золотое сечение
Золотое сечение Игра Жизнь Conway's Game of Life
Игра Жизнь Conway's Game of Life Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота
Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота Круглые тела
Круглые тела Функція реакції
Функція реакції Построение треугольника
Построение треугольника Двугранный угол
Двугранный угол Тройные и многократные интегралы
Тройные и многократные интегралы Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Значение логического выражения (тема № 3)
Значение логического выражения (тема № 3) Таблица умножения трёх
Таблица умножения трёх Приближенные вычисления
Приближенные вычисления Производная сложной функции
Производная сложной функции 20b
20b Параллелепипед. Виды параллелепипедов
Параллелепипед. Виды параллелепипедов Разделительное свойство умножения
Разделительное свойство умножения Дискриминантный анализ
Дискриминантный анализ Пропорции. Проценты
Пропорции. Проценты Компьютерный и интеллектуальный анализ данных. Теория вероятностей
Компьютерный и интеллектуальный анализ данных. Теория вероятностей Интерактивный тренажёр Весёлый счёт. Математика 1 класс
Интерактивный тренажёр Весёлый счёт. Математика 1 класс Тела вращения
Тела вращения Логика. Задания
Логика. Задания Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира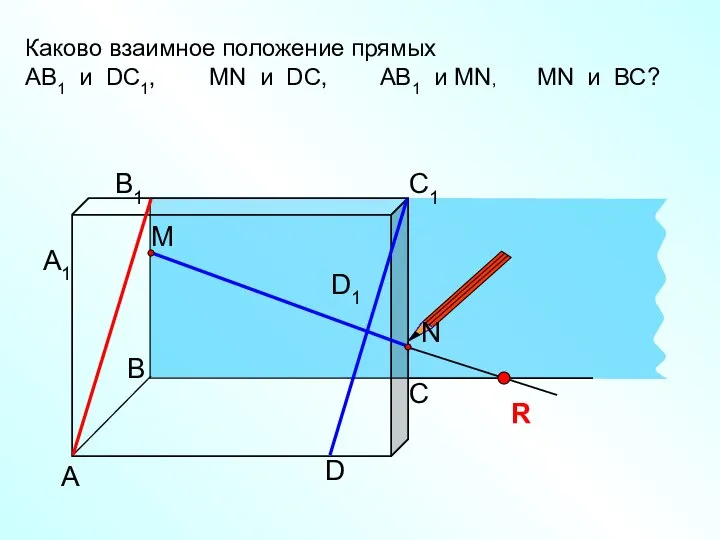 параллельность прямых и плоскостей 10
параллельность прямых и плоскостей 10