Первый признак равенства треугольников

К
В
С
1. <К противолежит сторона ВС
2. <К прилежат стороны КС и КВ
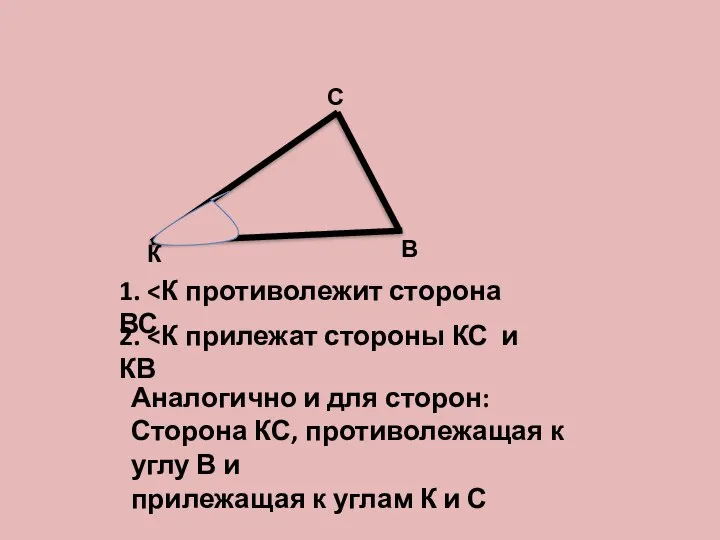
Аналогично и для сторон:
Сторона КС, противолежащая к углу В и
прилежащая к углам К и С

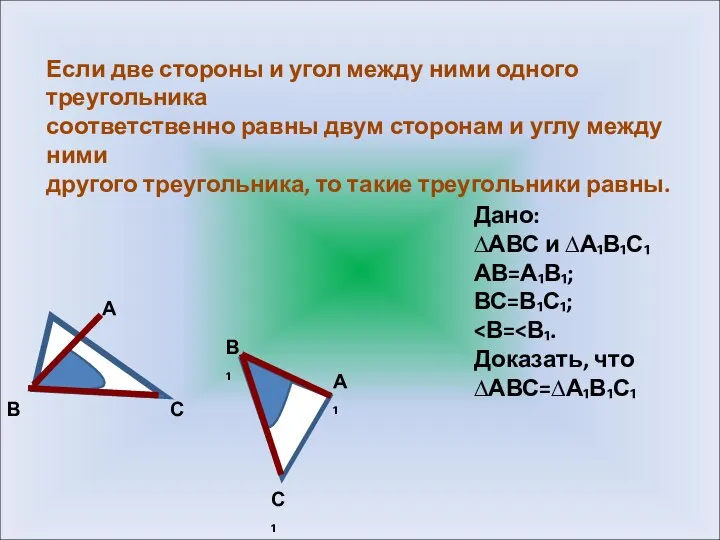
Если две стороны и угол между ними одного треугольника
соответственно равны двум сторонам и углу между ними
другого треугольника, то такие треугольники равны.
А
В
С
А₁
С₁
В₁
Дано:
∆АВС и ∆А₁В₁С₁
АВ=А₁В₁; ВС=В₁С₁;
<В=<В₁.
Доказать, что
∆АВС=∆А₁В₁С₁

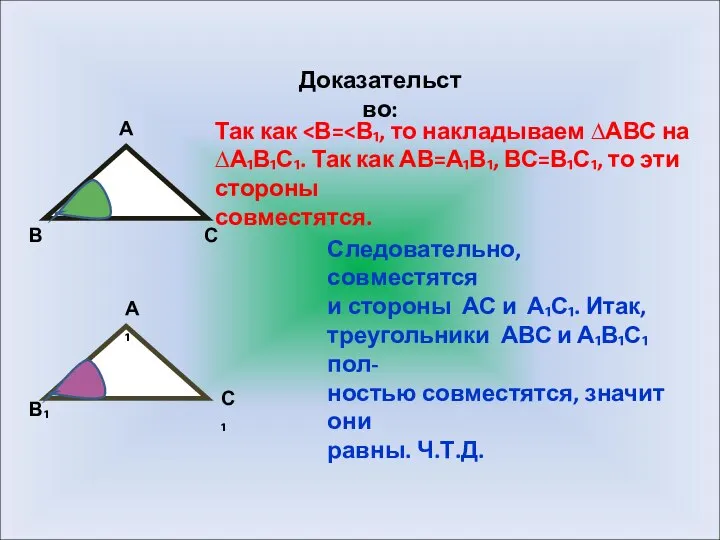
Доказательство:
В
С
А
А₁
С₁
В₁
Так как <В=<В₁, то накладываем ∆АВС на
∆А₁В₁С₁. Так как АВ=А₁В₁, ВС=В₁С₁, то эти стороны
совместятся.
Следовательно, совместятся
и стороны АС и А₁С₁. Итак,
треугольники АВС и А₁В₁С₁ пол-
ностью совместятся, значит они
равны. Ч.Т.Д.

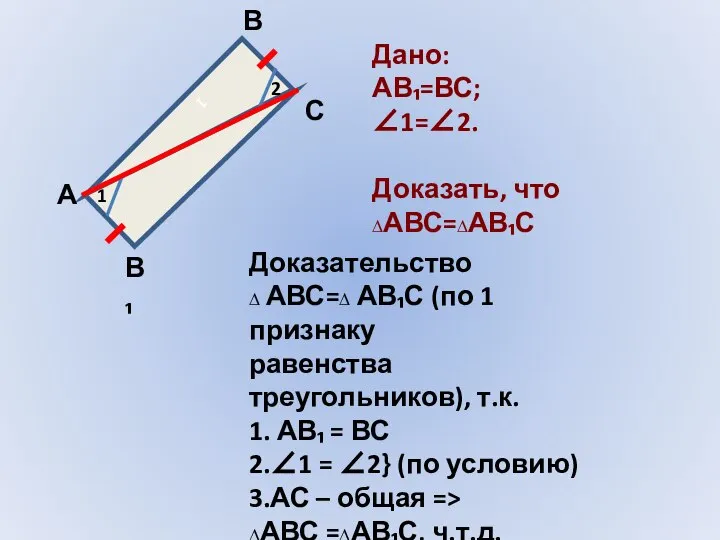
1
1
2
А
В
С
В₁
Дано:
АВ₁=ВС; ∠1=∠2.
Доказать, что
∆АВС=∆АВ₁С
Доказательство
∆ АВС=∆ АВ₁С (по 1 признаку
равенства треугольников), т.к.
1. АВ₁ = ВС
2.∠1 = ∠2} (по условию)
3.АС – общая =>
∆АВС =∆АВ₁С, ч.т.д.

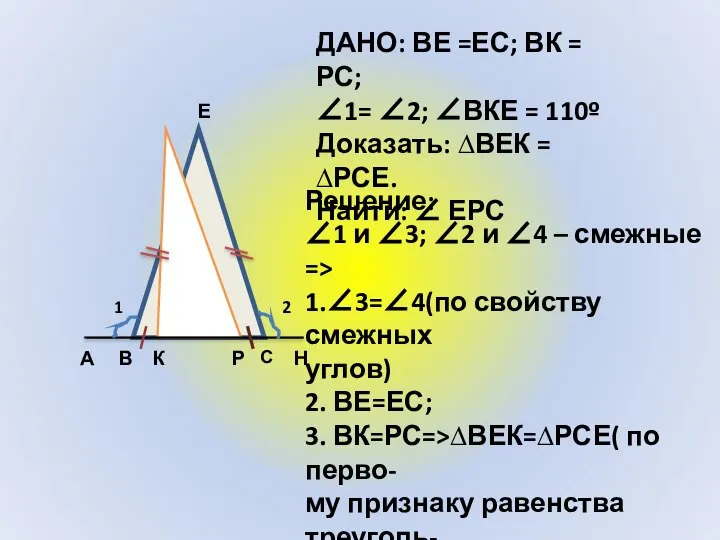
А
В
С
Н
К
Е
Р
1
2
ДАНО: ВЕ =ЕС; ВК = РС;
∠1= ∠2; ∠ВКЕ = 110º
Доказать: ∆ВЕК = ∆РСЕ.
Найти: ∠ ЕРС
Решение:
∠1 и ∠3; ∠2 и ∠4 – смежные =>
1.∠3=∠4(по свойству смежных
углов)
2. ВЕ=ЕС;
3. ВК=РС=>∆ВЕК=∆РСЕ( по перво-
му признаку равенства треуголь-
ников) ч.т.д.
∠ЕРС=∠ВКЕ=110° т.к.
∆ВЕК=∆РСЕ