Технология подготовки учащихся к овладению геометрическими методами решения задач с параметрами. Занятие №4
Содержание
- 2. Содержание курса 4
- 3. Содержание занятия О геометрических методах решения задач с параметрами Геометрический метод в задачах с параметром в
- 4. О геометрическом методе решения задач с параметром Задачи, решаемые этим методом, содержат «геометрический подтекст», поскольку их
- 5. О геометрических методах решения задач с параметрами Можно выделить два вида задач с параметрами, при решении
- 6. Геометрический метод в задачах с параметром в литературе для подготовки к ЕГЭ 2015 (проф. уровень) Геометрический
- 7. Геометрический метод в задачах с параметром в литературе для подготовки к ЕГЭ 2015 (проф. уровень)
- 8. Функционально-графические методы в электронных пособиях Прокофьева А.А. и Корянова А.Г. Адреса: http://alexlarin.net/ege/2012/C5-2012.http://alexlarin.net/ege/2012/C5-2012. html и http://www.alexlarin.net/ege/2011/c52011.html Из
- 9. Язык формул и расстояний «Алгебра – не что иное, как записанная в символах геометрия, а геометрия
- 10. Формула расстояния между двумя точками
- 11. Применение формулы расстояния между двумя точками на координатной оси
- 12. Язык расстояний на языке формул.-----------------
- 13. Язык расстояний на языке формул.-----------------
- 14. Язык формул на языке расстояний
- 15. Язык формул на языке расстояний
- 16. Язык формул на языке расстояний.
- 17. Соответствие формул и геометрических образов Рассмотрим соответствие некоторых уравнений, неравенств и просто выражений и их геометрических
- 18. Уравнение прямой Учебник. Шабунин М.И., Прокофьев А.А. Математика. Алгебра. Начала математического анализа. Проф. Уровень: учебник для
- 19. Задачи для самостоятельного решения 1 2
- 20. Системы двух линейных уравнений
- 21. Системы двух линейных уравнений
- 22. Система линейных неравенств
- 23. Соответствие формул и геометрических образов
- 24. Соответствие формул и геометрических образов
- 25. Соответствие формул и геометрических образов
- 26. Соответствие формул и геометрических образов
- 27. Соответствие формул и геометрических образов
- 28. Соответствие формул и геометрических образов
- 29. Расположение прямой и окружности
- 30. Пример из вариантов ЕГЭ 2011
- 31. Пример с «пучком прямых» (ЕГЭ 2013)
- 32. Использование уравнения окружности
- 33. Теоремы о взаимном расположении двух окружностей
- 34. Соответствие формул и геометрических образов
- 35. Соответствие формул и геометрических образов
- 36. Соответствие формул и геометрических образов
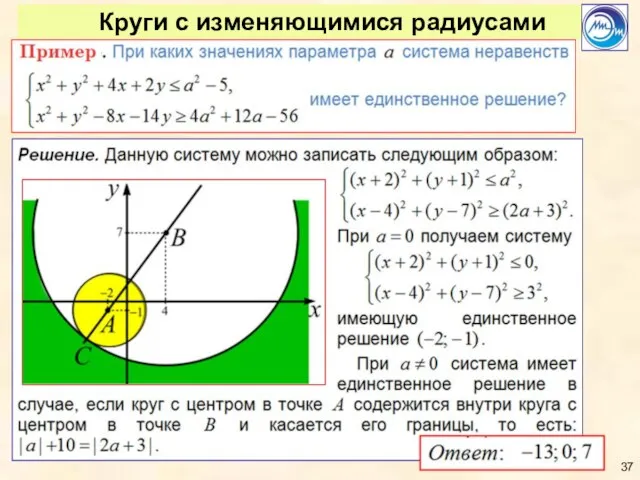
- 37. Круги с изменяющимися радиусами
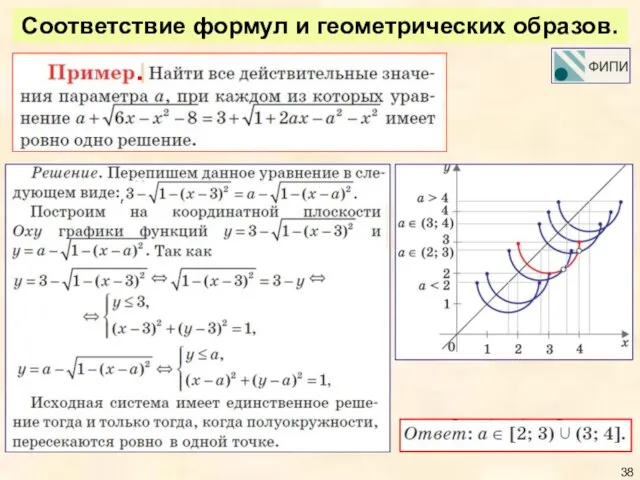
- 38. Соответствие формул и геометрических образов.
- 39. Соответствие формул и геометрических образов
- 40. Использование уравнения сферы
- 41. Задачи для самостоятельного решения 1 2 3
- 42. Соответствие формул и геометрических образов
- 43. Соответствие формул и геометрических образов
- 44. Соответствие формул и геометрических образов
- 45. Соответствие формул и геометрических образов
- 46. Соответствие формул и геометрических образов
- 47. Соответствие формул и геометрических образов
- 48. Окружность с изменяющимся радиусом
- 49. Задачи для самостоятельного решения 1 2
- 50. Соответствие формул и геометрических образов
- 51. Неравенство треугольника, уравнение отрезка
- 52. Для самостоятельной работы
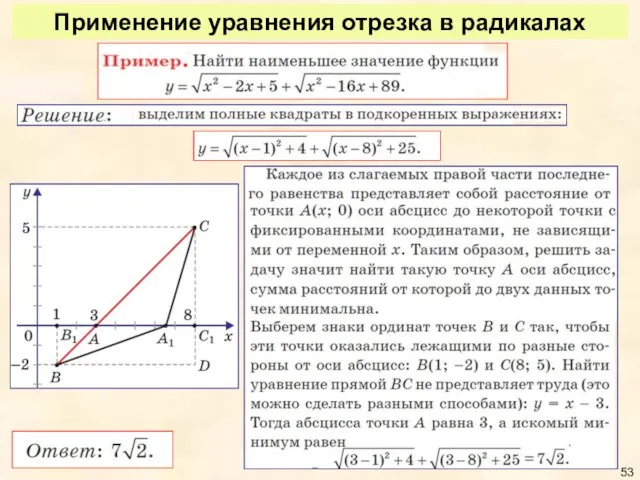
- 53. Применение уравнения отрезка в радикалах
- 54. Применение уравнения отрезка в радикалах
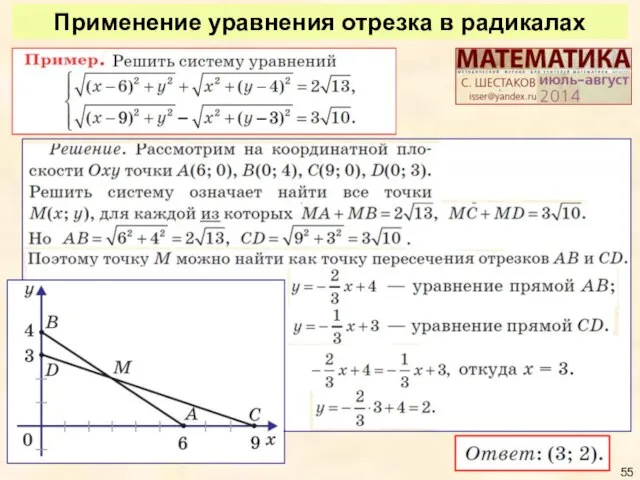
- 55. Применение уравнения отрезка в радикалах
- 56. Применение уравнения отрезка в радикалах
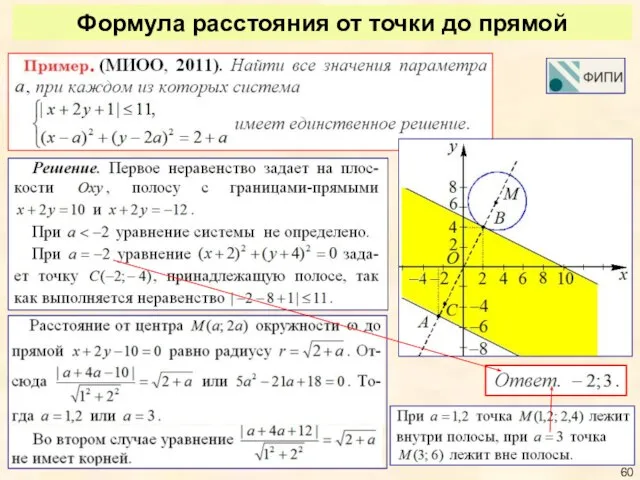
- 57. Формула расстояния от точки до прямой на плоскости
- 58. Формула расстояния от точки до прямой
- 59. Катится круг
- 60. Формула расстояния от точки до прямой
- 61. Векторные интерпретации в алгебре
- 62. Векторные интерпретации в алгебре ------------
- 63. Векторные интерпретации в алгебре ------------ Задача могла быть решена и с использованием формулы отрезка в радикалах
- 64. Векторные интерпретации в алгебре ------------
- 65. Векторные интерпретации в алгебре ------------
- 66. Задачи для самостоятельного решения
- 68. Задачи для осмысления
- 69. Площадь фигуры (задачи без параметра)
- 70. Площадь фигуры (задачи с параметром)
- 71. Площадь фигуры Шабунин М.И., Прокофьев А.А.
- 72. Параметры в геометрических задачах Задачи с параметрами в геометрии можно сгруппировать в задачи двух типов: 1)
- 73. Применение параметров в геометрии
- 79. Параметрические уравнения отрезка
- 80. Параметрические уравнения отрезка
- 81. Классификация задач, решаемых функционально-графическими методами
- 82. Печатные и электронные ресурсы Школьные учебники. Пособия для подготовки к ЕГЭ по математике. Журналы «Математика в
- 84. Скачать презентацию












































































 Предмет математика. Счёт предметов. Один, два, три…
Предмет математика. Счёт предметов. Один, два, три… Организация исследовательской деятельности учащихся на уроках математики
Организация исследовательской деятельности учащихся на уроках математики Длина окружности и площадь круга. 6 класс
Длина окружности и площадь круга. 6 класс Основные понятия теории вероятностей. Классическое определение вероятности и ее свойства. Правила
Основные понятия теории вероятностей. Классическое определение вероятности и ее свойства. Правила Презентация на тему Угол между прямыми
Презентация на тему Угол между прямыми  Презентация на тему Произведение чисел с разными знаками
Презентация на тему Произведение чисел с разными знаками  Измерение углов без транспортира
Измерение углов без транспортира Образование чисел из одного десятка и нескольких единиц. Урок №90
Образование чисел из одного десятка и нескольких единиц. Урок №90 Формування математчних моделей електронних кіл
Формування математчних моделей електронних кіл Свойства прямоугольных треугольников. Задачи
Свойства прямоугольных треугольников. Задачи Угол между векторами
Угол между векторами Решение задач по теме: Средняя линия треугольника. Пропорциональные отрезки в прямоугольном треугольнике
Решение задач по теме: Средняя линия треугольника. Пропорциональные отрезки в прямоугольном треугольнике Устойчивость движения, классификация точек покоя,
Устойчивость движения, классификация точек покоя, Как можно сравнивать размеры больших и малых тел
Как можно сравнивать размеры больших и малых тел Параллельность прямых
Параллельность прямых Теория вероятностей. Действия над вероятностями
Теория вероятностей. Действия над вероятностями Сравнительный анализ методов вычисления позиционных характеристик чисел в системе остаточных классов
Сравнительный анализ методов вычисления позиционных характеристик чисел в системе остаточных классов Вероятность события и ее свойства. Правила сложения и умножения вероятностей
Вероятность события и ее свойства. Правила сложения и умножения вероятностей Решение тригонометрических уравнений
Решение тригонометрических уравнений Метод простой итерации. Метод дихотомии
Метод простой итерации. Метод дихотомии Симметрия. Виды симметрии
Симметрия. Виды симметрии Продолжение решения задач на движение
Продолжение решения задач на движение 3_Equations_2
3_Equations_2 Поможем Буратино! Цель: формировать мыслительные операции
Поможем Буратино! Цель: формировать мыслительные операции Лекция+1+-+Предел+числовой+последовательности
Лекция+1+-+Предел+числовой+последовательности Решение задач на совместную работу и движение
Решение задач на совместную работу и движение Радианная мера угла. Синус, косинус, тангенс числа
Радианная мера угла. Синус, косинус, тангенс числа Расстояние между двумя точками. 9 класс
Расстояние между двумя точками. 9 класс