Методы общения линейных уравнений с тремя неизвестными

4.1. Решение систем линейных уравнений с
помощью обратной матрицы
(Матричный метод)
Матричный метод

Литература:
Линейная алгебра
Хамидуллин Р.Я. Гулиян Б.Ш.
Дома: теория - Занятие 4
Матричный метод

1. ОСНОВНЫЕ ПОНЯТИЯ.
Рассмотрим систему трёх линейных
уравнений с тремя неизвестными:
Матричный метод
где - неизвестные, - коэффициенты
( ),
- свободные члены.

Тройка чисел называется решением
системы трёх линейных уравнений с
тремя неизвестными, если при
подстановке их в уравнения системы
вместо получают верные
числовые равенства.
Матричный метод

Если система трёх линейных
уравнений имеет хотя бы одно
решение, то она называется
совместной.
Если система уравнений решений
не имеет, то она называется
несовместной.
Матричный метод

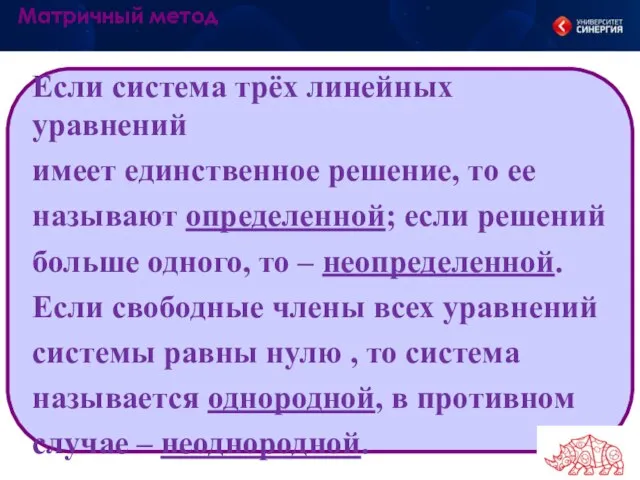
Если система трёх линейных уравнений
имеет единственное решение, то ее
называют определенной; если решений
больше одного, то – неопределенной.
Если свободные члены всех уравнений
системы равны нулю , то система
называется однородной, в противном
случае – неоднородной.
Матричный метод

ДАНО:
Матричный метод

В матричной форме записи
эта система уравнений имеет вид:
где:
А- основная матрица системы
Х-матрица неизвестных
В-матрица свободных членов
Матричный метод

Пусть
Тогда существует обратная матрица .
Если умножить обе части уравнения
на слева, то получим формулу для
нахождения неизвестных переменных, т.е.
Матричный метод

Подставим формулы: A-1∙A=E ; E∙X=X
Получим:
Матричный метод

Алгоритм решения системы линейных
уравнений в матричной форме.
1. Найти обратную матрицу
Найти произведение обратной матрицы
на столбец свободных членов:
3. Записать ответ.
3.1 Матричный метод

Пример.
Решите систему матричным
методом:
Матричный метод

Решение:
Матричный метод
Перепишем систему уравнений в матричном виде:
Так как определитель системы
Тогда систему трёх линейных уравнений с тремя неизвестными можно решить матричным методом.

Матричный метод
С помощью обратной матрицы решение этой системы может быть найдено так:
⬄

Построим обратную матрицу с помощью матрицы из алгебраических дополнений элементов матрицы А :
Матричный метод

Осталось вычислить матрицу неизвестных переменных, умножив обратную матрицу на матрицу свободных членов:
Ответ: .
Матричный метод

4.2. Решение систем линейных уравнений по формулам Крамера
Метод Крамера

Литература:
Линейная алгебра
Хамидуллин Р.Я. Гулиян Б.Ш.
Дома: теория - Занятие 4
решить -№ 2.1, стр.53
Теорема Крамера

Теорема Крамера
Система n уравнений с n неизвестными,
определитель которой не равен 0, всегда
имеет решение и притом единственное.
Оно находится так: каждое из
неизвестных равно дроби, знаменателем
которой является определитель
системы, а числитель получается из
определителя системы заменой столбца
при искомом неизвестном на столбец
свободных членов.
Теорема Крамера

Рассмотрим систему трёх линейных
уравнений с тремя неизвестными:
Теорема Крамера
где - неизвестные, - коэффициенты
( ),
- свободные члены.

Теорема Крамера

Рассмотрим случаи, когда определитель
системы равен нулю.
Теорема Крамера
Здесь возможны два варианта:
Δ=0 и каждый определитель Δхi = 0. Это имеет место тогда, когда коэффициенты при неизвестных Хi пропорциональны, т.е. каждое уравнение системы получается из первого уравнения умножением обеих его частей на число K.
Система уравнений имеет в этом случае бесчисленное множество решений.

Рассмотрим случаи, когда определитель
системы равен нулю.
Теорема Крамер
2. Δ=0 и хотя бы один из определителей Δхi ≠ 0. Это имеет место тогда, когда коэффициенты при всех неизвестных, кроме Хi пропорциональны. При этом получается система из противоречивых уравнений, которая не имеет решения.

Решите систему методом Крамера:
Решение: Вычислим определитель системы:
Так как определитель системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.
Теорема Крамера

Составим и вычислим необходимые определители :
Теорема Крамера

Находим неизвестные по формулам Крамера:
Теорема Крамера

4.3 Метод Гаусса
Метод Крамера можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является универсальным и пригоден для решения систем с любым числом уравнений. Рассмотрим систему трёх линейных уравнений с тремя неизвестными:
Метод Гаусса

Литература:
Линейная алгебра
Хамидуллин Р.Я. Гулиян Б.Ш.
Дома: теория - Занятие 4
Матричный метод

При решении систем линейных уравнений
используют метод Гаусса
(метод последовательного исключения
неизвестных).
Он состоит в следующем: систему
уравнений приводят к эквивалентной ей
системе с треугольной матрицей (системы
уравнений называются эквивалентными,
если множества решений их совпадают).
Эти действия называются прямым ходом.
3.3 Метод Гаусса

Из полученной треугольной
системы переменные находят
с помощью последовательных
подстановок (обратный ход)
3.3 Метод Гаусса

При выполнении прямого хода
используют следующие преобразования:
1.Перестановка двух строк;
2. Умножение строки на произвольное
число, отличное от нуля;
3. Прибавление к одной строке
другой строки, умноженной на
некоторое число;
4. Отбрасывание нулевой строки.
3.3 Метод Гаусса

Пример 1. Решить систему методом Гаусса:
Обозначим: Ав или А|В - расширенная матрица
системы.
Расширенная матрица этой системы имеет вид:
3.3 Метод Гаусса
.

Проведем следующие преобразования
расширенной матрицы системы: умножим
первую строку на -2 и сложим со второй
строкой (-2I+II) , а также умножим первую строку
на -1 и сложим с третьей строкой (-1I+III).
Результатом будет расширенная матрица первого
цикла (в дальнейшем все преобразования будем
изображать в виде схемы):
3.3 Метод Гаусса
.

Расширенная матрица этой системы имеет вид:
-3II+5III
3.3 Метод Гаусса
.

Полученная расширенная матрица соответствует
системе уравнений:
которая эквивалентна исходной системе.
Далее последовательно находим:
Проверкой убеждаемся, что система
решена верно
3.3 Метод Гаусса
.

Пример 2.Решить систему методом Жордана–Гаусса:
Расширенная матрица данной системы имеет вид:
3.3 Метод Гаусса
.

После первого шага по методу Гаусса получаем:
III:26 II+7III I+(-2)III
Метод Гаусса
.

Проделаем следующие операции: разделим
последнюю строку полученной матрицы на и,
умножив на 7 , прибавим ко второй строке,
умножив на –2 прибавим к первой строке.
Разделим вторую строку на 5 и прибавим к
первой, умножив на 2 .
II:5 I+2II
Метод Гаусса
.

Разделим вторую строку на 5 и прибавим к
первой, умножив на 2.
II:5 I+2II
Выписываем решение:
Метод Гаусса
.

Практикум :
1. Решить систему линейных уравнений с помощью обратной матрицы и методом Крамера.
Практикум