- Главная
- Математика
- Основатели теории вероятности и её значение на практике

Содержание
- 2. СОДЕРЖАНИЕ Введение 1.Теоретическая часть проекта 1.1 История и основатели теории вероятности 1.2 Области применения теории вероятности
- 3. ВВЕДЕНИЕ Теория вероятности встречается в нашей жизни каждый день, даже в тех вещах и отраслях жизни,
- 4. История и основатели теории вероятности В средние века люди стали задаваться вопросами, сколько возможных сумм очков
- 5. в 1477 году Бенвенуто д’Имола написал комментарий к «Божественной комедии» Данте, где шестой главе «Чистилища» упоминается
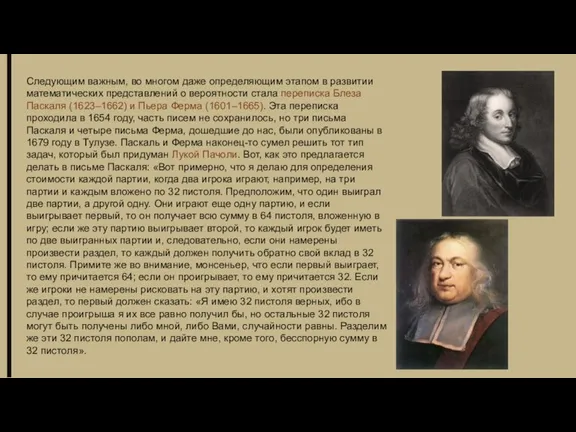
- 6. Следующим важным, во многом даже определяющим этапом в развитии математических представлений о вероятности стала переписка Блеза
- 7. Идея того, что вероятностные выкладки надо сопровождать математическим доказательством, последовательно проводилась русским математиком П. Л. Чебышевым
- 8. От теории вероятностей отпочковались и оформились в самостоятельные научные дисциплины: 1. Теория информации, предметом которой являются
- 9. Случайные и неслучайные события События бывают двух видов – случайные и неслучайные. Случайным событием называется то
- 10. Совместные, несовместные и противоположные события Случайные события тоже делятся на несколько групп. В этом подпункте поговорим
- 11. Комбинаторикой называется область математики, в которой изучают вопросы о том, сколько различных комбинаций, подчиненных тем или
- 12. Пример 1 Обычно торшеры выпускаются с одной большой лампой, которая может работать в трех режимах или
- 13. Пример 2 Если из двенадцати человек нужно выбрать комитет в составе девяти членов, то это можно
- 14. Теория вероятностей – интересный, пусть и в некоторых случаях непростой для понимания, раздел математики. Он связан
- 15. Вентцель Е.С. Теория вероятностей: Учебник для вузов. М.: Высшая школа, 2006г. Гмурман В.Е. Теория вероятностей и
- 17. Скачать презентацию
Слайд 2СОДЕРЖАНИЕ
Введение
1.Теоретическая часть проекта
1.1 История и основатели теории вероятности
1.2 Области применения теории вероятности
1.3
СОДЕРЖАНИЕ
Введение
1.Теоретическая часть проекта
1.1 История и основатели теории вероятности
1.2 Области применения теории вероятности
1.3

2.Практическая часть проекта
2.1 Комбинаторика и вероятность
Заключение
Список используемых источников
Слайд 3ВВЕДЕНИЕ
Теория вероятности встречается в нашей жизни каждый день, даже в тех вещах
ВВЕДЕНИЕ
Теория вероятности встречается в нашей жизни каждый день, даже в тех вещах

Это интереснейший раздел математики с долгой и увлекательной историей.
Цель:
Исследование теории вероятности с точки зрения истории и математики.
Задачи:
1.Разобраться, в каких областях исследований используется теория вероятности.
2.Узнать об ее основателях и истории происхождения.
Методы исследования:
Анализ учебных пособий и дополнительной литературы, решение задач.
Слайд 4История и основатели теории вероятности
В средние века люди стали задаваться вопросами, сколько
История и основатели теории вероятности
В средние века люди стали задаваться вопросами, сколько

Позднее французский священник, врач и поэт Ришар де Фурниваль (1201–1259) также написал труд об азартных играх, где говорил: «Одинаковое число очков на трех костях можно получить шестью способами. Если число очков на двух костях совпадает, а на третьей от него отлично, то мы имеем 30 способов, поскольку одна пара могла быть выбрана шестью способами, а третье число лишь пятью. Если очки на всех костях различны, то мы имеем 20 способов, поскольку 30 раз по 4 равно 120, но каждая возможность появляется шестью способами. Таким образом, существует всего 56 возможностей».
Слайд 5в 1477 году Бенвенуто д’Имола написал комментарий к «Божественной комедии» Данте, где
в 1477 году Бенвенуто д’Имола написал комментарий к «Божественной комедии» Данте, где

Слайд 6Следующим важным, во многом даже определяющим этапом в развитии математических представлений о
Следующим важным, во многом даже определяющим этапом в развитии математических представлений о
Слайд 7Идея того, что вероятностные выкладки надо сопровождать математическим доказательством, последовательно проводилась русским
Идея того, что вероятностные выкладки надо сопровождать математическим доказательством, последовательно проводилась русским

Слайд 8От теории вероятностей отпочковались и оформились в самостоятельные научные дисциплины:
1. Теория информации,
От теории вероятностей отпочковались и оформились в самостоятельные научные дисциплины:
1. Теория информации,

2. Теория массового обслуживания, изучающая закономерности систем для удовлетворения массового спроса в отдельном виде потребностей; основным понятием является требование (вызов, заявка и др.) – случайное событие, наступление которого вызывает необходимость в его обслуживании, например, вызов скорой помощи требует выезда к больному.
3. Теория надежности, занимающаяся методами обеспечения работы различных объектов в процессе их эксплуатации; в основе этой теории лежит понятие «отказ» – случайное событие, заключающееся в утрате работоспособности.
Области применения теории вероятности
Слайд 9Случайные и неслучайные события
События бывают двух видов – случайные и неслучайные. Случайным
Случайные и неслучайные события
События бывают двух видов – случайные и неслучайные. Случайным

Достоверные и невозможные события
Неслучайные события делятся на две группы – достоверные события и невозможные события. Достоверным событием называют то событие, которое обязательно произойдет. Такое событие обозначается буквой E. Невозможным событием называют то событие, которое в данных условиях произойти не может. Такое событие обозначается буквой U. Вероятность достоверного события всегда равна 1. Вероятность невозможного события всегда равна 0. Например, если из урны только с черными шарами вытащить шар, то достоверным событием будет то, что вытащенный шар окажется, черным. А невозможным событием будет то, что вытащенный шар окажется белым.
События и их классификация
Слайд 10Совместные, несовместные и противоположные события
Случайные события тоже делятся на несколько групп. В
Совместные, несовместные и противоположные события
Случайные события тоже делятся на несколько групп. В

Независимые и зависимые события
Существуют еще две группы случайных событий – независимые и зависимые события. Независимыми событиями называют события если, условная вероятность каждого из них равна безусловной вероятности.
Слайд 11Комбинаторикой называется область математики, в которой изучают вопросы о том, сколько различных
Комбинаторикой называется область математики, в которой изучают вопросы о том, сколько различных

Основной принцип комбинаторики
Основной принцип комбинаторики гласит: если что-либо одно можно осуществить m способами, а нечто другое – n способами, то эти действия последовательно можно осуществить m × n способами
Комбинаторика и вероятность
Слайд 12Пример 1
Обычно торшеры выпускаются с одной большой лампой, которая может работать в
Пример 1
Обычно торшеры выпускаются с одной большой лампой, которая может работать в

Любое размещение предметов, порядок которых не имеет значения, называется сочетанием. Из набора чисел 1, 2, 3, 4, 5 можно извлечь десятью различными способами любые два числа, если мы условимся не различать пары, состоящие из одних и тех же чисел, взятых в различном порядке, т. е. , например, не различать 1, 2 и 2, 1.
Слайд 13Пример 2
Если из двенадцати человек нужно выбрать комитет в составе девяти членов,
Пример 2
Если из двенадцати человек нужно выбрать комитет в составе девяти членов,

В общем случае число сочетаний из n по r равно n × (n – 1) × (n – 2) × (n – r + 1)/r! или n!/r! × (n – r)! Это число называется биномиальным коэффициентом. Еще один полезный принцип состоит в утверждении, что n предметов можно разложить в r коробок r × n различными способами, если в любой коробке может находиться любое число предметов. Чтобы убедиться в этом, заметим, что первый предмет можно положить в любую из r коробок, после чего второй предмет также можно положить в любую из r коробок и т. д. Таким образом, n предметов можно разложить способами.
Слайд 14Теория вероятностей – интересный, пусть и в некоторых случаях непростой для понимания,
Теория вероятностей – интересный, пусть и в некоторых случаях непростой для понимания,

Проделанная работа помогает разобраться в сущности теории вероятностей, научиться решать с помощью нее математические задачи, понять в каких областях она может применяться.
Заключение
Слайд 15Вентцель Е.С. Теория вероятностей: Учебник для вузов. М.: Высшая школа, 2006г.
Гмурман В.Е.
Вентцель Е.С. Теория вероятностей: Учебник для вузов. М.: Высшая школа, 2006г.
Гмурман В.Е.

Гнеденко Б.В. Очерк по теории вероятностей. М.: Эдиториал УРСС, 2009 г.
Майстров Л.Е. Развитие теории вероятностей. М.: Наука, 1980 г
Майстров Л.Е. Теория вероятностей. Исторический очерк. М.: Наука, 1967 г.
Булдык Г.М. Теория вероятностей и математическая статистика. - Мн.: Высшая школа, 1989 г.
Булдык Г.М., Ковальчук В.М. Теория вероятностей и математическая статистика. Практикум. Часть 1.- Мн.: БГЭУ, 1999 г.
Гороховик С.Я. Рыбалтовский И.В. Система случайных величин. Индивидуальные задания по теории вероятностей для студентов всех специальностей. – Мн.: БГЭУ, 2000 г.
Список используемых источников
 Правило чтения графиков
Правило чтения графиков Параллельность прямых и плоскостей (10 класс)
Параллельность прямых и плоскостей (10 класс) Понятие многогранника. Правильные многогранники
Понятие многогранника. Правильные многогранники Презентация на тему Решение неравенств с одним неизвестным
Презентация на тему Решение неравенств с одним неизвестным  Производная функции
Производная функции Презентация на тему Формирование и развитие УУД на уроках математики
Презентация на тему Формирование и развитие УУД на уроках математики  Призма. Виды призм
Призма. Виды призм Презентация на тему Квадратные уравнения. Основные свойства
Презентация на тему Квадратные уравнения. Основные свойства  Оценка вероятности поражения обслуживающего персонала при подрыве РКН
Оценка вероятности поражения обслуживающего персонала при подрыве РКН Презентация на тему Метр (2 класс)
Презентация на тему Метр (2 класс)  Свойства степени
Свойства степени Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира Решение задач модуля Геометрия
Решение задач модуля Геометрия Матрицы и определители
Матрицы и определители Презентация на тему Число 0. Цифра 0
Презентация на тему Число 0. Цифра 0  Платоновы тела
Платоновы тела Задачи на смекалку (ответы)
Задачи на смекалку (ответы) Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Сравнение чисел. Координаты
Сравнение чисел. Координаты Сравнительный анализ методов вычисления позиционных характеристик чисел в системе остаточных классов
Сравнительный анализ методов вычисления позиционных характеристик чисел в системе остаточных классов Презентация на тему Свойства степени с рациональным показателем
Презентация на тему Свойства степени с рациональным показателем  Учимся писать цифры
Учимся писать цифры Предел последовательности. Лекция 3
Предел последовательности. Лекция 3 Определение степени готовности объектов НКИ к применению. Тема 17
Определение степени готовности объектов НКИ к применению. Тема 17 Дроби вокруг нас
Дроби вокруг нас Доли и дроби Математика 5 класс Учитель Лебедева Т.Н.
Доли и дроби Математика 5 класс Учитель Лебедева Т.Н. Дифференциальные уравнения I порядка с разделяющимися переменными
Дифференциальные уравнения I порядка с разделяющимися переменными Нахождение числа по его дроби
Нахождение числа по его дроби