Слайд 2Взаимное расположение двух окружностей

Слайд 3Возможные случаи взаимного расположения окружностей

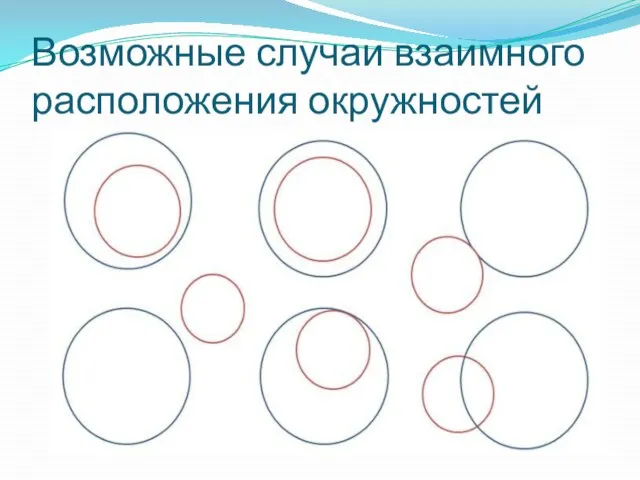
Слайд 4Возможные случаи взаимного расположения окружностей
Слайд 51. Центры окружностей совпадают
Такие окружности называются концентрическими. Если радиусы окружностей не равны, то

такие окружности образуют кольцо. Если радиусы окружностей равны, то окружности совпадают
Слайд 62. Центры окружностей не совпадают
Соединим центры прямой d, которую назовем линией центров
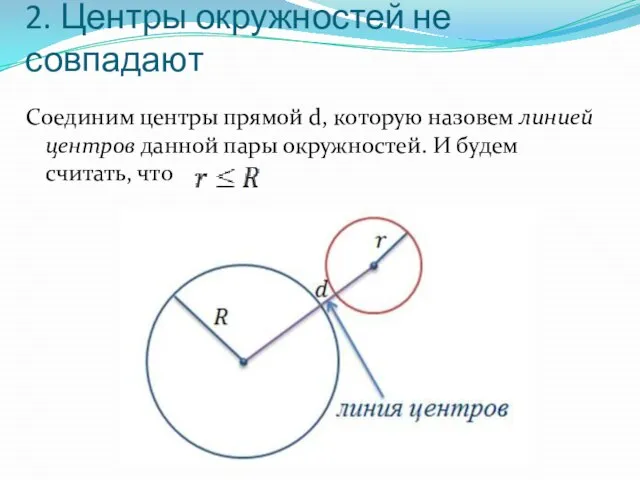
данной пары окружностей. И будем считать, что
Слайд 7Если , то очевидно, что окружности не пересекаются. В этом случае говорят,
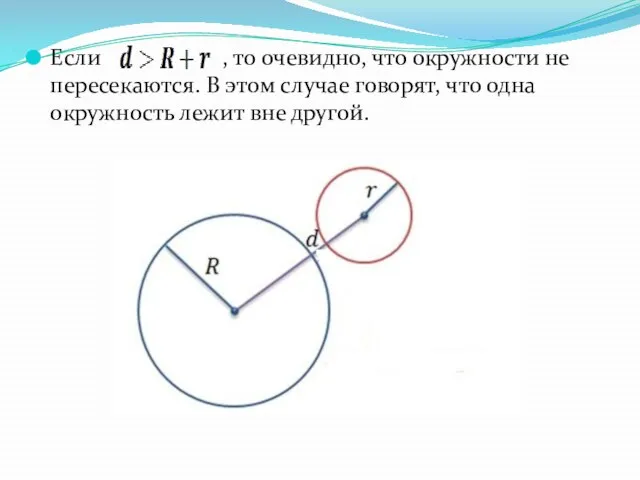
что одна окружность лежит вне другой.
Слайд 8Если , то тогда одна окружность лежит внутри другой, но они не
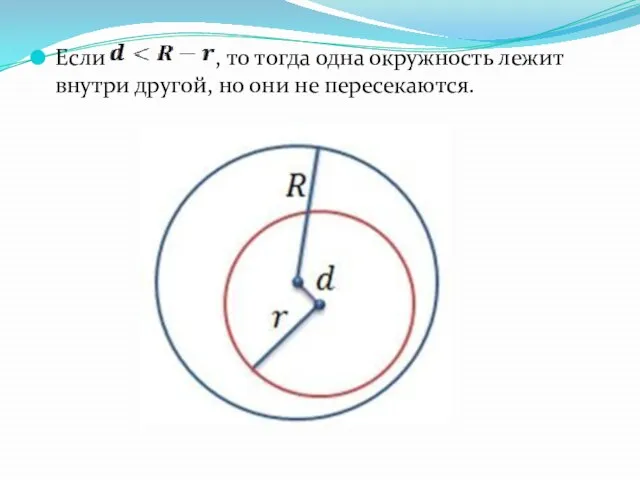
пересекаются.
Слайд 9Если , тогда малая окружность лежит внутри большой, но имеет с ней
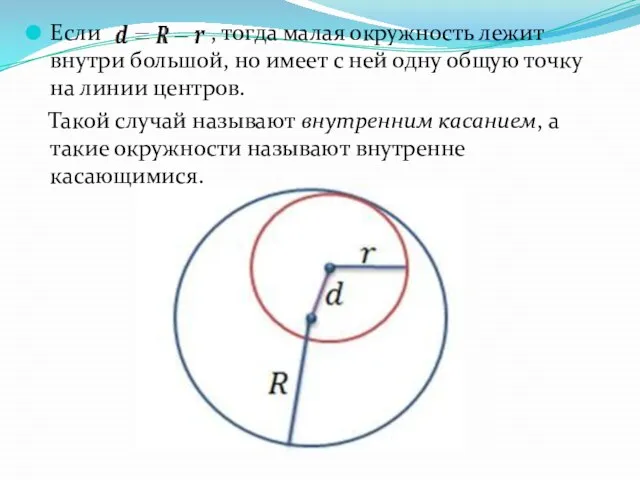
одну общую точку на линии центров.
Такой случай называют внутренним касанием, а такие окружности называют внутренне касающимися.
Слайд 10Если , то такие окружности имеют одну общую точку, причем центр одной

из них расположен за пределами второй окружности. Такой вид касания называется внешним касанием, а такие окружности называются внешне касающимися. Точка касания внешне касающихся окружностей лежит на линии центров.
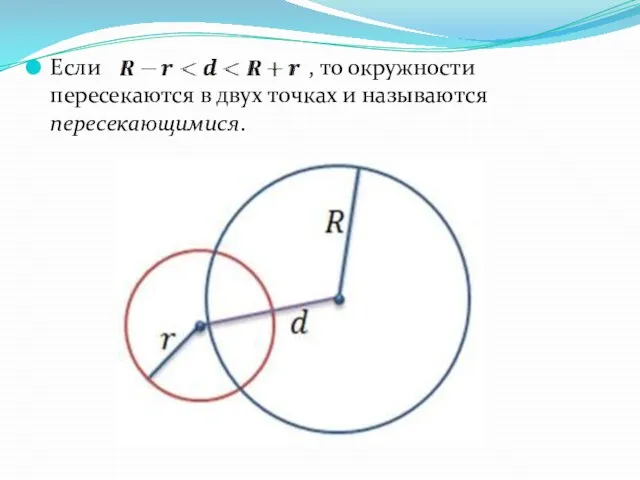
Слайд 11Если , то окружности пересекаются в двух точках и называются пересекающимися.
Слайд 12Домашнее задание:
стр. 238-240, п.96 разобрать;
№ 962, 969, устно разобрать № 981 и

письменно выполнить №983
В классе: № 971











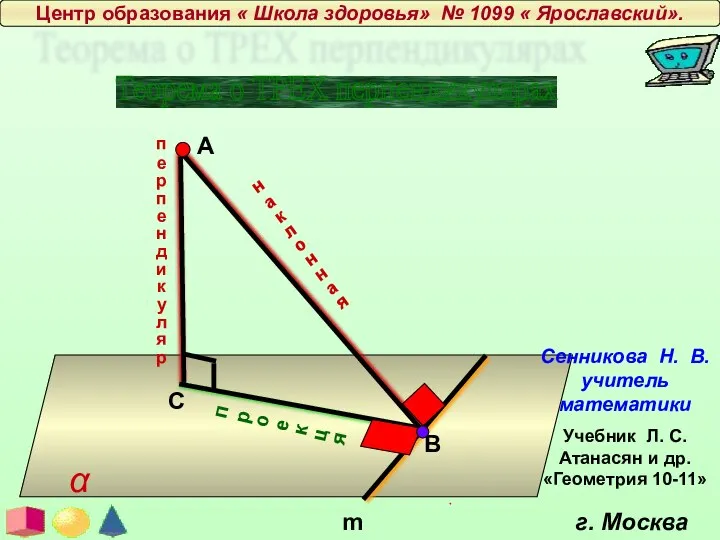 Теорема о трех перпендикулярах
Теорема о трех перпендикулярах Решение систем уравнений графическим и аналитическим способом
Решение систем уравнений графическим и аналитическим способом Презентация на тему Линейная функция (7 класс)
Презентация на тему Линейная функция (7 класс)  Векторы на плоскости. Понятие вектора. Равенство векторов
Векторы на плоскости. Понятие вектора. Равенство векторов Презентация на тему Волейбол. Передача сверху
Презентация на тему Волейбол. Передача сверху  Логические функции
Логические функции Состав чисел. Тренажер в программе PowerPoint
Состав чисел. Тренажер в программе PowerPoint Презентация на тему Свойства функций и их графики
Презентация на тему Свойства функций и их графики  Игра-тренажер Веселый счет
Игра-тренажер Веселый счет Взаимное расположение прямой и окружности (7 класс)
Взаимное расположение прямой и окружности (7 класс) Интерактивный тренажёр Реши уравнения
Интерактивный тренажёр Реши уравнения Множества
Множества Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Это забавные животные. Занимательные задачи
Это забавные животные. Занимательные задачи Задачи на координатной плоскости
Задачи на координатной плоскости Презентация на тему Сложение с переходом через десяток
Презентация на тему Сложение с переходом через десяток  Радианная мера угла. Поворот точки вокруг начала координат. Определение тригонометрических функций
Радианная мера угла. Поворот точки вокруг начала координат. Определение тригонометрических функций Оценки параметров распределения. Статистические оценки
Оценки параметров распределения. Статистические оценки Национальный стандарт по библиотечной статистике: преемственность и новые подходы
Национальный стандарт по библиотечной статистике: преемственность и новые подходы Прямая в пространстве R3. Лекция 6
Прямая в пространстве R3. Лекция 6 Выполни цепочку
Выполни цепочку Презентация на тему Параллелограмм и трапеция
Презентация на тему Параллелограмм и трапеция  Двугранный угол
Двугранный угол Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами
Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами Співвідношення між тригонометричними функціями
Співвідношення між тригонометричними функціями Транспортир Измерение углов Транспортир. История транспортира. Использование транспортира в жизни человека. Виды транспортир
Транспортир Измерение углов Транспортир. История транспортира. Использование транспортира в жизни человека. Виды транспортир Основное свойство пропорции
Основное свойство пропорции Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность