Метрология: применение математической статистики при измерениях и испытаниях

МЕТРОЛОГИЯ
Применение математической статистики
при измерениях и испытаниях

Статистические гипотезы. Проверка гипотез. Односторонний и двухсторонний критерии
Генеральная совокупность случайной величины (СВ) - бесконечное (очень большое) число наблюдений СВ.
Выборочная совокупность – выборка ограниченного объема из генеральной совокупности.

Закон распределения генеральной совокупности. Плотность распределения
- плотность непрерывного распределения
- непрерывная функция распределения
Х – случайная величина
- связь между функцией
и плотностью распределения

Статистическая гипотеза (СГ) – некоторое предположение относительно вида неизвестного или о параметрах известного распределения генеральной совокупности СВ.
Проверка СГ заключается
в сопоставлении неких статистических показателей (Θ - критериев проверки), вычисляемых по выборке,
со значениями Θкр. , которые определены при верной проверяемой гипотезе.

ЭТАПЫ ПРОВЕРКИ СГ
1 Выдвигают основную ( Н0 : )
и одновременно альтернативную ( Н1 : ) гипотезы.
2 Вычисляют по выборке СВ некий статистический критерий ( Θрасч. ) .
3 Сравнивают рассчитанное значение Θрасч. с критическим Θкр. (табличным).
4 В зависимости от результатов сравнения Θ > Θрасч.(Θ < Θрасч.) принимают Н0 : или Н1 :

Θрасч. - это специально подобранная CВ, точное или приблизительное распределение которой известно.
Проверка СГ заключается
в сопоставлении Θрасч.
со значением Θкр. , которое определено в предположении,
что проверяемая гипотеза верна.

Условия принятия (отбрасывания) гипотез:
1 Н0 : - принимается, если Θрасч. не попадает в критическую область, при этом отвергается Н1 :
2 Н1 : - принимается, если Θрасч. попадает в критическую область, одновременно отвергается Н0 :

Односторонний критерий принятия гипотезы
Для одностороннего (правостороннего) критерия вероятность попасть Θрасч.
в критическую область (заштрихована) равна Р (Θрасч.> Θкр.) = q
q - есть уровень значимости

Для левостороннего критерия вероятность попадания Θрасч.
в критическую область равна
Р (Θрасч.< Θкр.) = q
Вероятность попадания Θрасч.
в область принятия гипотезы Н0 равна α = 1- q
α - есть доверительная вероятность

Двухсторонний критерий принятия гипотезы
Вероятность попадания Θрасч.
в критическую область равна:
Р (Θрасч.< Θкр.1 ) + Р (Θрасч.> Θкр.2 ) = q

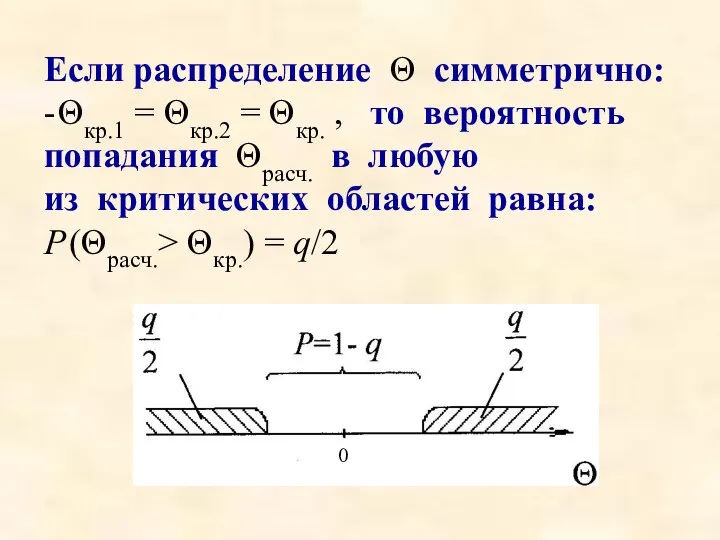
Если распределение Θ симметрично: - Θкр.1 = Θкр.2 = Θкр. , то вероятность попадания Θрасч. в любую
из критических областей равна:
Р (Θрасч.> Θкр.) = q/2
0

Для двухстороннего критерия численное значение q*/2 = 0,05
берут таким же, как для одностороннего критерия q = 0,05
В этом случае вероятность ошибки второго рода будет одинаковой для одностороннего и двухстороннего критерия (для последнего критерия получаем q*= 0,10 )
Практическое правило:

Как найти границы критической области ?
Рассмотрим правостороннюю область. Для нахождения Θкр. задаются малой вероятностью q (0,05; 0,025; 0,01) .
Затем ищут Θкр. ,
исходя из неравенства Р (Θ > Θкр.) = q

Это означает, что вероятность
события Θ > Θкр. мала,
и в единичном испытании оно
не должно наступить. Если все же событие произошло, то Н0 : ложна.

Ошибки первого и второго рода:
Ошибка 1-го рода – отвергнуть верную гипотезу (Н0 :) . Причем Н0 : действительно верна.
Её вероятность составляет не более q. При q = 0,05 ошибка 1-го рода произойдет в 5 случаях из 100. Ошибку 1-го рода называют
риском производителя

Ошибка 2-го рода – принять ложную гипотезу (Н0 :) за верную. Причем Н0 : действительно ложная. Оценить вероятность её очень сложно. При увеличении q , увеличивается число отвергаемых гипотез! Ошибку 2-го рода называют риском потребителя

Если вероятность ошибки 2-го рода принять равным β, то (1- β) называют мощностью критерия - это вероятность отклонения Н0 : , когда она ложная. Мощность критерия характеризует вероятность ошибочного применения ложной гипотезы Н0 .
1- β – вероятность не совершить ошибку второго рода.

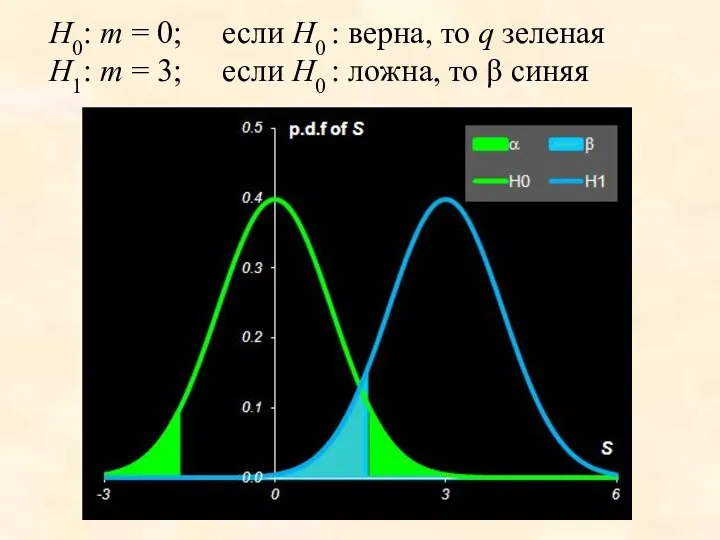
H0: m = 0; если H0 : верна, то q зеленая
H1: m = 3; если H0 : ложна, то β синяя

Мощность критерия должна быть максимальной, это обеспечивает минимальность ошибки 2-го рода.
Если уменьшать q , то β будет возрастать при n = const . Единственный способ одновременного уменьшения q и β - это увеличение объема выборки (n) !

Нормальный (гауссовский) закон распределения случайной величины
Карл Фридрих Гаусс 30.04.1777 - 23.02.1855 великий немецкий математик, астроном и физик. Считается одним из величайших математиков всех времён «Король математиков»

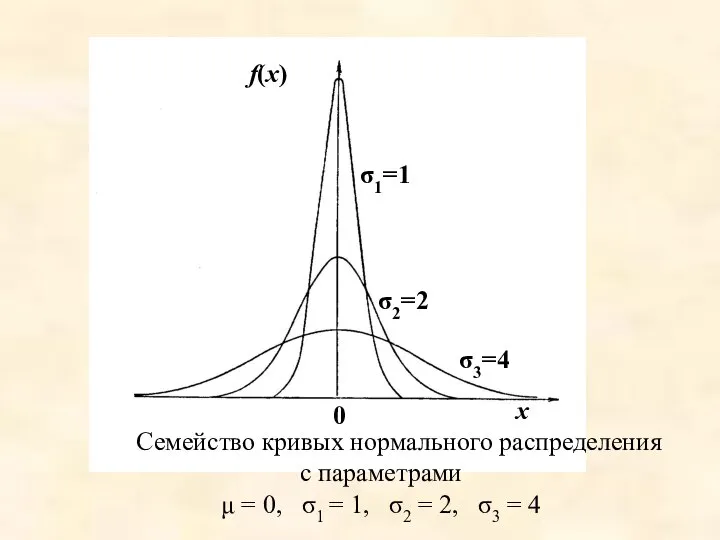
– генеральное мат. ожидание СВ
σ 2 – генеральная дисперсия СВ
СВ распределена по нормальному закону, если плотность её распределения описывается выражением:

Характеристики кривой НР:
1 Симметрия относительно центра распределения: Медиана равна мат. ожиданию
2 Мода – в центре распределения
3 f ( x ) > 0
4 Точки перегиба – при

Вычисление вероятности
по нормальному закону распределения
Пусть случайная величина Х распределена по нормальному закону, тогда вероятность найти Х < х равна:

Перейдем к интегралу вероятности
- центрирование, нормировка, замена переменной
→ из свойства F(x)

- функция Лапласа
Свойства функции Лапласа:
нечетная функция

Пьер-Симо́н, маркиз де Лапла́с (Pierre-Simon de Laplace)
23.03.1749-05.03.1827. Французский математик, механик, физик
и астроном. Известен работами в области небесной механики, диф.уравнений, один из создателей теории вероятности. Заслуги Лапласа в области теоретической
и прикладной математики
и, особенно в астрономии, громадны: он усовершенствовал почти все отделы этих наук.
Был членом Французского географического общества.

Таблица значений функции

Вычисление вероятности нахождения СВ, распределенной
по НЗ, в интервале от a до b
по функции (интегралу) Лапласа

Заменим СВ х по НЗ на
получим
Если генеральные МО и дисперсия известны, то вероятность найти “ х ”
в интервале (a, b) :

Перейдем от “ x ” к отклонению от мат.ожидания ,
и переформулируем задачу:
где

Если интервал (А, В) симметричен: A= – B и В > 0 , т.к. Ф(х) - нечетная:
Тогда вероятность найти:
(1)

Пример 1: вычислим по (1) какова вероятность, что , т.к. В ≡ σ ,
то есть аргумент
При n→∞ в 2/3 наблюдений не превышает σ !!!

Пример 2: вычислим какова вероятность, что , т.е.
Пример 3: вычислим вероятность,
что , т.е.
Это правило 1, 2 и 3 σ !!!