Содержание
- 2. Многогранники МНОГОГРАННИК – ЭТО ТЕЛО, ГРАНИЦА КОТОРОГО СОСТОИТ ИЗ КУСКОВ ПЛОСКОСТЕЙ ( МНОГОУГОЛЬНИКОВ ). ЭТИ МНОГОУГОЛЬНИКИ
- 4. призма параллелепипед Усечённая пирамида пирамида
- 5. Тела Кеплера-Пуансо
- 6. пять удивительных многогранников
- 7. Их изучали ученые, ювелиры, священники, архитекторы. Этим многогранникам даже приписывали магические свойства. Древнегреческий ученый и философ
- 8. Тетраэдр Правильный четырёхгранник у которого грани правильные треугольники, в каждой вершине сходится по 3 ребра и
- 9. Куб — шесть граней — равные квадраты. Куб имеет восемь вершин и двенадцать ребер.
- 10. Октаэдр — восемь граней — равносторонние равные треугольники. Октаэдр имеет шесть вершин и двенадцать ребер
- 11. Додекаэдр — двенадцать граней — правильные равные пятиугольники. Додекаэдр имеет двадцать вершин и тридцать ребер.
- 12. Икосаэдр — двадцать граней — равносторонние равные треугольники. Икосаэдр имеет двенадцать вершин и тридцать ребер.
- 13. Сечения многогранников Правила построения сечений многогранников: 1) проводим прямые через точки, лежащие в одной плоскости; 2)
- 14. сечения
- 15. ВАЖНО! ДЛЯ ПОСТРОЕНИЯ СЕЧЕНИЙ ИЩЕМ ОТРЕЗКИ, ПО КОТОРЫМ СЕКУЩАЯ ПЛОСКОСТЬ ПЕРЕСЕКАЕТ КАЖДУЮ ГРАНЬ. МОЖНО СОЕДИНЯТЬ ТОЛЬКО
- 16. Решение. 1. Построим след секущей плоскости на плоскость нижнего основания призмы. Рассмотрим грань АА1В1В. В этой
- 17. Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построим сечение, проходящее через точки M, N, L.
- 18. Соединим точки M и L, лежащие в плоскости AA1D1D.
- 19. Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим
- 20. Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей
- 21. Найдем прямую пересечения плоскости сечения с плоскостью DD1C1C: пересечем прямую ML (принадлежащую сечению) с ребром DD1,
- 22. пересечем прямую KN (принадлежащую сечению) с ребром D1C1, они лежат в одной плоскости A1B1C1D1, получим точку
- 24. Скачать презентацию

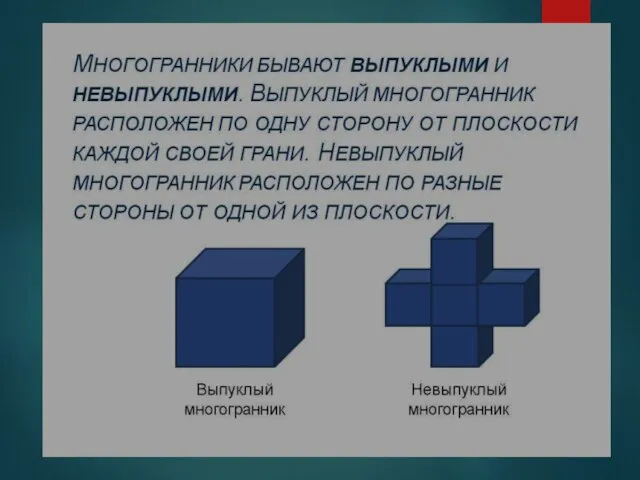
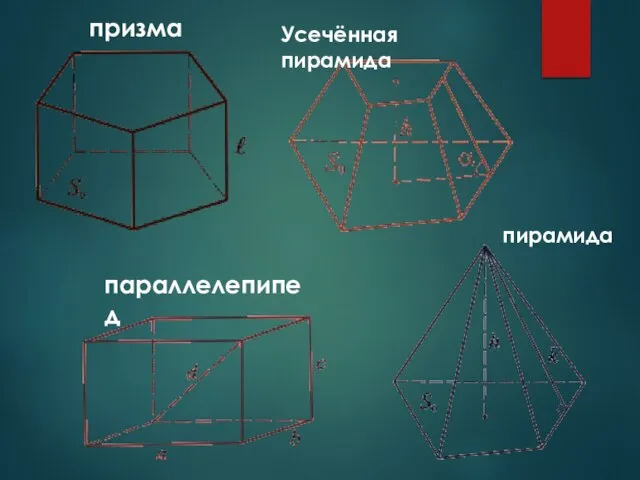
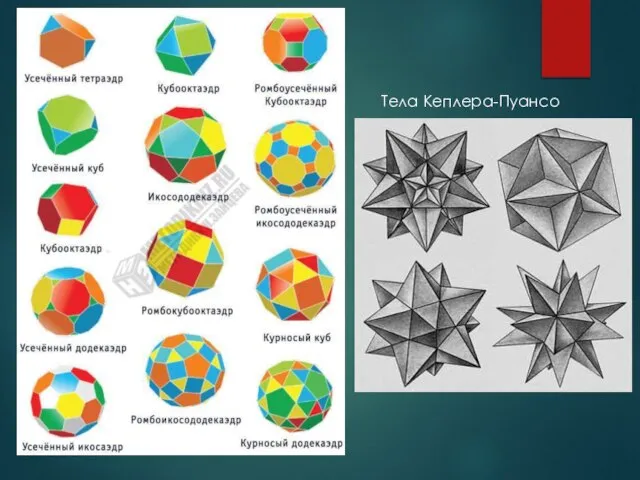
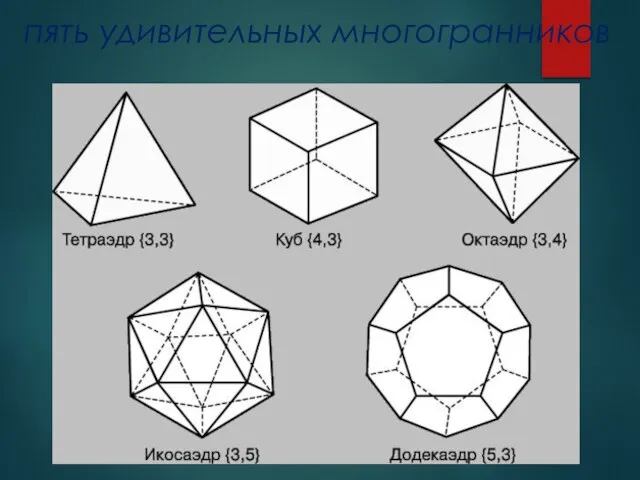

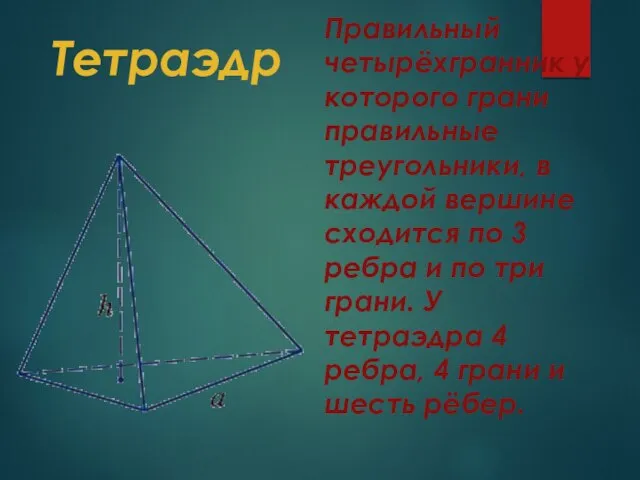
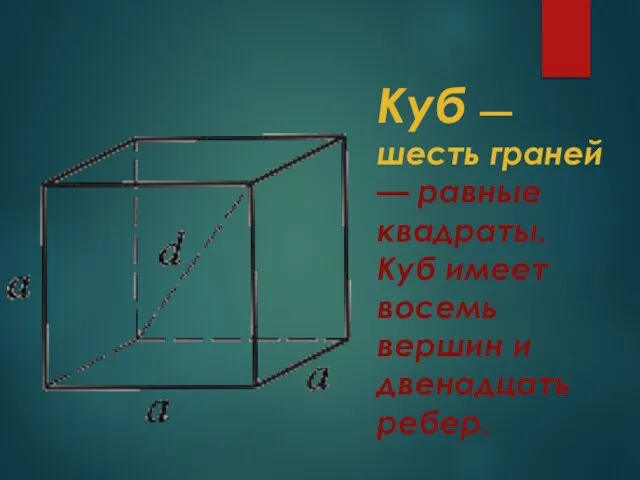
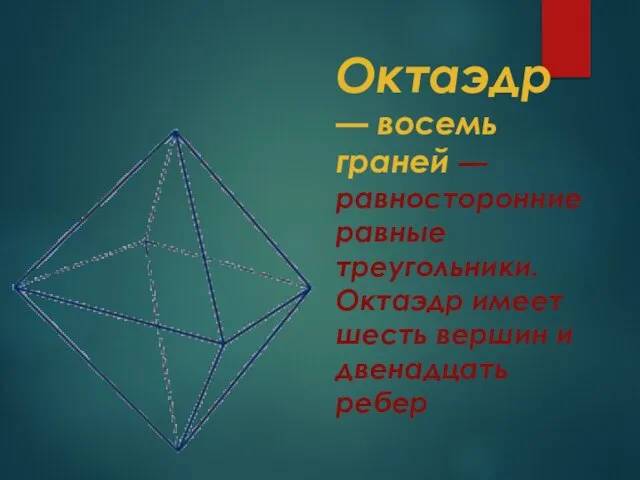
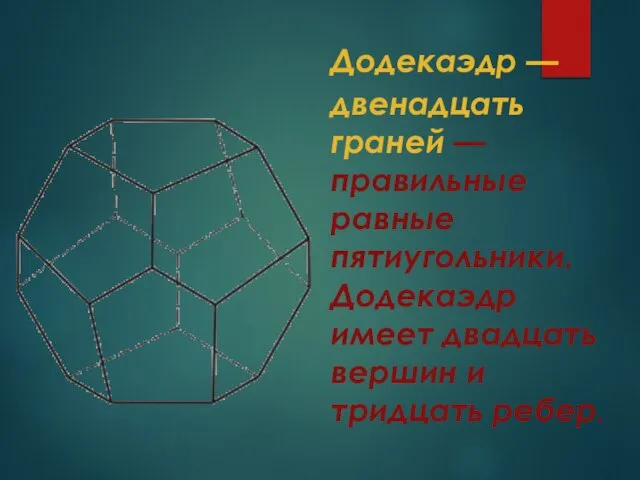
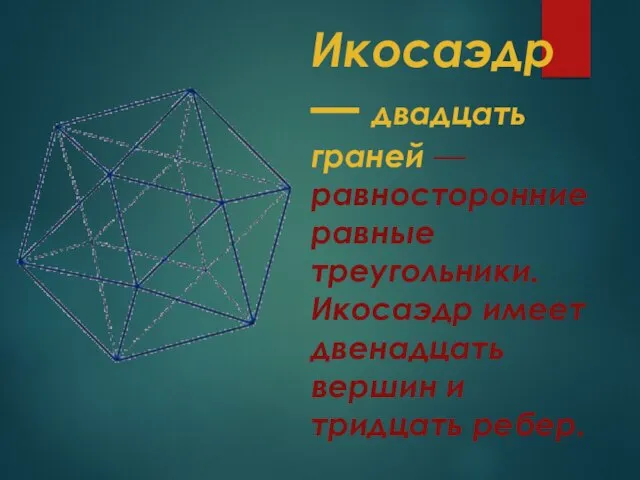

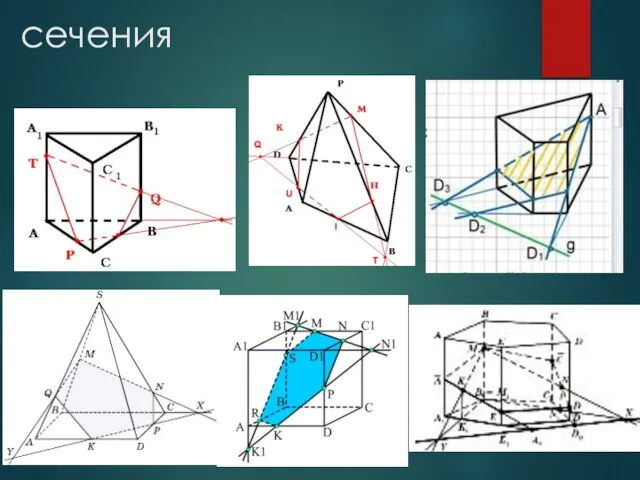



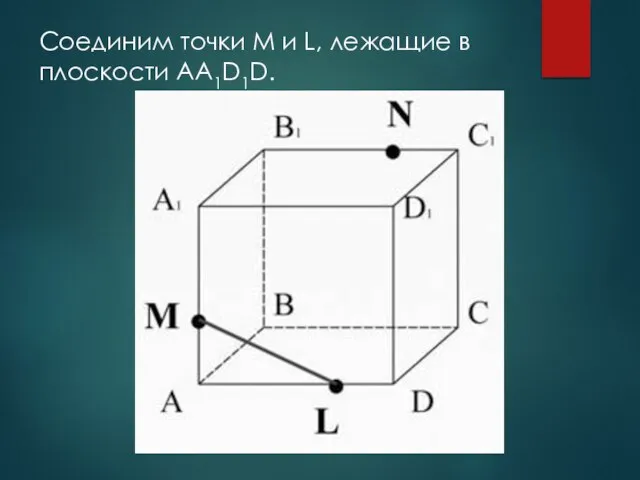
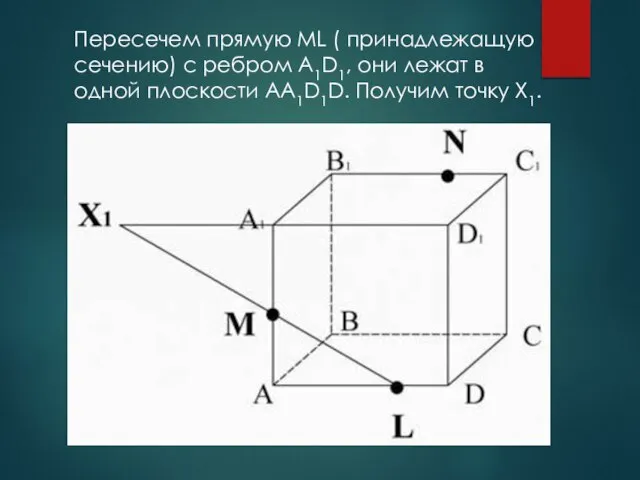
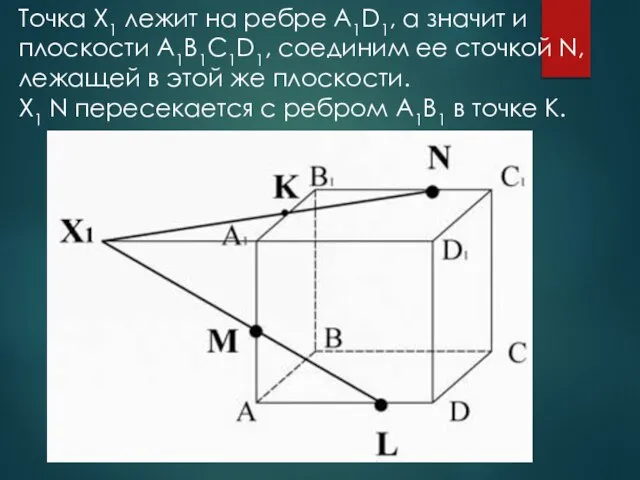
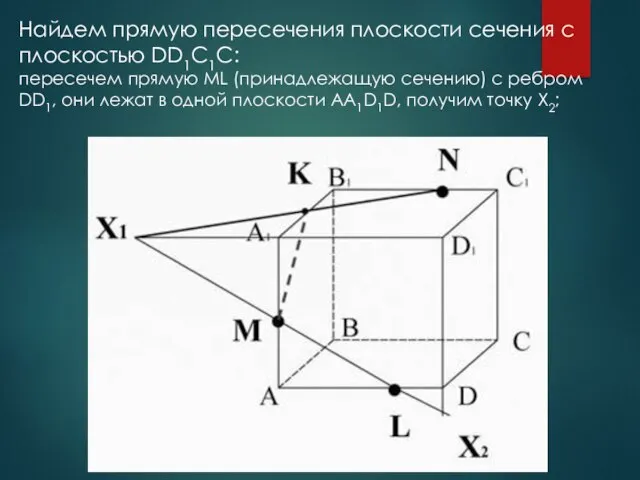
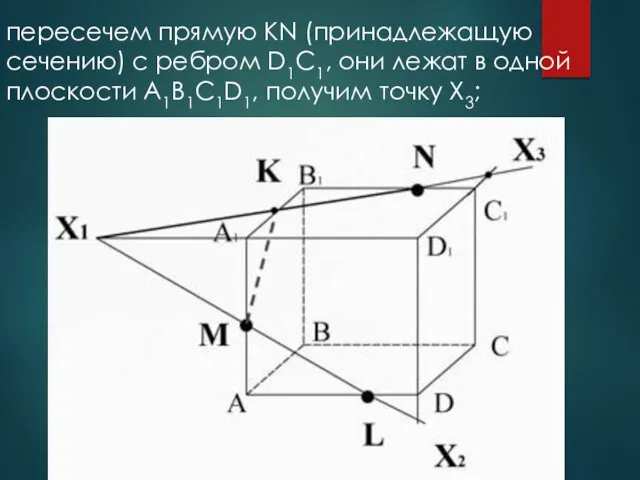
 Таблица сложения
Таблица сложения Группы по одному или нескольким признакам
Группы по одному или нескольким признакам Алгоритмы решения простейших тригонометрических неравенств
Алгоритмы решения простейших тригонометрических неравенств Прямоугольный треугольник
Прямоугольный треугольник Презентация на тему Угол между прямыми. Угол между прямой и плоскостью
Презентация на тему Угол между прямыми. Угол между прямой и плоскостью  Перпендикулярности прямой и плоскости
Перпендикулярности прямой и плоскости Интерактивный пазл
Интерактивный пазл Приём вычисления для случаев вида 36+2, 36+20. Задание 1
Приём вычисления для случаев вида 36+2, 36+20. Задание 1 Решение задач всех типов на обыкновенные дроби
Решение задач всех типов на обыкновенные дроби Соотношения между тригонометрическими функциями одного и того же аргумента
Соотношения между тригонометрическими функциями одного и того же аргумента Декартова система координат в пространстве
Декартова система координат в пространстве Предел последовательности. Бесконечно убывающая геометрическая прогрессия
Предел последовательности. Бесконечно убывающая геометрическая прогрессия Применение комплексных чисел на практике
Применение комплексных чисел на практике Разные способы нахождения площади многоугольников. Обобщающее повторение при подготовке к ЕГЭ по математике
Разные способы нахождения площади многоугольников. Обобщающее повторение при подготовке к ЕГЭ по математике Ньютон и Лейбниц – создатели математического анализа
Ньютон и Лейбниц – создатели математического анализа Решение уравнений
Решение уравнений Алгебраический способ решения задач (часть 1)
Алгебраический способ решения задач (часть 1) Ситуация успеха на уроках математики как средство повышения качества образования
Ситуация успеха на уроках математики как средство повышения качества образования Геометрия вокруг нас
Геометрия вокруг нас Задачи на построение сечений
Задачи на построение сечений Признаки параллельности прямых
Признаки параллельности прямых Обыкновенная дробь. 6 класс
Обыкновенная дробь. 6 класс Мир глазами эколога
Мир глазами эколога Комбинаторика. 11 класс
Комбинаторика. 11 класс Основные тригонометрические тождества. Преобразование тригонометрических выражений
Основные тригонометрические тождества. Преобразование тригонометрических выражений Кратное сравнение
Кратное сравнение Элективный курс «Математическая статистика и теория вероятностей» Образовательная область «Математика» Лактионова Н.С.
Элективный курс «Математическая статистика и теория вероятностей» Образовательная область «Математика» Лактионова Н.С. 08.09
08.09