Содержание
- 2. Лекция 6. Математические основы ТАУ (продолжение). План лекции: Дифференциальные уравнения Передаточные функции Временные характеристики Частотные характеристики.
- 3. 1. Дифференциальные уравнения. Существуют следующие формы математического описания динамических свойств линейных звеньев и систем: дифференциальные уравнения
- 4. Математическая связь между выходной и входной величинами и их производными по времени для большинства тепловых объектов
- 5. В качестве примера составим дифференциальное уравнение для системы: в бак поступает жидкость в количестве Q1 и
- 6. На основе этого можно составить уравнение материального баланса для данной системы: S ∙ Δh = (Q1
- 7. При малых отклонениях Δh можно нелинейную зависимость заменить линейной, т.е. Q2 (t) ≈ α ∙ h
- 8. Если при составлении уравнений системы принимаются во внимание все факторы, влияющие на динамику процесса управления, то
- 9. 2. Передаточные функции. Линейные дифференциальные уравнения САУ решаются различными методами, но для решения задач в ТАУ
- 10. Существует прямое и обратное преобразование Лапласа: прямое – операция перехода от исходной функции у(t) к ее
- 11. С учетом этого уравнение (1) может быть переписано иначе (3) Аналогично могут быть записаны дифференциальные уравнения
- 12. Вынеся за скобки Y(р) слева и Х(р) справа и разделив Y(р) на Х(р) получим: (5) Отношение
- 13. 3. Временные характеристики. Временной характеристикой называется зависимость изменения выходной величины от входной во времени y(t) =
- 14. 4. Частотные характеристики. Определяются путем приложения к входу звена возмущающего воздействия синусоидальной формы, например, перемещением регулирующего
- 15. При установившихся колебаниях x, если звено или объект являются линейными, сигнал на его выходе также изменяется
- 16. 2. Формы математического описания. 2) в тригонометрической форме: 3) в алгебраической форме: и Вернемся к понятию
- 17. Используя показательную форму, получим: - амплитудно-фазо- частотная характеристика (АФЧХ), где - амплитудно- частотная характеристика (АЧХ) АЧХ
- 18. Значение частотной функции можно представить в виде вектора на комплексной плоскости. При этом каждой частоте будет
- 19. Вопросы для самопроверки: 1) Назовите формы математического описания. 2) Что такое линеаризация? 3) В чем смысл
- 20. Проверим себя ? 1. Операция замены нелинейных уравнений системы приближенными линейными уравнениями называется … А) линеаризацией;
- 22. Скачать презентацию



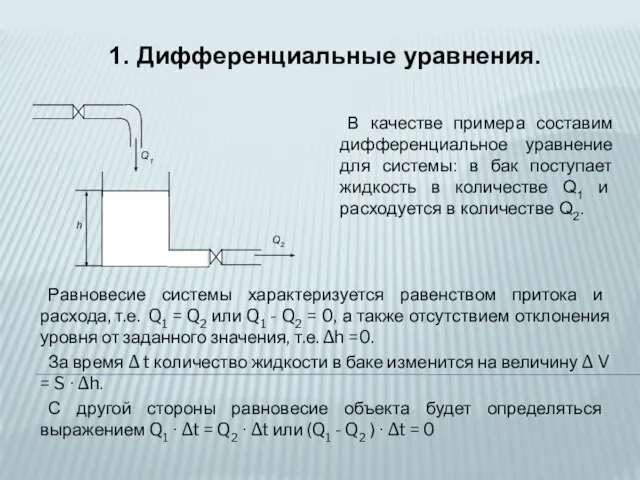















 Таблица умножения числа 2 и на 2
Таблица умножения числа 2 и на 2 Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1
Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1 Статистический анализ результатов мониторинга
Статистический анализ результатов мониторинга Вынесение общего множителя за скобки. 6 класс
Вынесение общего множителя за скобки. 6 класс Степень с натуральным показателем. Задания
Степень с натуральным показателем. Задания Решение уравнений. Элективный курс. Алгебра 11 класс. Урок 2
Решение уравнений. Элективный курс. Алгебра 11 класс. Урок 2 Принадлежность точки выделенной области. 10 класс
Принадлежность точки выделенной области. 10 класс Уравнения, системы уравнений. Задание №9
Уравнения, системы уравнений. Задание №9 Теория расписаний. Минимизация приоритето-порождающих функций
Теория расписаний. Минимизация приоритето-порождающих функций Математическое описание случайных явлений
Математическое описание случайных явлений Операции над множествами
Операции над множествами Презентация на тему Занимательная математика (5 класс)
Презентация на тему Занимательная математика (5 класс)  Учимся считать. Интерактивный тренажёр
Учимся считать. Интерактивный тренажёр Упрощение выражений
Упрощение выражений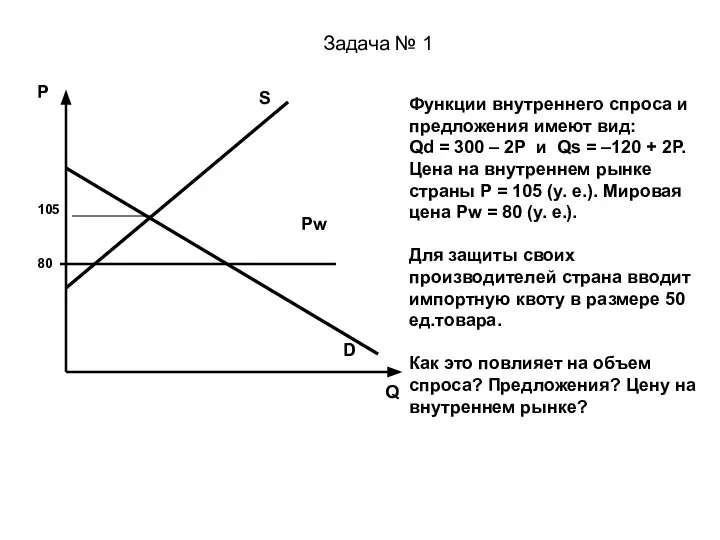 Функции внутреннего спроса и предложения. Разбор задач
Функции внутреннего спроса и предложения. Разбор задач Презентация на тему Свойства логарифмов (10 класс)
Презентация на тему Свойства логарифмов (10 класс)  Математика в профессии сварщика
Математика в профессии сварщика Задачи на перебор вариантов
Задачи на перебор вариантов Прикладной количественный анализ заголовков
Прикладной количественный анализ заголовков Путешествие в историю математики. Решение старинных задач
Путешествие в историю математики. Решение старинных задач Прямоугольные треугольники
Прямоугольные треугольники История развития экономико-математических методов (ЭММ) и моделей. Лекция 1
История развития экономико-математических методов (ЭММ) и моделей. Лекция 1 Презентацию подготовила Кулагина В.В. Учитель начальных классов ФКОУ СОШ имени А.Н.Радищева Г. Кузнецк-12 2012г.
Презентацию подготовила Кулагина В.В. Учитель начальных классов ФКОУ СОШ имени А.Н.Радищева Г. Кузнецк-12 2012г. Округление десятичных дробей. Опорные конспекты
Округление десятичных дробей. Опорные конспекты Подборка заданий по геометрии за курс 7 класса
Подборка заданий по геометрии за курс 7 класса Задачи с цифрами 1, 5, 9
Задачи с цифрами 1, 5, 9 Математика в медицине
Математика в медицине Векторное произведение векторов
Векторное произведение векторов