Свойства тригонометрических функций

Проверь себя.

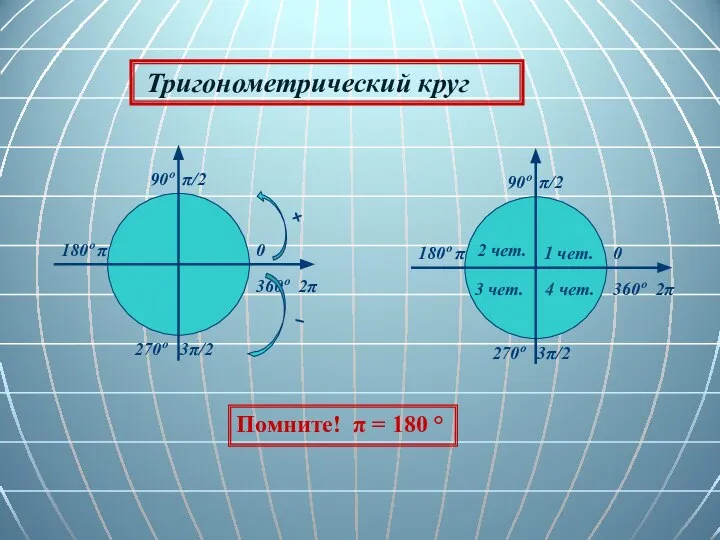
0
90º π/2
180º π
270º 3π/2
360º 2π
Тригонометрический круг
0
90º π/2
180º π
270º 3π/2
360º 2π
1 чет.
2 чет.
3 чет.
4 чет.
Помните! π = 180 °

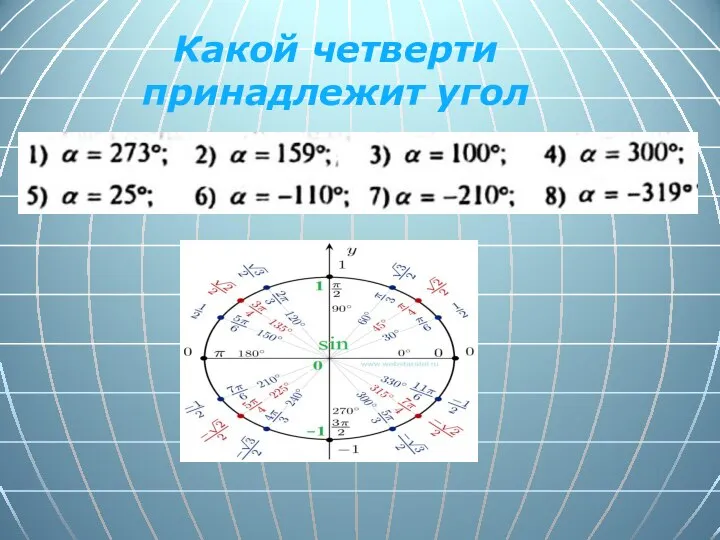
Какой четверти принадлежит угол

Область определения функции
Областью определения функции называют множество всех допустимых значений переменной x. Геометрически – это проекция графика функции на ось Ох.

Область определения
Синус, косинус
D(y) = R
Функции непрерывны на R
Tангенс
D(y) = R, x ≠ π/2 + πn
x = π/2 + πn – вертикальная асимптота
Котангенс
D(y) = R, x ≠ πn
x = πn – вертикальная асимптота
tgx – определен при cosx ≠ 0
ctgx – определен при sinx ≠ 0

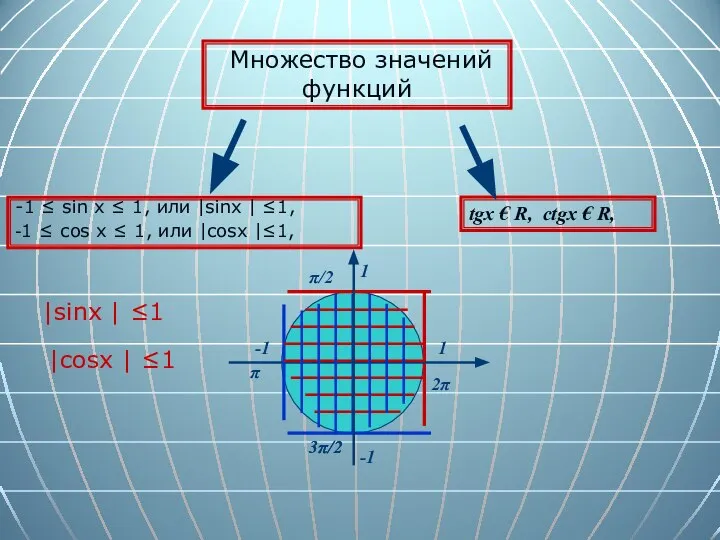
Множество значений функции
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически – это проекция графика функции на ось Оy.

Множество значений функций
tgx € R, ctgx € R,
-1 ≤ sin х ≤ 1, или |sinx | ≤1,
-1 ≤ cos х ≤ 1, или |cosx |≤1,
π
3π/2
2π
3π/2
π/2
1
-1
1
-1
|sinx | ≤1
|cosx | ≤1

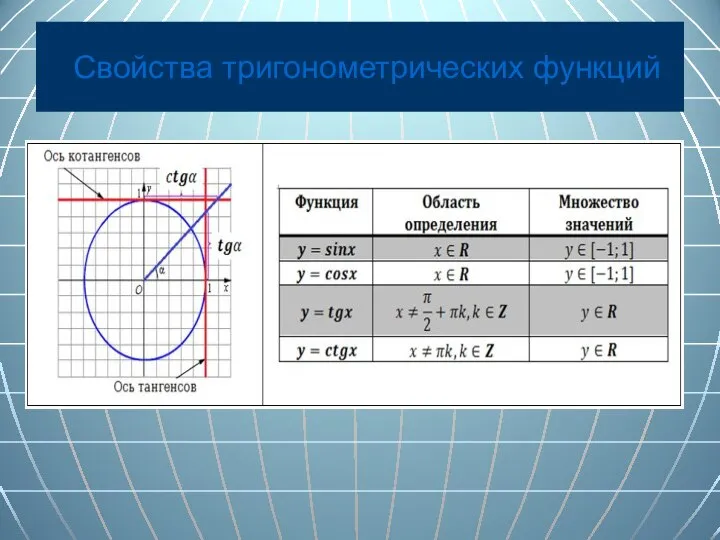
Свойства тригонометрических функций

Найди область определения функции
y = 2sin⁡(x + 3).
Область определения функции – это множество всех значений аргумента, при котором записанная формула функции имеет смысл. Так как sinx имеет смысл при всех значений переменной x, областью определения функции
y = 2sin⁡(x + 3) является вся числовая прямая, т.е. (–∞; +∞).

Найди сумму всех целых значений функции y = – 6 cosx + 1.
Решение. Так как множество значений функции y = cosx – промежуток [–1; 1], тогда:
–1 ≤ cosx ≤ 1,
–6 ≤ –6cosx ≤ 6,
–5 ≤ –6cosx + 1 ≤ 7,
т.е. множество значений функции y = –6cosx + 1 – промежуток [–5; 7]. Этому промежутку принадлежат следующие целые числа:
–5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, 6, 7.
Найди сумму этих чисел:
(–5) + (–4) + (–3) + (–2) + (–1) + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 = 13.
Ответ: 13.

Найди область значений функции ⁡y⁡ = 2cos⁡x.
Так как множество значений функции y = cosx – промежуток [–1; 1], тогда:
–1 ≤ cosx ≤ 1,
–2 ≤ 2cosx ≤ 2,
т.е. множество значений функции
y = 2cosx – промежуток [–2; 2].

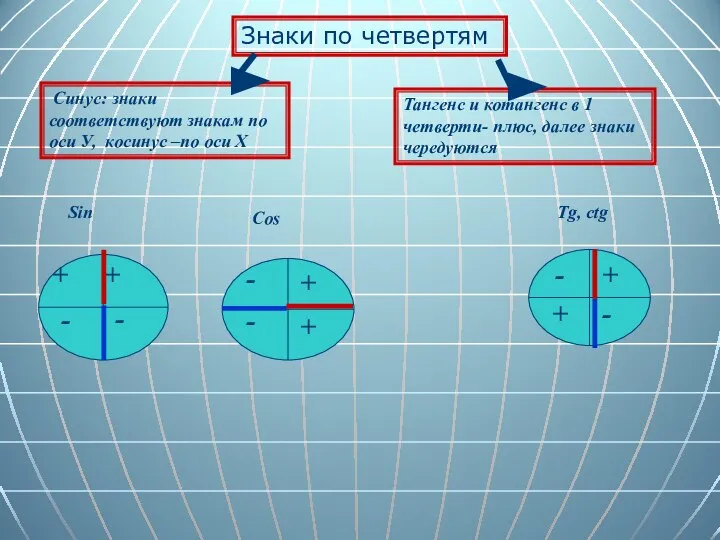
Знаки по четвертям
Синус: знаки соответствуют знакам по оси У, косинус –по оси Х
Тангенс и котангенс в 1 четверти- плюс, далее знаки чередуются

Рассмотрим примеры

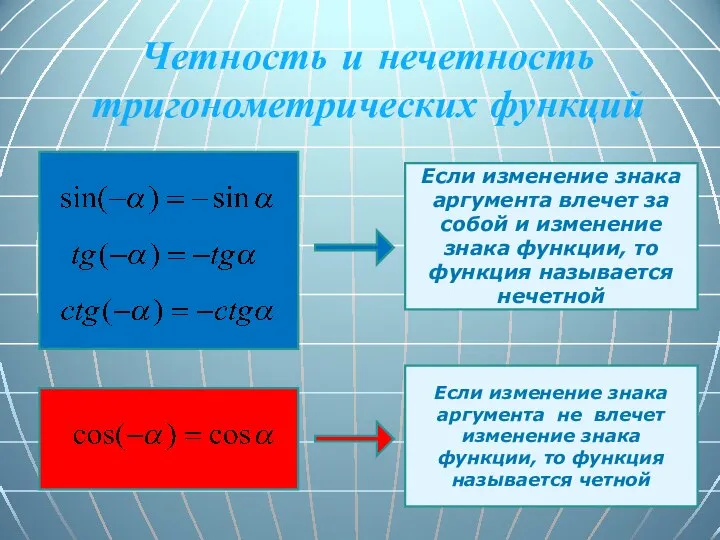
Четность и нечетность тригонометрических функций
Если изменение знака аргумента влечет за собой и изменение знака функции, то функция называется нечетной
Если изменение знака аргумента не влечет изменение знака функции, то функция называется четной

Четность, нечетность
Синус, тангенс, котангенс –функции
нечетные
Минус у угла можно вынести за знак функции
Примеры
1. sin ( – х) = - sin х
2. sin ( π/4 – х) = - sin ( х - π/4 )
4. cos (-7π/3)= cos 7π/3 = cos (2π + π/3) = cos π/3 = ½
5. cos (-β) = cos β
6. ctg ( 2α - π/2) = - ctg (π/2 - 2α )
Косинус – функция
четная
Минус у угла можно опустить

Рассмотрим примеры
cos (-120°)= cos 120°
sin (-120°)=- sin 120°
tg (-45°)=-tg 45°
сtg (-60°)=-сtg 60°

Период
Период – это число, при прибавлении которого к аргументу значение функции не изменяется.
f(x +Т) =f(x)
Если Т – период, то Tn для n € Z тоже период.
Считается Т – наименьший период
Так как f(x +Тn) = f(x), то Tn можно опустить
sin, cos Т=2π
tg, ctg Т=π

Рассмотрим примеры
Найдем
1)
2)
3)