Содержание
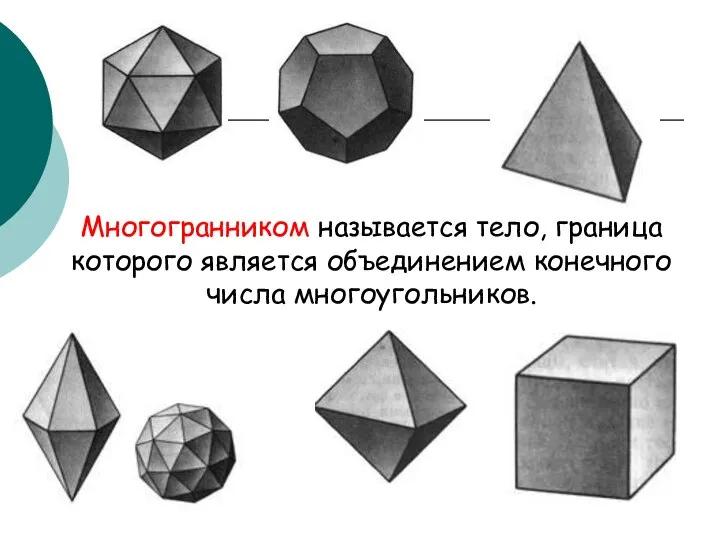
- 2. Многогранником называется тело, граница которого является объединением конечного числа многоугольников.
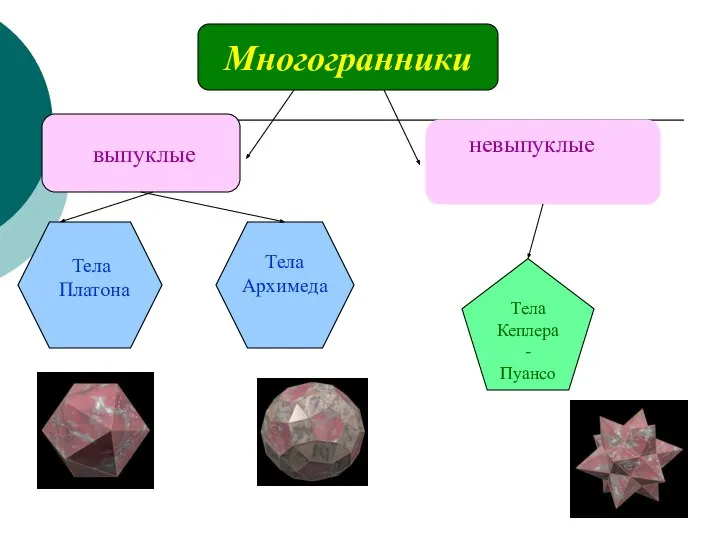
- 3. Многогранники выпуклые невыпуклые Тела Архимеда Тела Платона Тела Кеплера- Пуансо
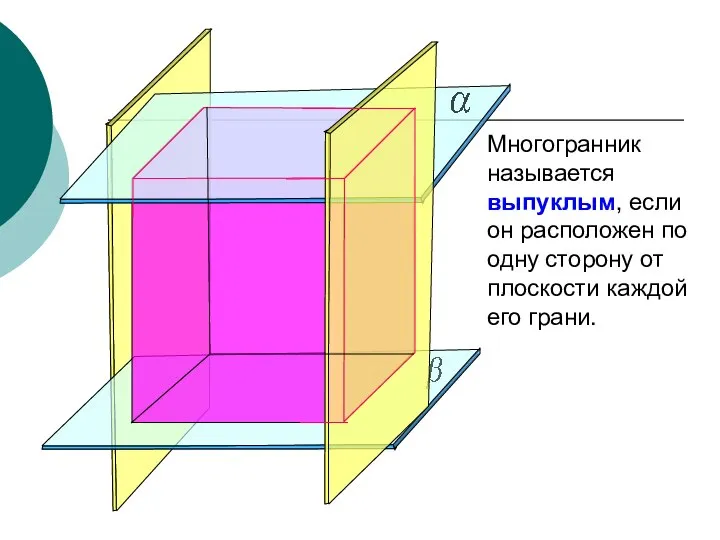
- 4. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
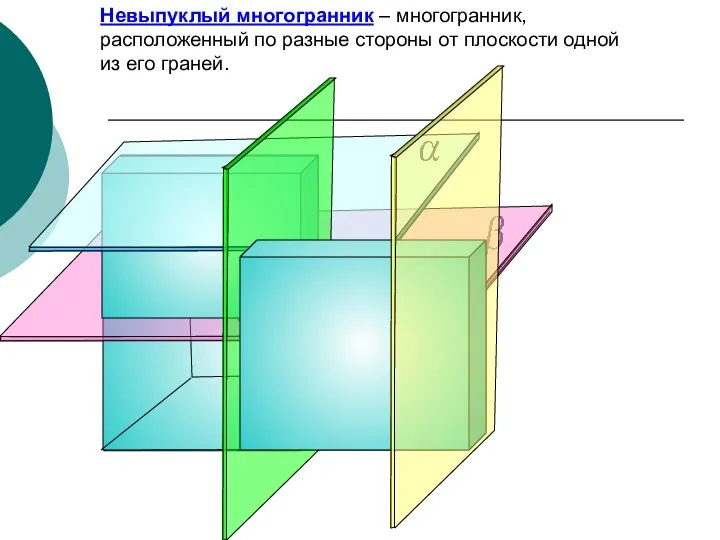
- 5. Невыпуклый многогранник – многогранник, расположенный по разные стороны от плоскости одной из его граней.
- 6. Правильными многогранниками называют выпуклые многогранники, все грани и все углы которых равны, причем грани - правильные
- 7. Правильные многогранники Сколько же их существует?
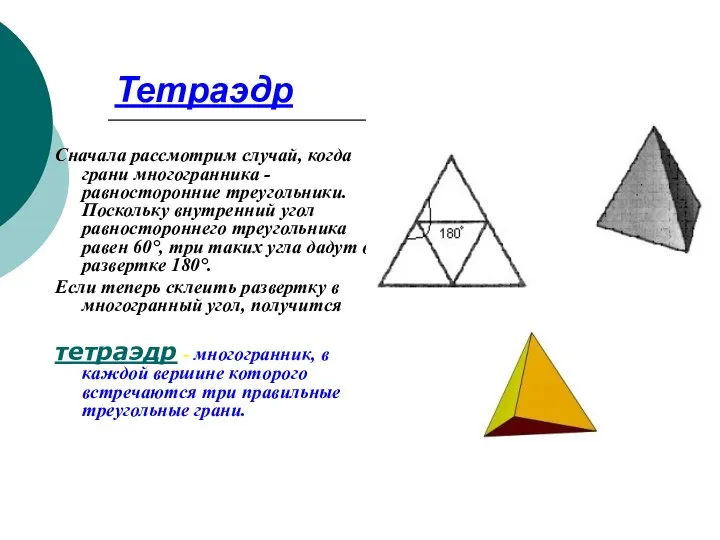
- 8. Тетраэдр Сначала рассмотрим случай, когда грани многогранника - равносторонние треугольники. Поскольку внутренний угол равностороннего треугольника равен
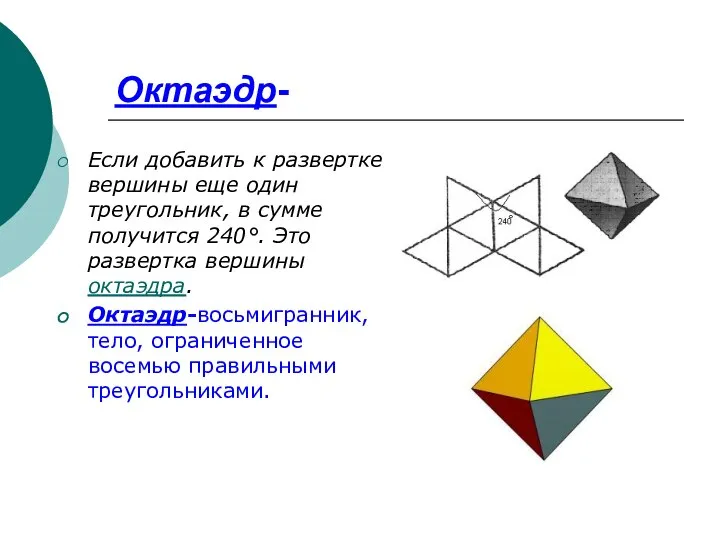
- 9. Октаэдр- Если добавить к развертке вершины еще один треугольник, в сумме получится 240°. Это развертка вершины
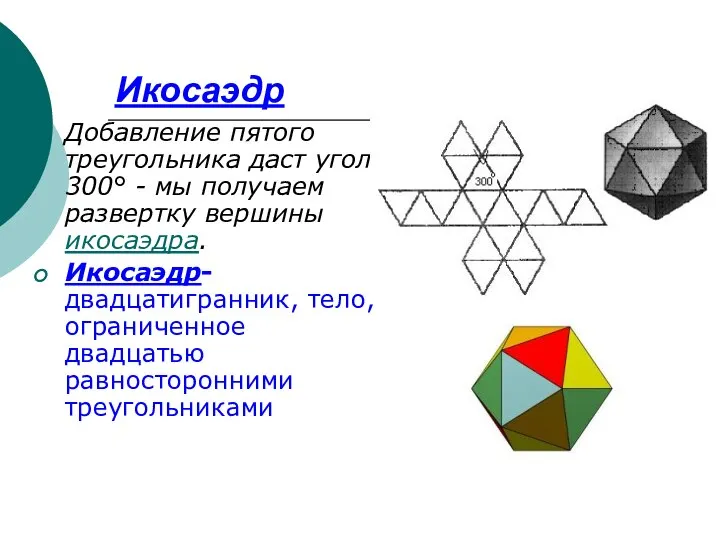
- 10. Икосаэдр Добавление пятого треугольника даст угол 300° - мы получаем развертку вершины икосаэдра. Икосаэдр-двадцатигранник, тело, ограниченное
- 11. Если же добавить еще один, шестой треугольник, сумма углов станет равной 360° - эта развертка, очевидно,
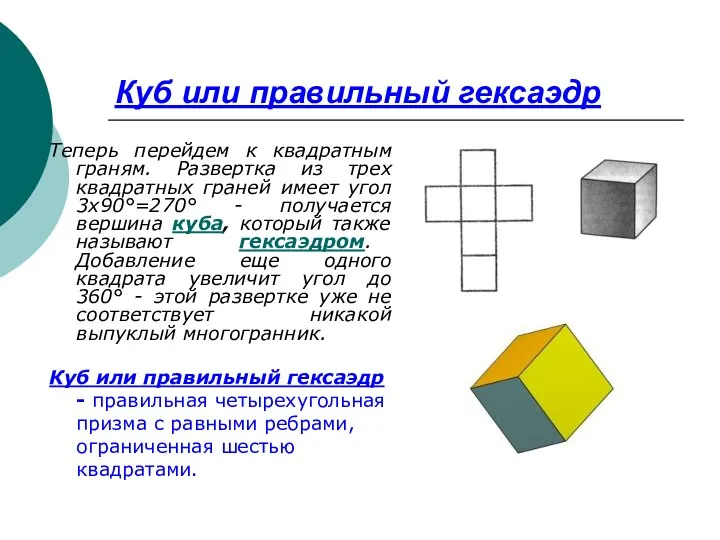
- 12. Куб или правильный гексаэдр Теперь перейдем к квадратным граням. Развертка из трех квадратных граней имеет угол
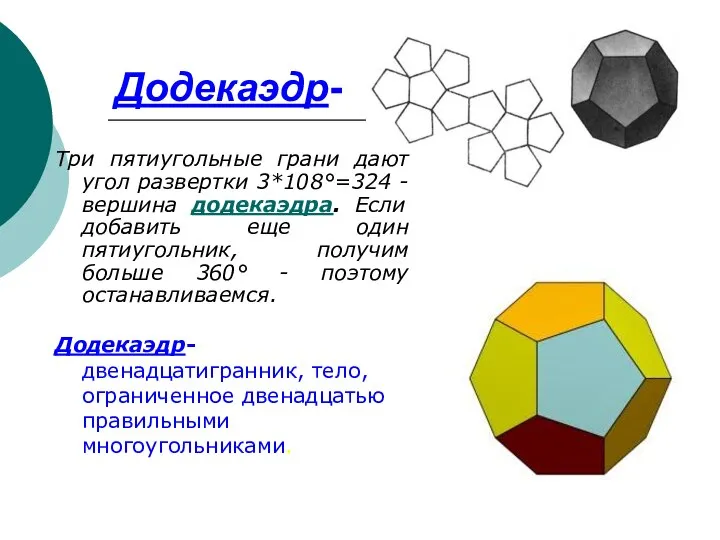
- 13. Додекаэдр- Три пятиугольные грани дают угол развертки 3*108°=324 - вершина додекаэдра. Если добавить еще один пятиугольник,
- 14. Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями
- 15. Сделаем вывод: Мы убедились, что существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр
- 16. Тетраэдр Икосаэдр Гексаэдр Додекаэдр Октаэдр
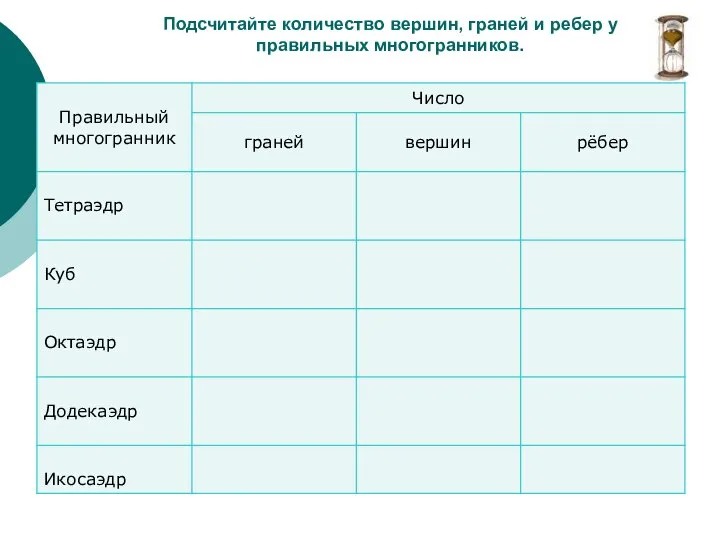
- 17. Подсчитайте количество вершин, граней и ребер у правильных многогранников.
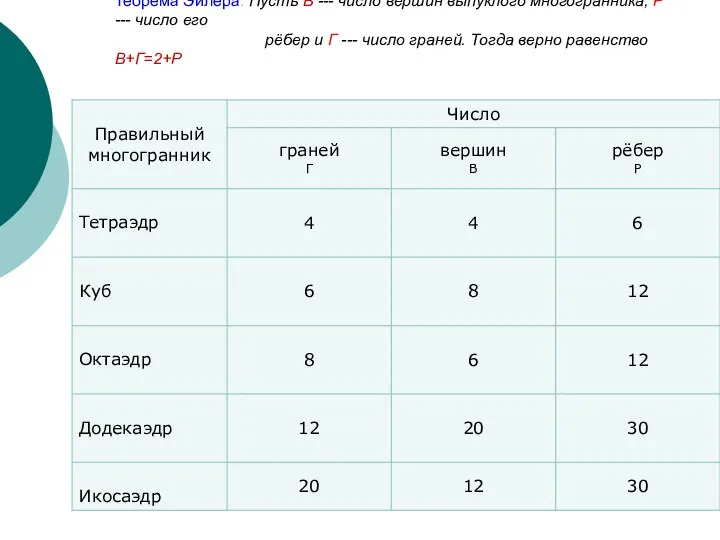
- 18. Теорема Эйлера. Пусть В --- число вершин выпуклого многогранника, Р --- число его рёбер и Г
- 19. История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней
- 20. Эти тела еще называют телами Платона Платон связал с этими телами формы атомов основных стихий природы.
- 21. огонь тетраэдр вода икосаэдр воздух октаэдр земля гексаэдр вселенная додекаэдр стихии
- 22. Все использовали в своих философских теориях правильные многогранники. Дальнейшее развитие математики связано с именами Платона, Евклида,
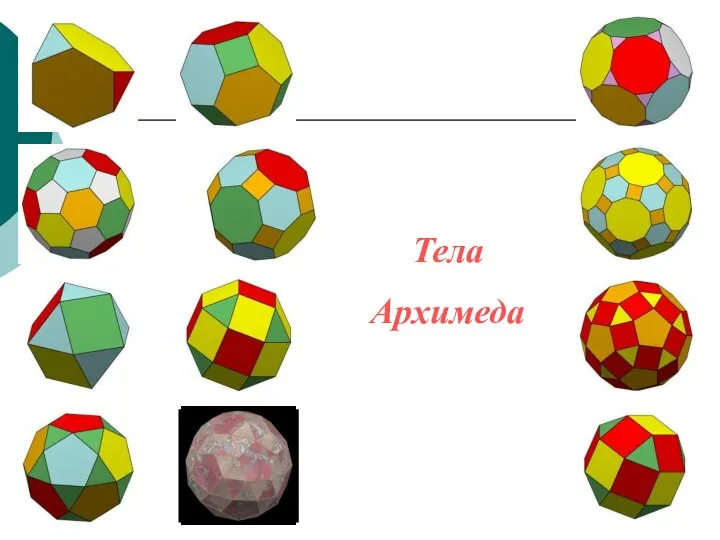
- 23. Тела Архимеда Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники, все многогранные углы
- 24. Тела Архимеда
- 25. Тела Кеплера - Пуансо Среди невыпуклых однородных многогранниковСреди невыпуклых однородных многогранников существуют аналоги платоновых тел -
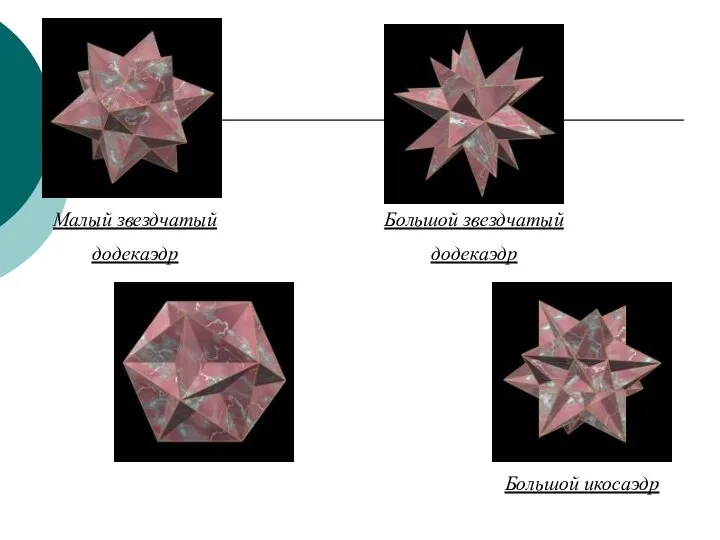
- 26. Большой звездчатый додекаэдр Большой икосаэдр Малый звездчатый додекаэдр
- 27. Многогранники в архитектуре Великая пирамида в Гизе. Эта грандиозная Египетская пирамида является древнейшим из Семи чудес
- 29. Многогранники в архитектуре Москвы Собор непорочного зачатия Девы Марии на малой Грузинской Исторический музей
- 30. Малый Ржевский пер. Новоарбатский замок Многогранники в архитектуре Москвы
- 31. Казанская церковь в Москве Многогранники в архитектуре Москвы
- 32. Чудо природы – кристаллы куб передает форму кристаллов поваренной соли NaCl монокристалл алюминиево-калиевых квасцов имеет форму
- 33. Многогранники в природе Правильные многогранники – самые выгодные фигуры. И природа этим широко пользуется. Подтверждением тому
- 34. Пчёлы строили свои шестиугольные соты задолго до появления человека.
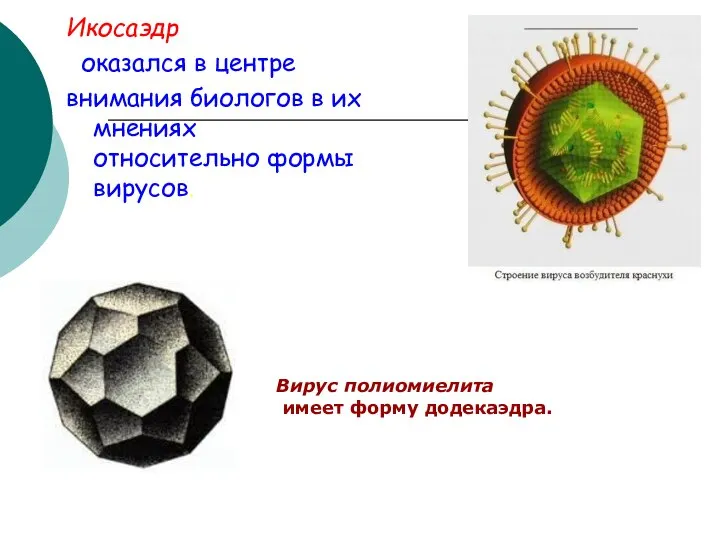
- 35. Икосаэдр оказался в центре внимания биологов в их мнениях относительно формы вирусов. Вирус полиомиелита имеет форму
- 36. Многогранники в химии
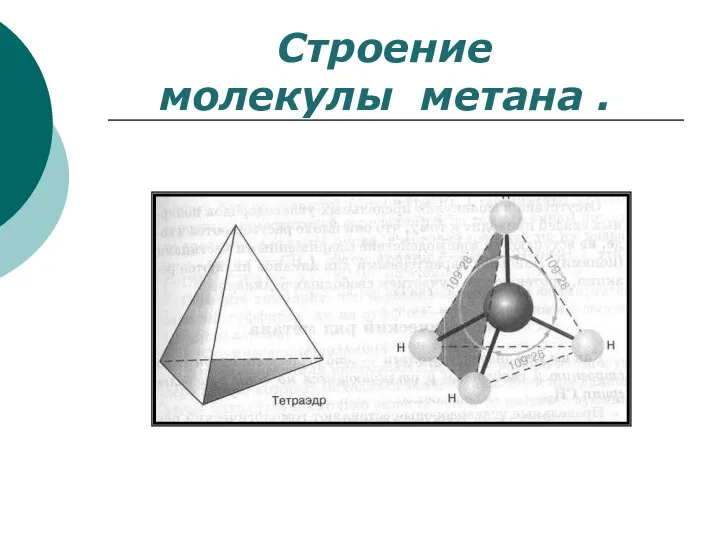
- 37. Строение молекулы метана .
- 38. Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии по форме напоминает икосаэдр.
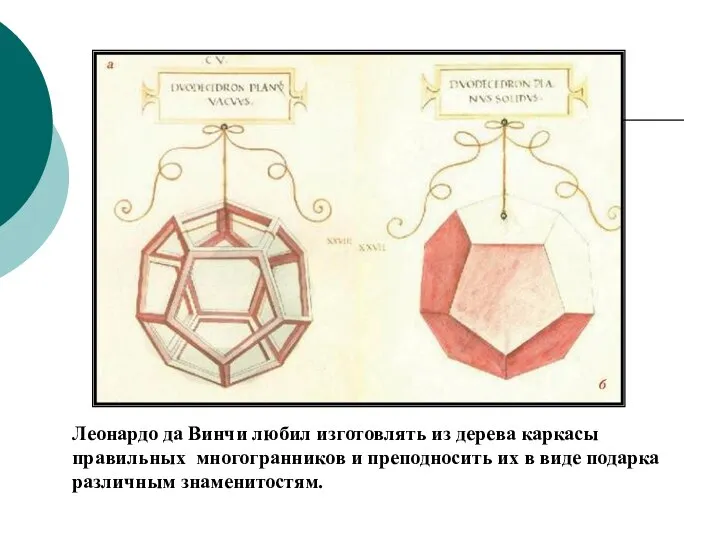
- 39. Леонардо да Винчи любил изготовлять из дерева каркасы правильных многогранников и преподносить их в виде подарка
- 40. Правильная форма алмаза.
- 41. Тестирование. А теперь проверьте свои знания по изученному материалу
- 42. 1. Поверхность, составленная из четырех треугольников А) ТЕТРАЭДР С) КВАДРАТ B) ПАРАЛЛЕЛЕПИПЕД D) ШАР
- 43. 2. Поверхность, составленная из многоугольников и ограничива- ющая некоторое геометрическое тело А) МНОГОУГОЛЬНИК С) ТРЕУГОЛЬНИК B)
- 44. 3. Многоугольник, из которого составлен многогранник А) СТОРОНА С) ГРАНЬ B) РЕБРО D) ВЕРШИНА
- 45. 4. Отрезок, соединяющий две вершины, не принадлежащие одной грани А) ДИАГОНАЛЬ С) ВЫСОТА B) МЕДИАНА D)
- 46. 5. Высота боковой грани правильной пирамиды, проведенная из ее вершины А) ДИАГОНАЛЬ С) КАТЕТ B) АПОФЕМА
- 47. 6. Этот правильный многогранник составлен из 8-ми равносторонних треугольников А) КВАДРАТ С) ДОДЕКАЭДР B) ТЕТРАЭДР D)
- 48. 7. Составлен из 6-ти правильных четырехугольников А) КВАДРАТ С) КУБ B) ТЕТРАЭДР D) ПИРАМИДА
- 49. 8. Стихия тетраэдра А) ВОДА С) ЗЕМЛЯ B) ВОЗДУХ D) ОГОНЬ
- 50. 9. Многоугольник, подобный пчелиным сотам А) 8-МИ УГОЛЬНИК С) 4-Х УГОЛЬНИК B) 6-ТИ УГОЛЬНИК D) ТРЕУГОЛЬНИК
- 51. Проверь себя. 1. A 2. B 3. C 4. A 5. B 6. D 7. C
- 53. Скачать презентацию


























 Математика в профессии сварщика
Математика в профессии сварщика Теория вероятностей. Действия над вероятностями
Теория вероятностей. Действия над вероятностями Числовые и буквенные выражения
Числовые и буквенные выражения ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА Измерение объема жидких и сыпучих веществ с помощью условной меры масс
Измерение объема жидких и сыпучих веществ с помощью условной меры масс Интерактивный пазл
Интерактивный пазл Среднее арифметическое
Среднее арифметическое Производная сложной функции
Производная сложной функции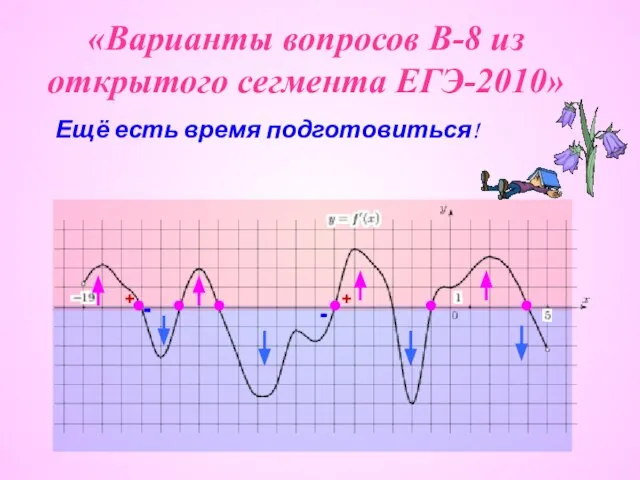 Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Построение графиков функций при помощи геометрических преобразований
Построение графиков функций при помощи геометрических преобразований Математика в лицах.11б
Математика в лицах.11б Теория вероятностей
Теория вероятностей Стандартный вид одночлена
Стандартный вид одночлена Когда выполнение одного условия обеспечивает выполнение другого
Когда выполнение одного условия обеспечивает выполнение другого Виды неопределенностей и методы их разрешения
Виды неопределенностей и методы их разрешения Тренажёр. Таблица умножения. Юные водители
Тренажёр. Таблица умножения. Юные водители Частные производные второго порядка. Первый и второй дифференциалы. Локальный экстремум
Частные производные второго порядка. Первый и второй дифференциалы. Локальный экстремум Математика. Составные высказывания
Математика. Составные высказывания Математика. 3 класс
Математика. 3 класс Справедливость равенства. Устный счет
Справедливость равенства. Устный счет Понятие десятичной дроби
Понятие десятичной дроби Разложение вектора по трем некомпланарным векторам
Разложение вектора по трем некомпланарным векторам Весёлая математика. А ну-ка посчитай
Весёлая математика. А ну-ка посчитай Векторный анализ -теория поля. Типы векторных полей. Лекция 18
Векторный анализ -теория поля. Типы векторных полей. Лекция 18 Математический анализ. Исследование функций и построение графиков. Асимптоты графика функции
Математический анализ. Исследование функций и построение графиков. Асимптоты графика функции Кривая Коха. Дробная размерность. Метод L-систем
Кривая Коха. Дробная размерность. Метод L-систем Показательное уравнение
Показательное уравнение Пифагор и его теорема
Пифагор и его теорема