Разбор и решение задания ОГЭ по математике

Цель работы:
Научиться решать задание из ОГЭ модуля «Геометрия»
Подкорректировать усвоенные знания, умения и навыки.

Так как задания основаны на теории по теме "треугольники", рассмотрим базовые понятия, определения и формулы.
Вначале предлагаю рассмотреть углы на плоскости:
Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой.
Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
Внутренние односторонние углы - это углы, которые лежат внутри между прямыми по одну сторону от секущей.

Многие задачи построены на нахождении медиан и биссектрис треугольника:
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.

Медиана:

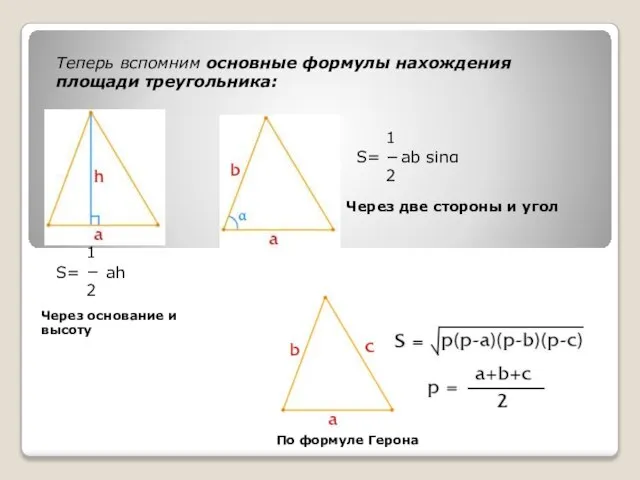
Теперь вспомним основные формулы нахождения площади треугольника:
1
−
2
ah
S=
S=
1
−
2
ab sinα
Через основание и высоту
Через две стороны и угол
По формуле Герона

Во многих задачах встречается понятие средняя линия:
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
Средняя линия параллельна третьей стороне и равна её половине.
Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.

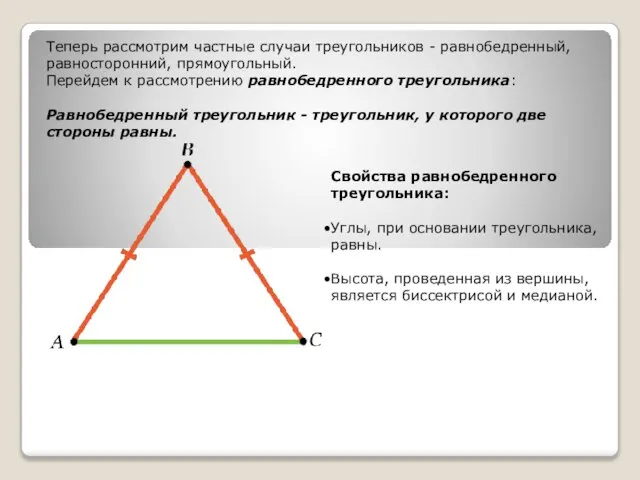
Теперь рассмотрим частные случаи треугольников - равнобедренный, равносторонний, прямоугольный.
Перейдем к рассмотрению равнобедренного треугольника:
Равнобедренный треугольник - треугольник, у которого две стороны равны.
Свойства равнобедренного треугольника:
Углы, при основании треугольника, равны.
Высота, проведенная из вершины, является биссектрисой и медианой.

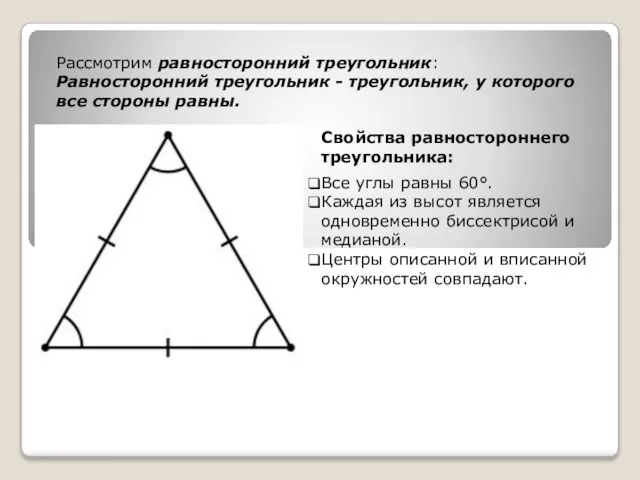
Рассмотрим равносторонний треугольник:
Равносторонний треугольник - треугольник, у которого все стороны равны.
Все углы равны 60°.
Каждая из высот является одновременно биссектрисой и медианой.
Центры описанной и вписанной окружностей совпадают.
Свойства равностороннего треугольника:

Прямоугольный треугольник
Треугольник называется прямоугольным, если один из его углов прямой.
Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой.
Для прямоугольного треугольника справедливы следующие утверждения:
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
Сумма острых углов треугольника равна 90°:
Катет, лежащий против угла, равен половине гипотенузы.
Две высоты прямоугольного треугольника совпадают с его катетами.
Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.
Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

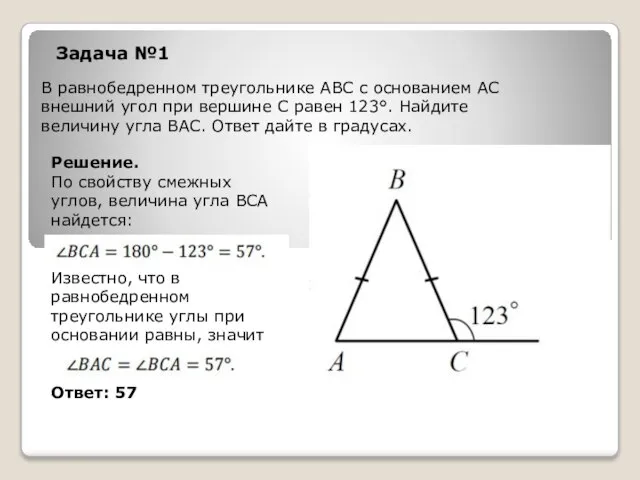
В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине С равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах.
Задача №1
Решение.
По свойству смежных углов, величина угла ВСА найдется:
Известно, что в равнобедренном треугольнике углы при основании равны, значит
Ответ: 57

Задача №2
В треугольнике ABC известно, что АВ=ВС. Угол АВС=102°. Найдите угол ВСА. Ответ дайте в градусах.
Решение.
Треугольник АВС – равнобедренный, Следовательно,
Ответ: 39

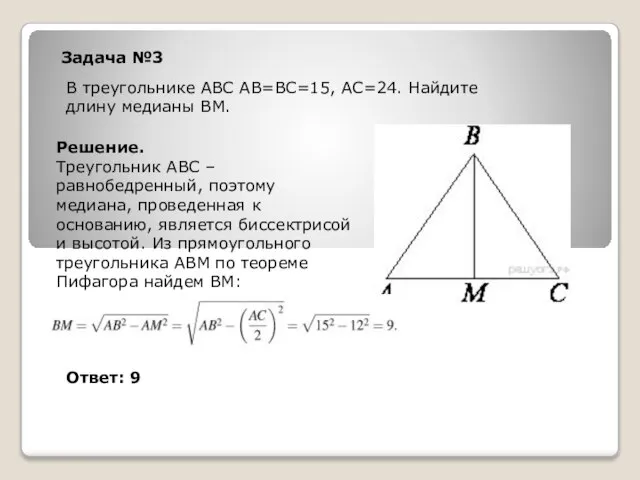
Задача №3
В треугольнике ABC АВ=ВС=15, АС=24. Найдите длину медианы ВМ.
Решение.
Треугольник АВС – равнобедренный, поэтому медиана, проведенная к основанию, является биссектрисой и высотой. Из прямоугольного треугольника АВМ по теореме Пифагора найдем ВМ:
Ответ: 9

Задача №4
Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.
Решение
Формула площади для прямоугольного треугольника выглядит следующим образом:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Это следует из того, что один из катетов является высотой к основанию, которым является второй катет. Следовательно,
S = ½ • 15 • 4 = 30
Ответ:30