Множества

Все ученики класса
Все делители числа 6: 1; 2; 3;6
Все точки плоскости,
удалённые от точки О на 2см
Всё это наборы объектов, объединённых общим для каждого набора свойством..

Наборы объектов, объединённых общим для каждого набора свойством называют множествами
«Множество учеников класса»
«Множество делителей числа 6»
«Множество точек плоскости,
удалённых от точки О на 2см»

В математике термин «множество» не имеет количественного смысла.
Множество делителей числа 1 состоит из одного элемента – числа 1 – это множество конечное.
Множество общих кратных чисел 2 и 3 является бесконечным – 6, 12, 18, 24, ….

В математике встречаются множества, в которых нет ни одного элемента, например множество чисел, делящихся на нуль. Такое множество называют пустым.
Ø – пустое множество

Числа 1, 2, 3, 4, 6, 12 – являются элементами множества делителей числа 12
«1, 2, 3, 4, 6, 12 – принадлежат (∈) множеству делителей числа 12»
«5, 7 – не принадлежат(∉) множеству делителей числа 12»

Великий математик XVIIIв. Леонард Эйлер предложил изображать множества кругами, а элементы множеств – точками внутри этих кругов.

А – множество делителей числа 12 (1, 2, 3 ,4, 6, 12)
В – множество делителей числа 18 (1, 2, 3 , 6, 9, 18)
Множество элементов, общих для множеств А и В, называют пересечением множеств А и В.

К поиску пересечения множеств сводится решение некоторых геометрических задач.
ЗАДАЧА: Построить треугольник АВС со сторонами АВ=2,5 см, ВС=3 см и АС=2см.

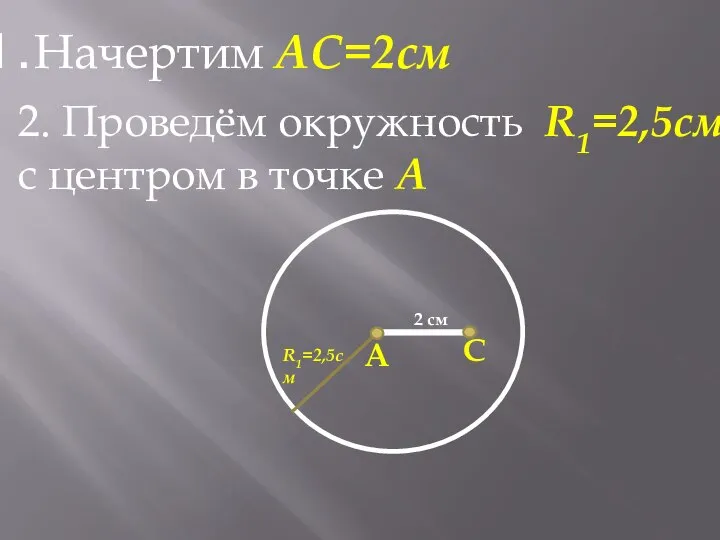
Начертим АС=2см
А
С
2 см
2. Проведём окружность R1=2,5см c центром в точке А
R1=2,5см

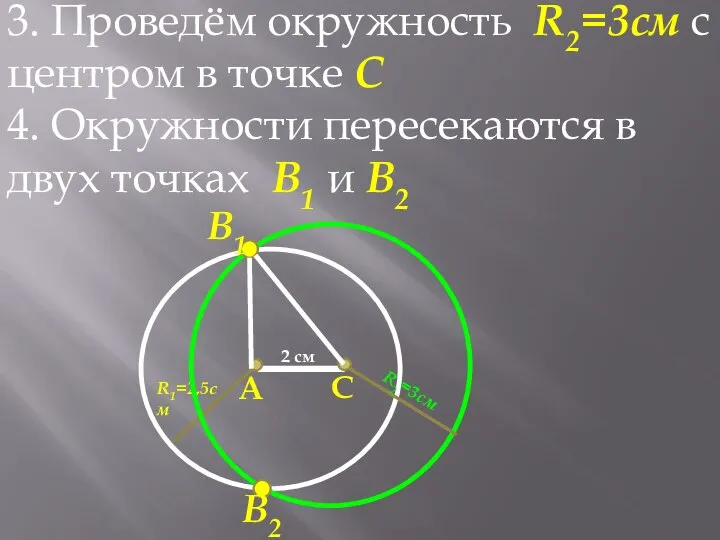
А
С
2 см
3. Проведём окружность R2=3см c центром в точке С
R1=2,5см
R2=3см
4. Окружности пересекаются в двух точках В1 и В2
В1
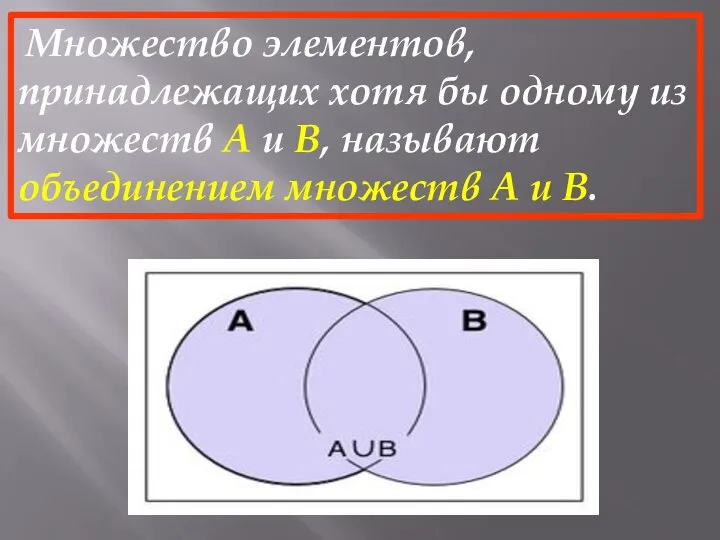
В2

Множество элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением множеств А и В.

А – множество делителей числа 12 (1, 2, 3 ,4, 6, 12)
В – множество делителей числа 18 (1, 2, 3 , 6, 9, 18)

Множество А называют подмножеством множества В, если каждый элемент множества А принадлежит множеству В
B
A
A ⊂ B

B – множество делителей числа 12 (1, 2, 3 ,4, 6, 12)
A – множество делителей числа 6 (1, 2, 3 , 6)
A ⊂ B

Два множества равны, если они состоят из одних и тех же элементов или вообще не содержат элементов.