Слайд 2Задача Мише учитель математики поставил в дневник отметку «2». Миша, желая скрыть

от мамы данный факт, порвал свой дневник на 4 части. Этого ему показалось мало, поэтому некоторые из этих частей (может быть и не все) он порвал на 4 части и так далее. Мама нашла 20 «кусочков» дневника. Все ли куски нашла мама?
Слайд 3Решение:
Для того, чтобы решить задачу, необходимо ответить на вопрос: «Какое число обрывков

могло получиться?» Сначала Миша порвал дневник на 4 части. Если он порвал на 4 части один из четырех кусочков, то их станет 4+ 3 = 7. Если Миша и дальше будет рвать кусочки на 4 части, то их будет получаться 4 +6 = 10, 4 + 9 = 13, 4 + 12 = 16, 4 + 15 =19, 4 +18 =22 и так далее. Таким образом, кусочков может быть 4, 7, 10, 13, 16, 19, 22, … Значит, мама нашла не все кусочки. Можно заметить, что при делении каждого из этих чисел на 3 получается остаток 1.
В данной задаче в качестве инварианта выступил остаток от деления на 3.
Слайд 4Задача . Хулиганы Вася и Петя порвали школьную стенгазету, в которой была

заметка об их плохой учебе. Причем Вася рвал каждый кусок на 5 частей, а Петя на 9. Заместитель директора школы, заметив такое безобразие, потребовала собрать обрывки стенгазеты. Ребята нашли 1999 обрывков. Все ли обрывки были найдены и почему?
Слайд 5Решение:
Рассмотрим, какое число обрывков могло получиться. Если Вася первоначально порвал стенгазету на

5 кусков, а затем один из кусков снова на 5, то всего их получается 9. Если теперь Вася будет дальше рвать некоторые куски на 5, а Петя на 9, то число кусков может получиться 5, 9, 13, 17, 21 и т. д. Можно заметить, что общее число кусков можно записать как 4n+1. Так как 1999=499×4+3, то ученики собрали не все обрывки стенгазеты.
В данной задаче в качестве инварианта выступил остаток от деления на 4.
Слайд 6Инвариант – знак произведения.
Сформулируем наиболее важное утверждение, которое используется при решении задач,

где в качестве инварианта выступает знак произведения:
Знак произведения нескольких (отличных от нуля) чисел определяется четностью количества отрицательных множителей.
Слайд 7Приведем примеры:
1. Число (-1) × (-2) × (-3) × (-4) положительно, так

как в произведении четное число отрицательных множителей.
2. Число (-1) × 2 × (-3) × 4 × (-5) отрицательно, так как в произведении нечетное число отрицательных множителей.
Применяя это утверждение, решим следующие задачи.
Слайд 8 Задача . Квадрат 5×5 заполнен числами так, что произведение чисел в каждой

строке отрицательно. Доказать, что найдется столбец, в котором произведение чисел так же отрицательно.
Слайд 9Решение:
Найдем произведение всех чисел в квадрате. Так как произведение чисел в каждой

строке отрицательно, то и произведение всех чисел будет отрицательно. Но с другой стороны, произведение всех чисел равно и произведению чисел в столбцах. А так как произведение всех чисел отрицательно, то найдется столбец, в котором произведение чисел является отрицательным.
Инвариантом в этой задаче является знак произведения всех чисел в квадрате – оно отрицательное.
Слайд 10Задача. В каждую клетку квадратной таблицы размером 25×25 вписано произвольно одно из

чисел: +1 или -1. Под каждым из столбцов записывается произведение всех чисел данного столбца, а справа от каждой строки – произведение всех чисел данной строки. Может ли сумма всех 50 произведений быть равной нулю?
Слайд 11Решение:
Перемножая все 50 произведений, мы получим 1, так как в каждое произведение

любое из чисел, вписанных в клетки таблицы, войдет 2 раза - один раз в произведение по строкам, один раз – по столбцам. Тогда в число пятидесяти множителей будет входить четное число произведений, с «-1». Поэтому сумма четного числа произведений, с «1», и четного числа произведений, с «-1», не может быть равна 0. (Одинакового числа слагаемых не будет, так как 50 : 2 = 25 – число нечетное.)
Инвариантом в этой задаче будет знак произведения 50 множителей.











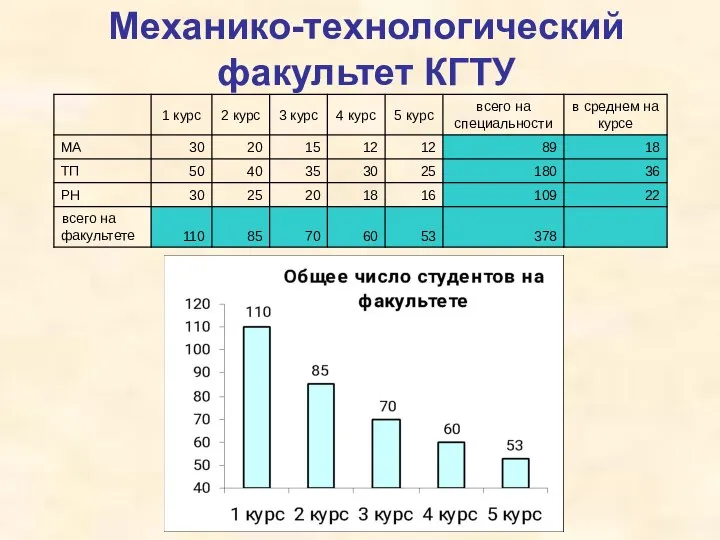 Диаграммы
Диаграммы Առարկա՝ Հյուսվածքները եւ դրանց մոդելները երկրաչափության դպրոցական դասընթացում (ընտրովի դասընթաց)
Առարկա՝ Հյուսվածքները եւ դրանց մոդելները երկրաչափության դպրոցական դասընթացում (ընտրովի դասընթաց) Пирамида. Площади поверхностей. Объём. Многогранники
Пирамида. Площади поверхностей. Объём. Многогранники Системы линейных уравнений СЛУ
Системы линейных уравнений СЛУ Математика. Лекция
Математика. Лекция Действие с дробями. Устная работа
Действие с дробями. Устная работа Степень с натуральным показателем и ее свойства.
Степень с натуральным показателем и ее свойства. Луч. Отрезок
Луч. Отрезок Натуральные числа и дроби. Урок 1
Натуральные числа и дроби. Урок 1 Арифметичская прогрессия
Арифметичская прогрессия Эмпирико-статистические модели климатических изменений. Земля как климатическая система
Эмпирико-статистические модели климатических изменений. Земля как климатическая система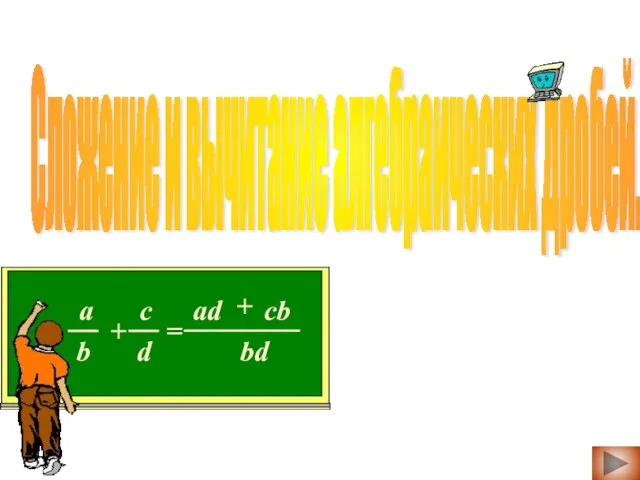 Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Биржа знаний
Биржа знаний Оценка вероятности поражения обслуживающего персонала при подрыве РКН
Оценка вероятности поражения обслуживающего персонала при подрыве РКН Числовые ряды. Признаки сходимости
Числовые ряды. Признаки сходимости Деление одночлена на одночлен
Деление одночлена на одночлен Решение алгебраических и трансцендентных уравнений
Решение алгебраических и трансцендентных уравнений Деление уголком
Деление уголком Уравнение сферы
Уравнение сферы Математическая прогрессия и где её применяют
Математическая прогрессия и где её применяют Письменное умножение чисел, оканчивающихся нулями
Письменное умножение чисел, оканчивающихся нулями Тела вращения. Конус
Тела вращения. Конус Правильные многоугольники в нашей жизни
Правильные многоугольники в нашей жизни Решение систем линейных неравенств с двумя переменными
Решение систем линейных неравенств с двумя переменными Своя игра по геометрии
Своя игра по геометрии Логарифмы
Логарифмы Тригонометрические тождества
Тригонометрические тождества Математический анализ. Исследование функций и построение графиков. Асимптоты графика функции
Математический анализ. Исследование функций и построение графиков. Асимптоты графика функции