Множества и операции над множествами

Понятия теории множеств
Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в математику немецким ученым Георгом Кантором (1845-1918).Следуя Кантору, понятие "множество" можно определить так:
Множество- совокупность объектов, обладающих определенным свойством, объединенных в единое целое.

« Числа в математике»

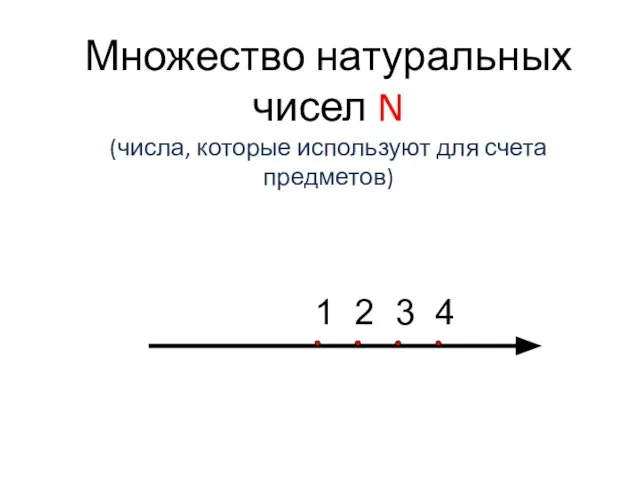
Множество натуральных чисел N
(числа, которые используют для счета предметов)
3
4
1
2

Добавив к ним число 0 и противоположные числа, получили множество
целых чисел Z

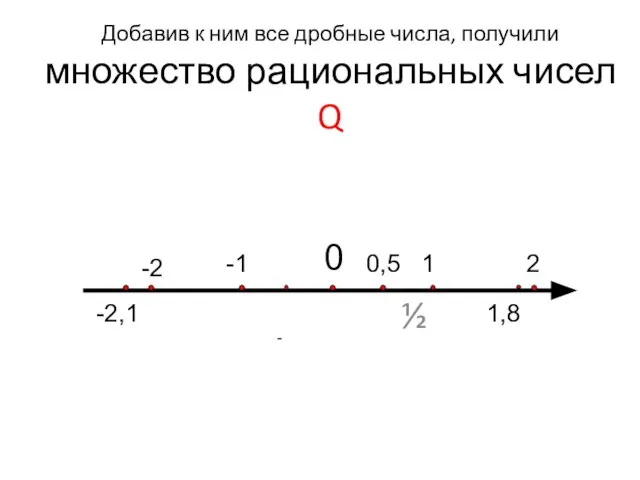
Добавив к ним все дробные числа, получили множество рациональных чисел Q
½
0
1
2
-1
0,5
-2
-2,1
1,8
-

Целые и дробные числа образуют множество рациональных чисел Q
Число, которое можно записать в виде отношения,
где а є Z, а n є N, называют рациональным числом
а/n

1, 414213562373095048… -
бесконечная непериодическая десятичная дробь. Такие числа называются
иррациональными
примеры: π ≈ 3,14

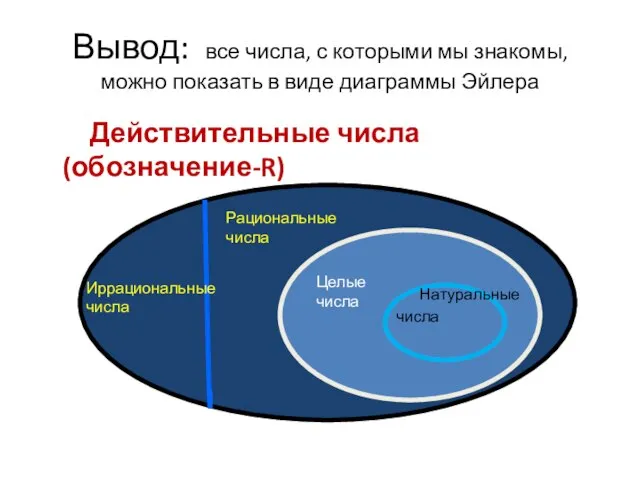
Вывод: все числа, с которыми мы знакомы, можно показать в виде диаграммы Эйлера
Действительные числа (обозначение-R)
Натуральные числа
Целые числа
Рациональные числа
Иррациональные числа

Множество цифр:
0;1;2;3;4;5;6;7;8;9
Множество букв русского алфавита
Например:
1). Цифра 6 – элемент множества цифр.
2). Буква Л – элемент множества букв
русского алфавита
Предметы, из которых состоит множество, называются его ЭЛЕМЕНТАМИ

Для обозначения множеств используют большие
буквы латинского алфавита или фигурные скобки,
внутри которых записывают элементы
множества(при этом порядок элементов не имеет
значения).
Например:
1). А— множество цифр: А={0;1;2;3;4;5;6;7;8;9}.
2). W— множество букв русского алфавита:
W={А;Б;В;Г;Д;Е;Ж;З;И;Й;К;Л;М;Н;О;П;Р;С;Т;У;Ф;Х;Ц;Ч;Ш;Щ; Ь;Ы;Ъ;Э;Ю;Я }

Для обозначения элементов множества используют малые буквы латинского алфавита
Например:
1). f = 6 – элемент множества цифр
2). а = Р – элемент множества букв русского алфавита
Принадлежность предмета данному множеству обозначается
Например:
1). f = 6 ; 6 є А, где А— множество цифр.
2). К є W, где W— множество букв русского алфавита
Непринадлежность – символом

Множество может быть:
1). Конечное :
Например: А— множество цифр
2). Бесконечное:
Например: N – множество натуральных чисел
3). Пустое:
ø- множество, в котором нет ни одного элемента
Например: X – множество решений уравнения

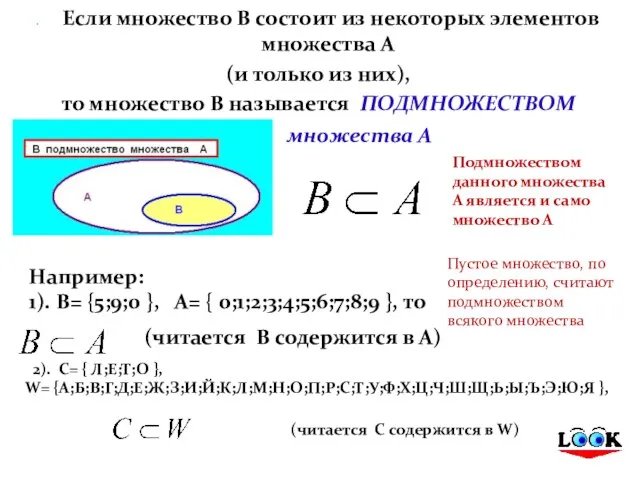
На диаграмме Эйлера-Венна утверждение "множество А является подмножеством множество В" изображают так
Если множество В состоит из некоторых элементов множества А
(и только из них),
то множество В называется ПОДМНОЖЕСТВОМ
множества А
Например:
1). В= {5;9;0 }, А= { 0;1;2;3;4;5;6;7;8;9 }, то
(читается В содержится в А)
2). С= { Л;Е;Т;О },
W= {А;Б;В;Г;Д;Е;Ж;З;И;Й;К;Л;М;Н;О;П;Р;С;Т;У;Ф;Х;Ц;Ч;Ш;Щ;Ь;Ы;Ъ;Э;Ю;Я },
(читается С содержится в W)
Подмножеством данного множества А является и само множество А
Пустое множество, по определению, считают подмножеством всякого множества

Способы задания множеств
Перечислением элементов множества;
Описанием общего (характеристического) свойства, объединяющего элементы.
Например:
1). К = {х : -5 ≤ х ≤ 6 }-описанием характеристического свойства элементов
2). Т = {х : 0 ≤ х ≤ 9, х є N } –описанием характеристического свойства элементов
3). Множество учеников данного класса определяется их списком в классном журнале - перечислением элементов
4). Множество цифр: А = {0,1,2,3,4,5,6,7,8,9} - перечислением элементов

Операции над множествами
Суммой, или объединением произвольного конечного или бесконечного множества множеств называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А,В.
Объединение множеств обозначается
На диаграмме Эйлера-Венна объединение двух множеств выглядит так
П р и м е р : {1,2,3} {2,3,4} = {1,2,3,4}.

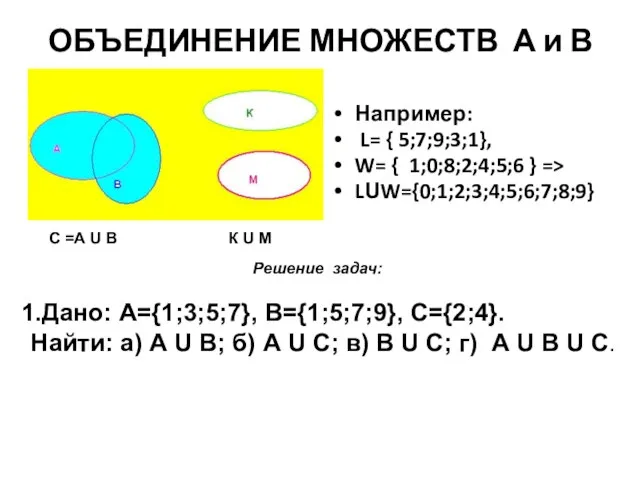
ОБЪЕДИНЕНИЕ МНОЖЕСТВ А и В
Например:
L= { 5;7;9;3;1},
W= { 1;0;8;2;4;5;6 } =>
LUW={0;1;2;3;4;5;6;7;8;9}
С =А U B К U M
Решение задач:
1.Дано: А={1;3;5;7}, В={1;5;7;9}, С={2;4}.
Найти: а) А U В; б) А U С; в) В U С; г) А U В U С.

Пересечением любого конечного или бесконечного множества множеств называется множество, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.
Пересечение множеств обозначается
На диаграмме Эйлера-Венна пересечение двух множеств выглядит так
П р и м е р : {1,2,3} {2,3,4} = {2,3}

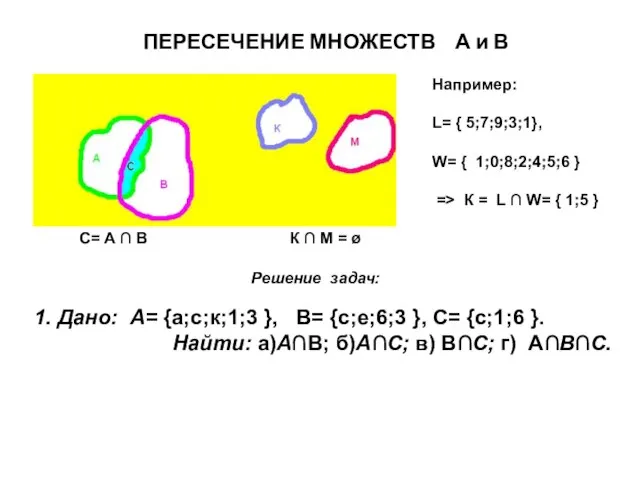
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ А и В
С= А ∩ В К ∩ М = ø
Например:
L= { 5;7;9;3;1},
W= { 1;0;8;2;4;5;6 }
=> К = L ∩ W= { 1;5 }
Решение задач:
1. Дано: А= {а;с;к;1;3 }, В= {с;е;6;3 }, С= {с;1;6 }.
Найти: а)А∩В; б)А∩С; в) В∩С; г) А∩В∩С.

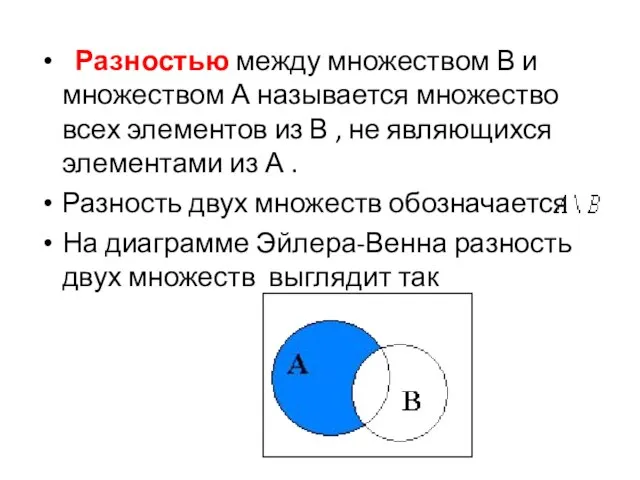
Разностью между множеством В и множеством А называется множество всех элементов из В , не являющихся элементами из А .
Разность двух множеств обозначается
На диаграмме Эйлера-Венна разность двух множеств выглядит так

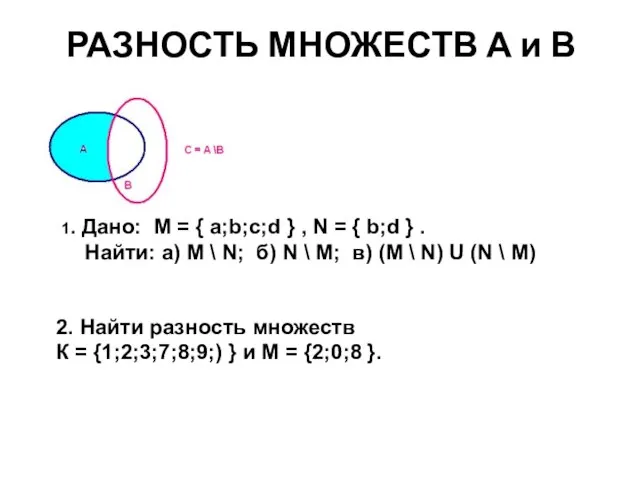
РАЗНОСТЬ МНОЖЕСТВ А и В
1. Дано: M = { a;b;c;d } , N = { b;d } .
Найти: а) M \ N; б) N \ M; в) (M \ N) U (N \ M)
2. Найти разность множеств
К = {1;2;3;7;8;9;) } и М = {2;0;8 }.