Множества. Операции над множествами

основатель теории множеств
Георг Кантор
«Множество есть многое, мыслимое нами как единое»

Понятия теории множеств
Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в математику немецким ученым Георгом Кантором (1845-1918).Следуя Кантору, понятие "множество" можно определить так:
Множество- совокупность объектов, обладающих определенным свойством, объединенных в единое целое.

Придумай название для предметов и животных, собранных вместе:
КОЛЛЕКЦИЯ МАРОК
НАБОР КАРАНДАШЕЙ
СТАЯ ПТИЦ
ЧАЙНЫЙ СЕРВИЗ
БУКЕТ ЦВЕТОВ
СТАДО КОРОВ

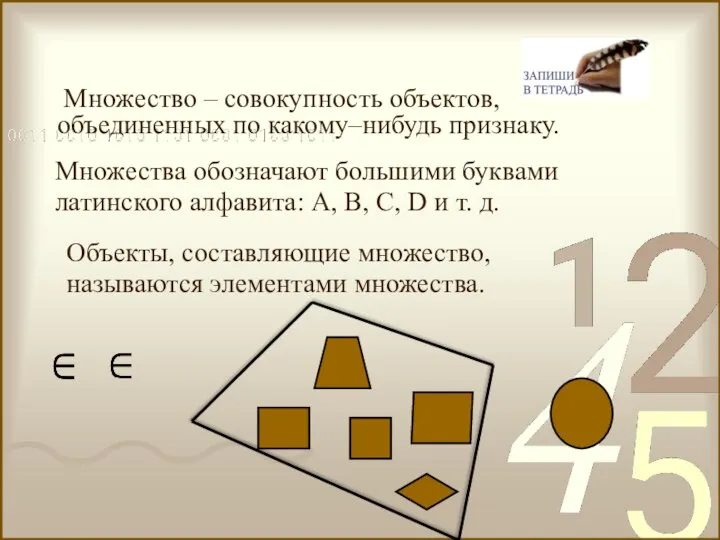
Множество – совокупность объектов, объединенных по какому–нибудь признаку.
Объекты, составляющие множество, называются элементами множества.
Множества обозначают большими буквами латинского алфавита: А, В, С, D и т. д.

Множество четырехугольников
Пространственные тела
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…
Квадраты чисел
Цифры десятичной системы счисления
10, 12, 14, 16 … 96, 98

множество людей на Солнце
множество прямых углов равностороннего треугольника
множество точек пересечения двух параллельных прямых
Пустое множество- множество, не содержащее ни одного элемента.

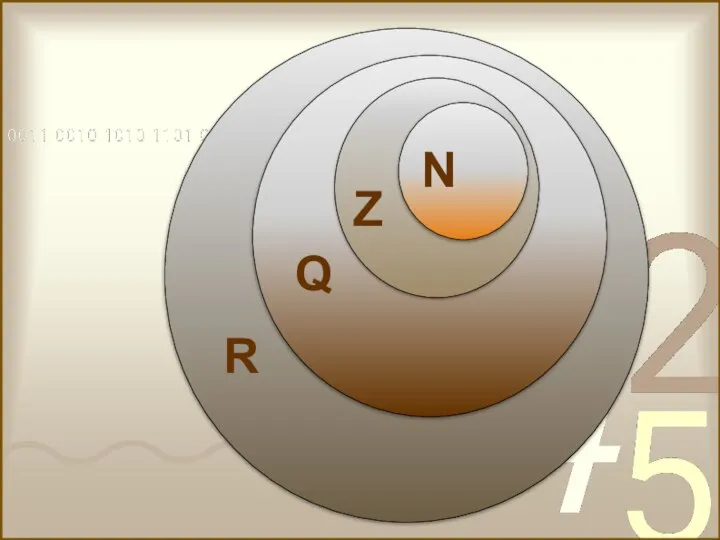
Обозначения некоторых числовых множеств:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I - множество иррациональных чисел;
R – множество действительных чисел.

Запишите множества букв слов
КОНИ И КИНО
ВИДЫ МНОЖЕСТВ
Равные множества
{К, О, Н, И}
{К, И, Н, О}

А = {2; 3; 5; 7; 11; 13};
{х | 5< х <12}
ВИДЫ МНОЖЕСТВ
Конечные множества

{1; 4; 9; 16; 25; …};
{10; 20; 30; 40; 50; …};
ВИДЫ МНОЖЕСТВ
Бесконечные множества

Среди перечисленных ниже множеств укажите конечные и бесконечные множества:
а) множество чисел, кратных 13;
б) множество делителей числа 15;
в) множество деревьев в лесу;
г) множество натуральных чисел;
д) множество рек Крыма;
е) множество корней уравнения х + 3 = 11;
ж) множество решений неравенства х + 1 < 3.

Задайте множество цифр, с помощью которых записывается число:
а) 3254; б) 8797; в) 11000; г) 555555.
Охарактеризуйте множество А:
а) А = {1, 3, 5, 7, 9};
б) А = {- 2, - 1, 0, 1, 2};
в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99};

1. В множестве {лев; лисица; гиена; слон; рысь} все элементы, кроме одного, обладают некоторым свойством.
а) опишите это свойство;
б) найдите элемент, не обладающий этим свойством;
в) назовите еще два элемента, обладающие этим свойством.
2. Назовите 5 подмножеств в множестве всех цветов радуги.
3. Каким свойством в множестве ромбов выделяется подмножество квадратов?

А – четные натуральные числа
В – двузначные числа
Найти объединение этих множеств.
А В – быть четным натуральным или двузначным числом
Пример: 8 и 32

БЛИЦ-ОПРОС

БЛИЦ-ОПРОС
земноводные, млекопитающие, хладнокровные и т.п.
Какие названия применяются для обозначения множеств животных?

БЛИЦ-ОПРОС
букет
Как называется множество цветов, стоящих в вазе?

БЛИЦ-ОПРОС
экватор
Как называется множество точек земной поверхности, равноудаленных от обоих полюсов?

БЛИЦ-ОПРОС
деревня, село, город, посёлок
Как называется множество населённых людьми мест?

БЛИЦ-ОПРОС
выставка, галерея
Как называется множество картин?

БЛИЦ-ОПРОС
архив
Как называется множество документов?

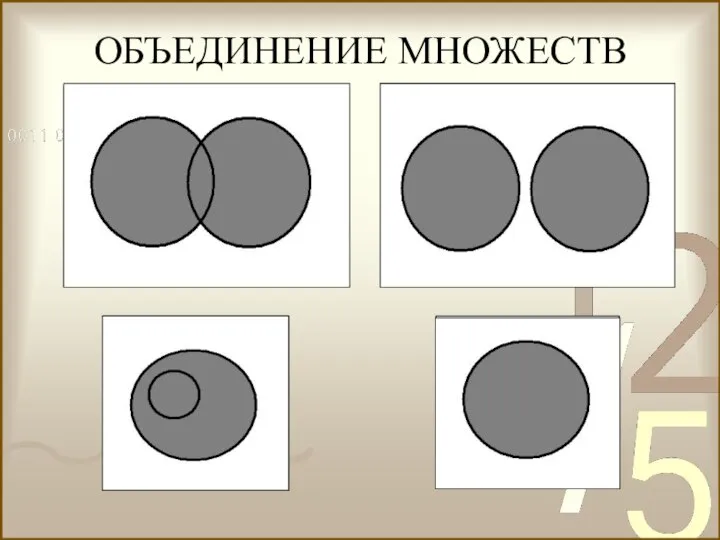
Объединением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А или В.
Объединение множеств обозначается
П р и м е р : {1,2,3} {2,3,4} = {1,2,3,4}.

ОБЪЕДИНЕНИЕ МНОЖЕСТВ

А – четные натуральные числа
В – двузначные числа
Найти объединение этих множеств.
А В – быть четным натуральным или двузначным числом
Пример: 8 и 32

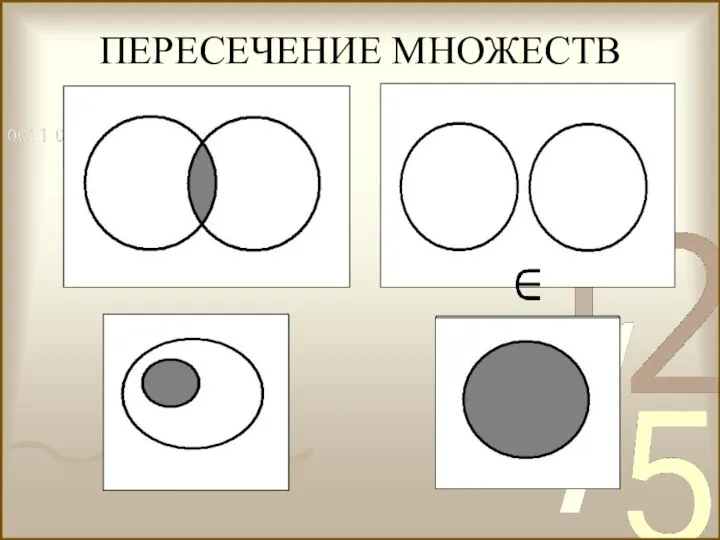
Пересечением множеств А и В называется множество, содержащее все элементы, которые принадлежат множествам А и В одновременно.
Пересечение множеств обозначается
П р и м е р : {1,2,3} {2,3,4} = {2,3}

ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ

А – четные натуральные числа
В – двузначные числа
Найти пересечение этих множеств. А В – быть четным натуральным и двузначным числом
Пример: 32

Даны множества:
А = {2; 3; 8},
В = {2; 3; 8; 11},
С = {5; 11}.
Найдите: 1) АUВ; 2) АUС; 3) СUВ.

Даны множества:
А = {a, b, c, d},
B = {c, d, e, f},
C = {c, e, g, k}.
Найдите: (АUВ)UС.