Формулы для радиусов вписанной и описанной окружностей треугольника

Определение: окружность называется вписанной в треугольник,
если все стороны треугольника касаются окружности.
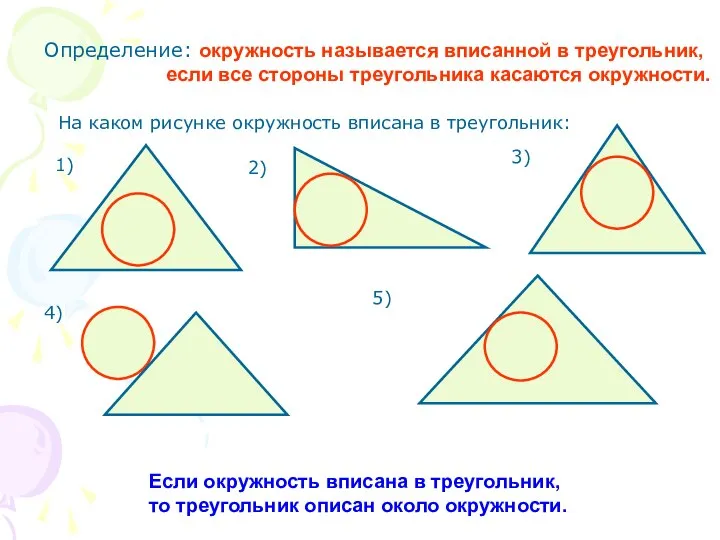
Если окружность вписана в треугольник,
то треугольник описан около окружности.

Расположение центров окружностей, описанных около треугольника.
Центр окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника.
Если треугольник остроугольный, то центр окружности расположен в этом треугольнике.

Расположение центров окружностей, описанных около треугольника.
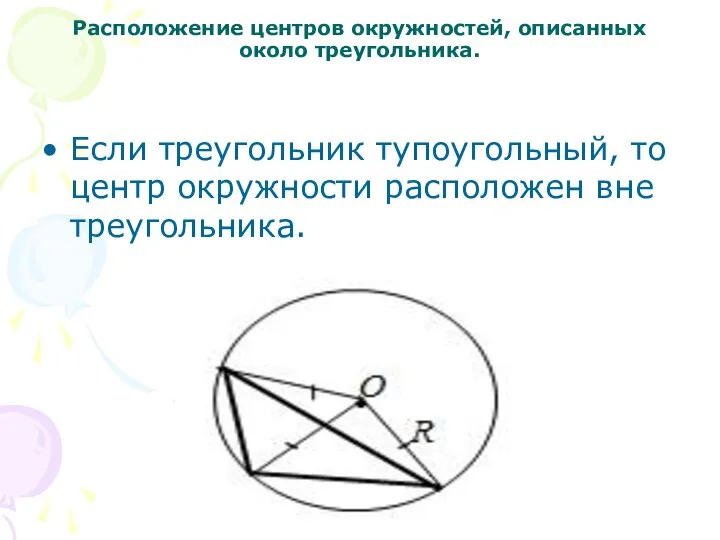
Если треугольник тупоугольный, то центр окружности расположен вне треугольника.

Расположение центров окружностей, описанных около треугольника.
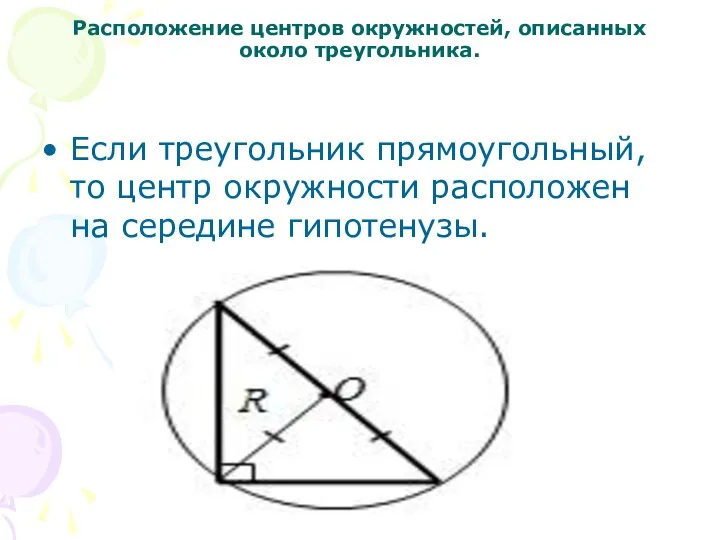
Если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы.

Расположение центров окружностей, описанных около треугольника.
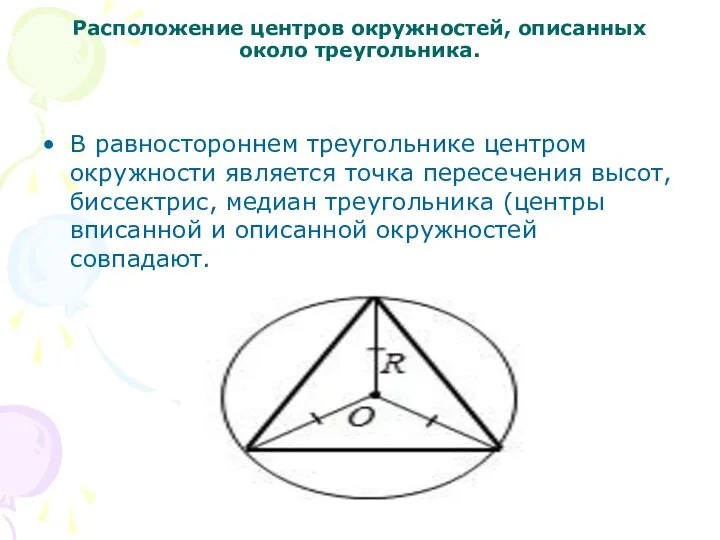
В равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают.

Расположение центров окружностей, описанных около треугольника.
В равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию.

Формулы для вычисления радиуса описанной окружности

Расположение центров окружностей, вписанных в треугольник
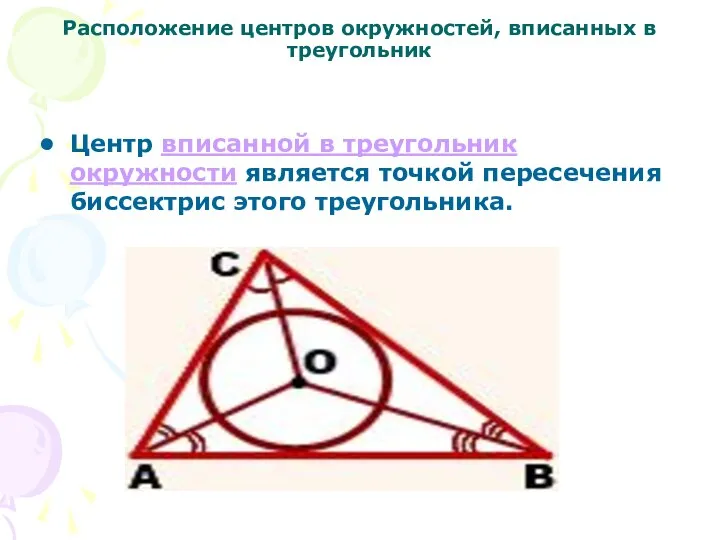
Центр вписанной в треугольник окружности является точкой пересечения биссектрис этого треугольника.

Расположение центров окружностей, вписанных в треугольник

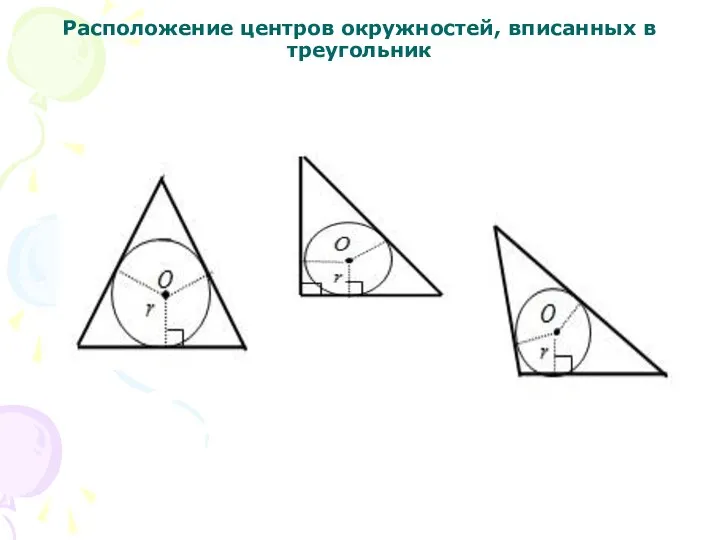
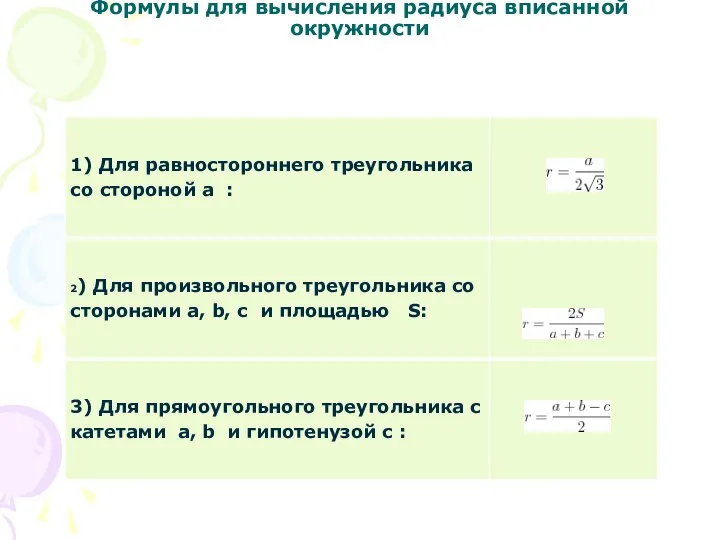
Формулы для вычисления радиуса вписанной окружности
.

Расположение центров вписанных окружностей в треугольник .
Центр вписанной окружности — точка пересечения биссектрис треугольника, ее радиус r вычисляется по формуле: : r = ,
где S — площадь треугольника,а p- полупериметр.
полупериметр.

Особый случай – правильный треугольник
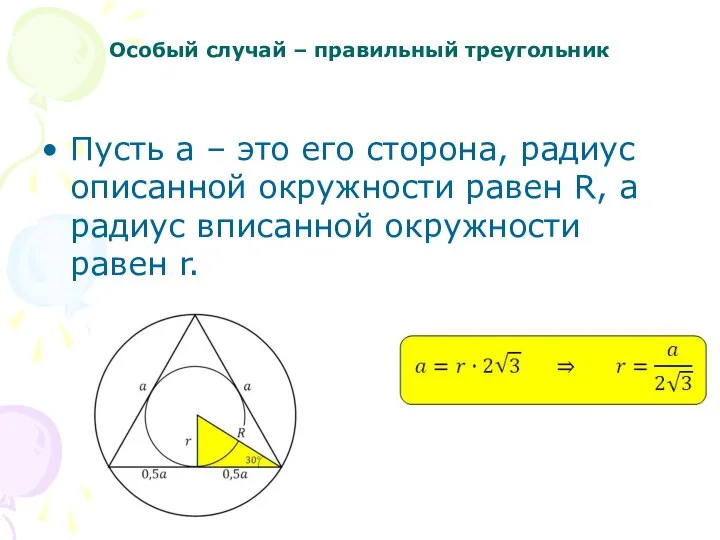
Пусть а – это его сторона, радиус описанной окружности равен R, а радиус вписанной окружности равен r.

Задача1 : в равносторонний треугольник со стороной 4 см
вписана окружность. Найдите её радиус.
Решение:

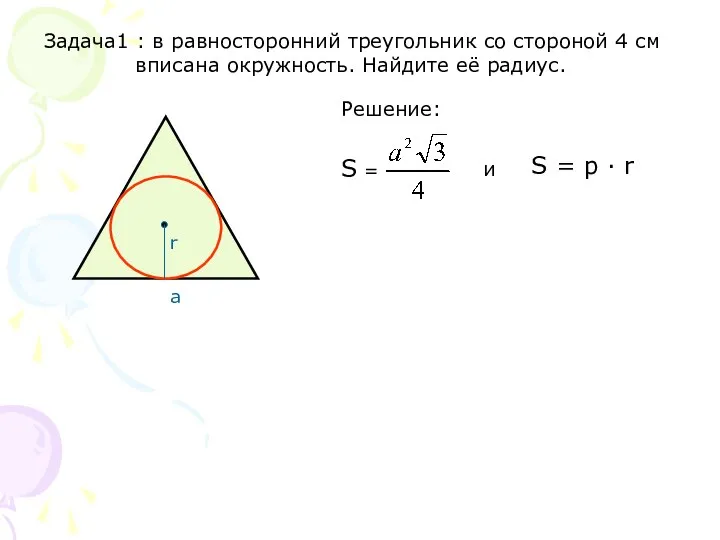
Задача 2 : в прямоугольный треугольник вписана окружность,
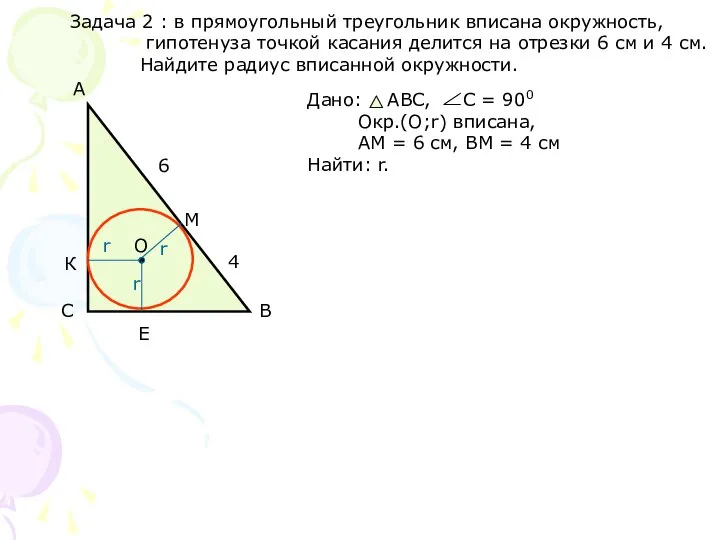
гипотенуза точкой касания делится на отрезки 6 см и 4 см.
Найдите радиус вписанной окружности.