Содержание
- 2. Лекция 1. Введение в начертательную геометрию Предмет и задачи начертательной геометрии Виды проецирования Ортогональная система плоскостей
- 3. - НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ - наука о способах изображения пространственных форм на плоскости или другой поверхности и
- 4. Задачи НГ: Построение изображений объемных форм, имеющих три измерения на плоскости, имеющей два измерения Чтение изображений,
- 5. Проецирование – процесс получения на чертеже достоверного изображения, по которому можно представить форму и размеры объекта
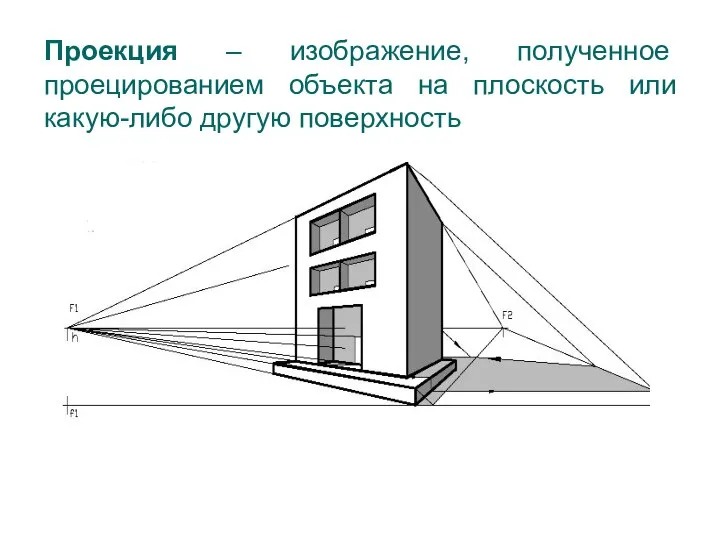
- 7. Проекция – изображение, полученное проецированием объекта на плоскость или какую-либо другую поверхность
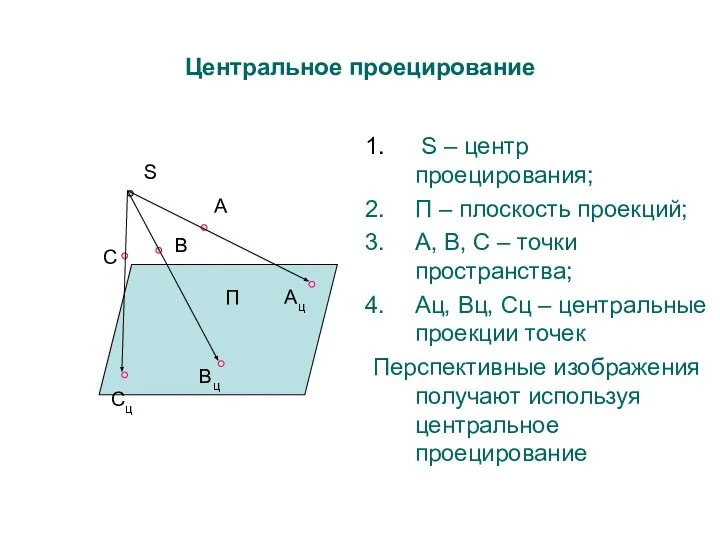
- 8. S – центр проецирования; П – плоскость проекций; А, В, С – точки пространства; Ац, Вц,
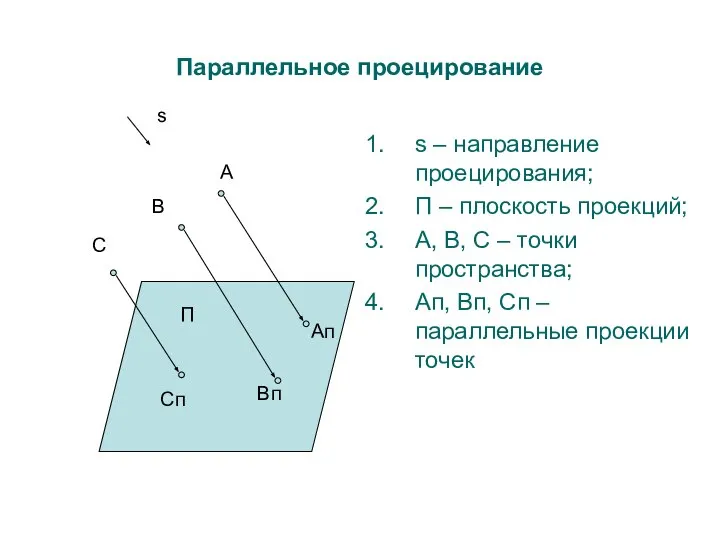
- 9. Параллельное проецирование s – направление проецирования; П – плоскость проекций; А, В, С – точки пространства;
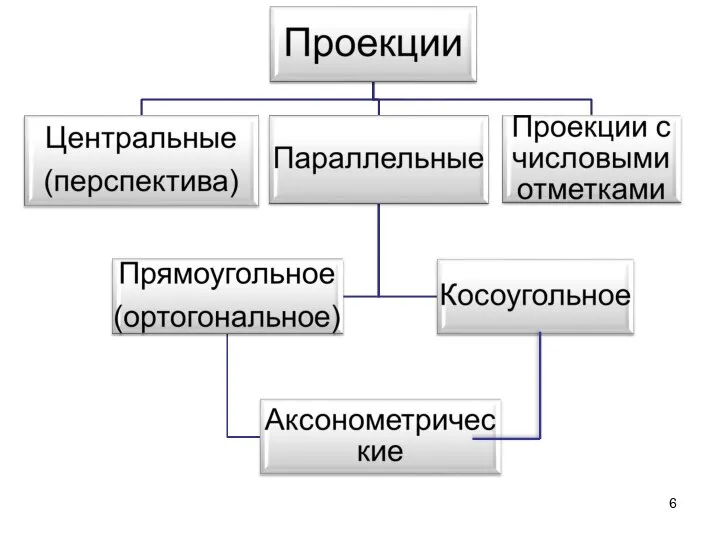
- 10. ПАРАЛЛЕЛЬНЫЕ ПРОЕКЦИИ: Прямоугольные – если проецирующие лучи направлены к плоскости проекций под прямым углом Косоугольные -
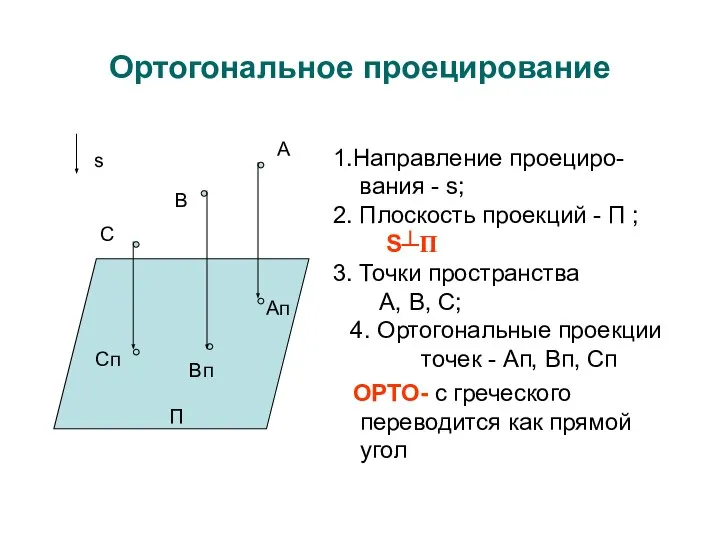
- 11. Ортогональное проецирование Вп Сп С В А П s Ап 1.Направление проециро- вания - s; 2.
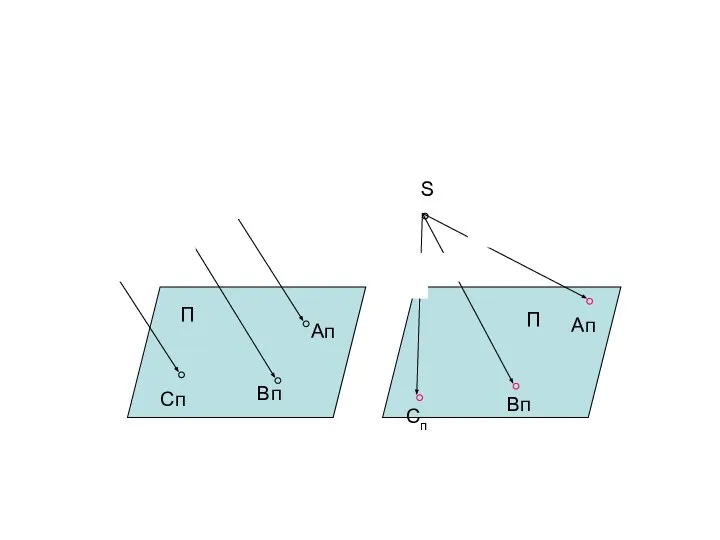
- 12. Ап Вп Сп С В А П S А П В С Сп Ап Вп
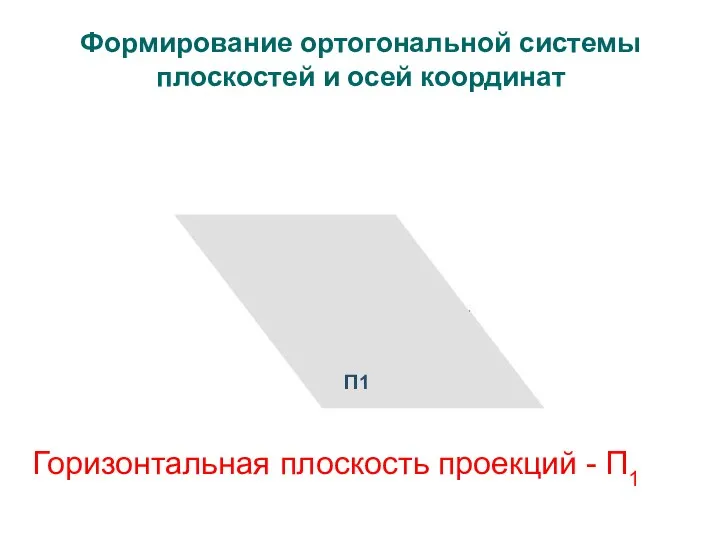
- 13. Формирование ортогональной системы плоскостей и осей координат П1 Горизонтальная плоскость проекций - П1
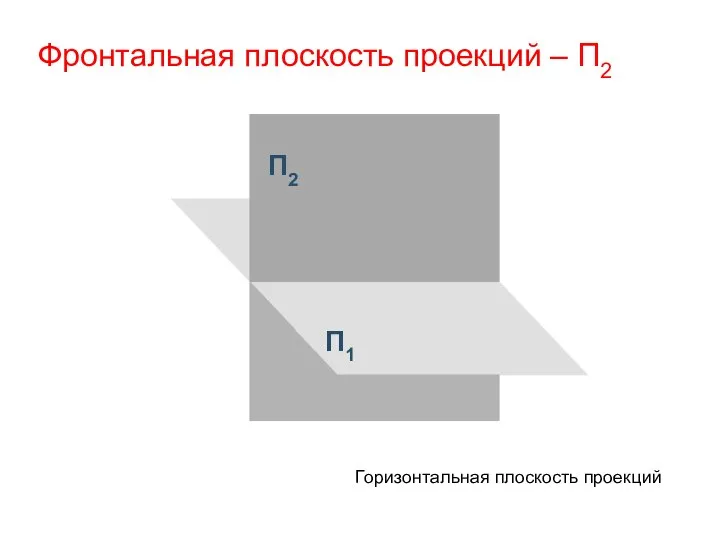
- 14. П2 П1 Горизонтальная плоскость проекций Фронтальная плоскость проекций – П2
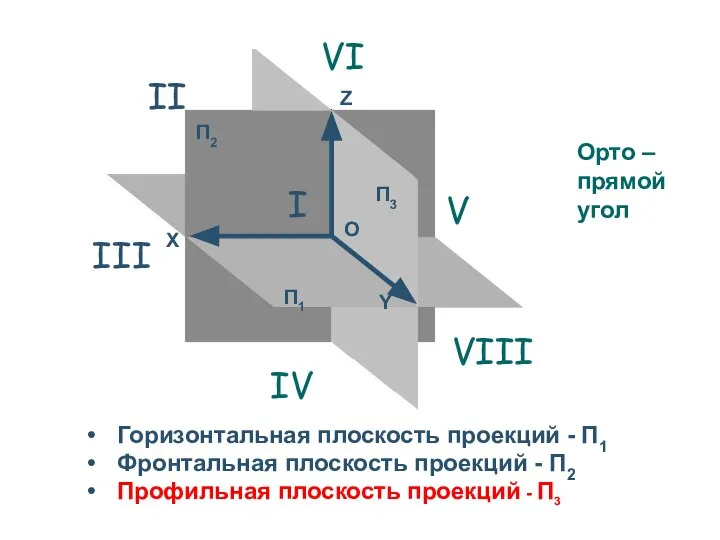
- 15. Горизонтальная плоскость проекций - П1 Фронтальная плоскость проекций - П2 Профильная плоскость проекций - П3 П2
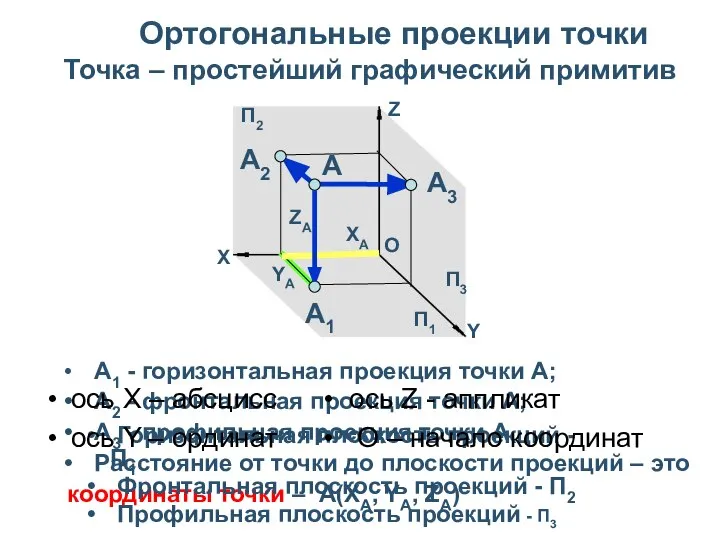
- 16. Ортогональные проекции точки А1 - горизонтальная проекция точки А; А2 - фронтальная проекция точки А; А3
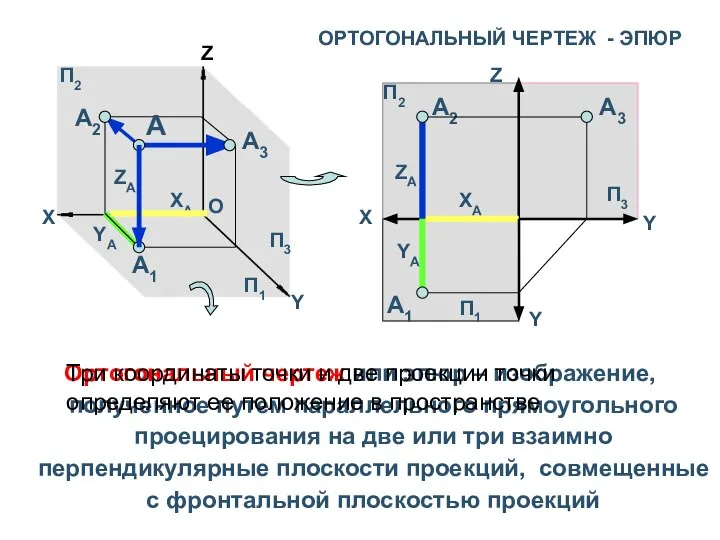
- 17. ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ - ЭПЮР Ортогональный чертеж или эпюр – изображение, полученное путем параллельного прямоугольного проецирования на
- 18. Понятие о четвертях и октантах Четверть – двугранный угол, образованный в пересечении плоскостей П1 и П2
- 19. СВОЙСТВА ОРТОГОНАЛЬНЫХ ПРОЕЦИЙ ТОЧКИ: Две разноименные проекции точки расположены на одной линии связи По двум проекциям
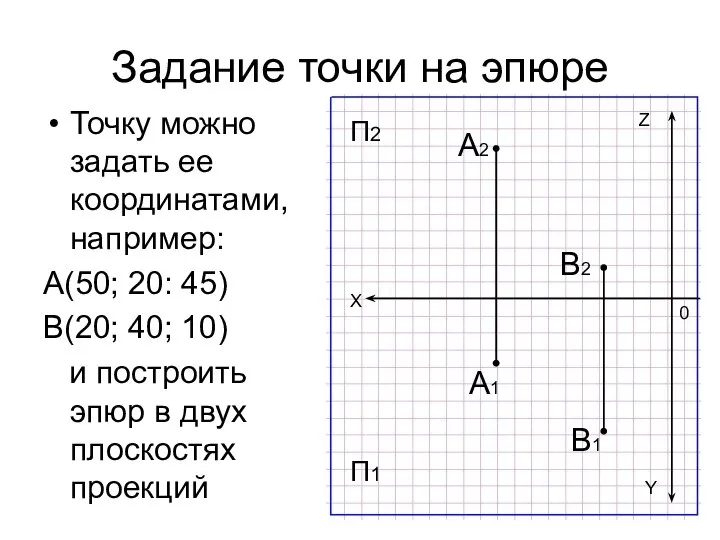
- 20. Задание точки на эпюре Точку можно задать ее координатами, например: А(50; 20: 45) В(20; 40; 10)
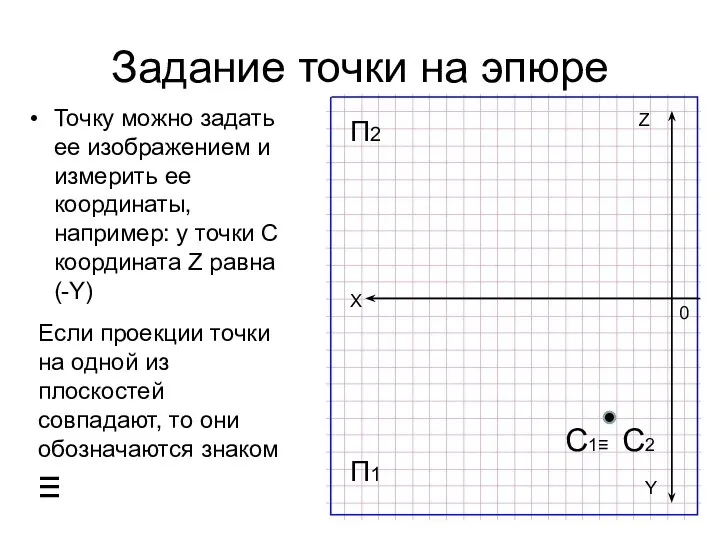
- 21. Задание точки на эпюре Точку можно задать ее изображением и измерить ее координаты, например: у точки
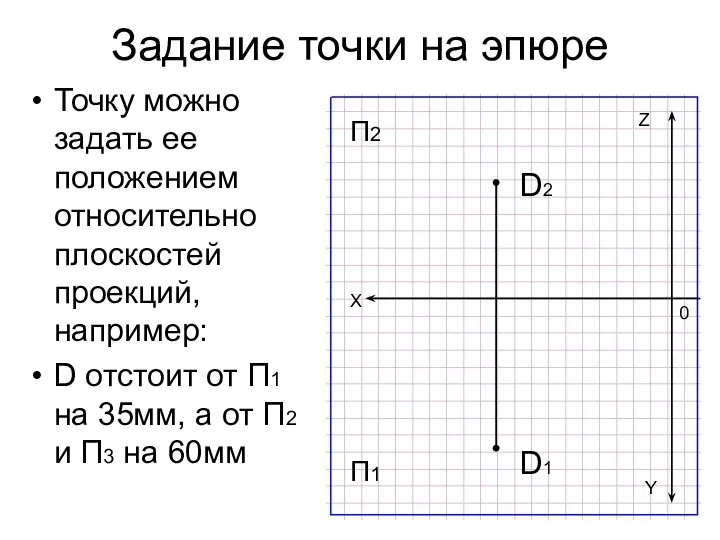
- 22. Задание точки на эпюре Точку можно задать ее положением относительно плоскостей проекций, например: D отстоит от
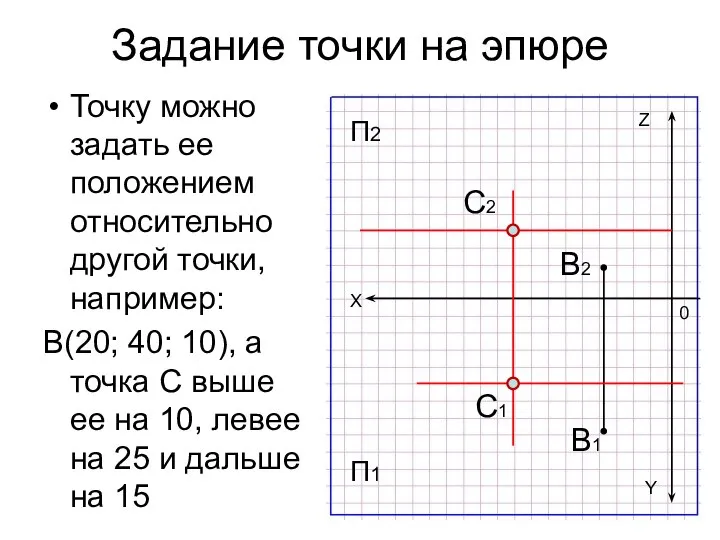
- 23. Задание точки на эпюре Точку можно задать ее положением относительно другой точки, например: В(20; 40; 10),
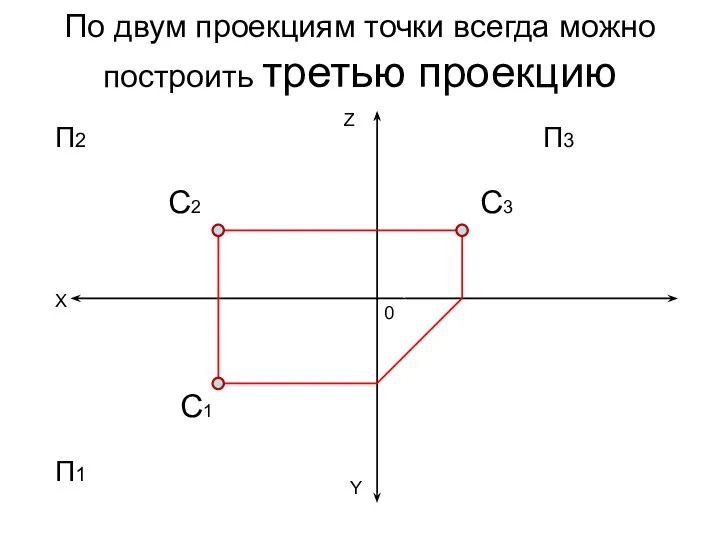
- 24. По двум проекциям точки всегда можно построить третью проекцию X Z Y 0 П1 П2 С2
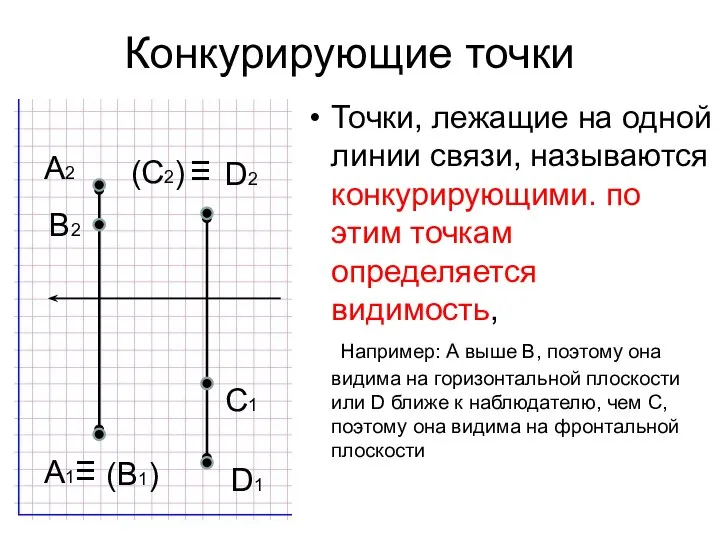
- 25. Конкурирующие точки Точки, лежащие на одной линии связи, называются конкурирующими. по этим точкам определяется видимость, Например:
- 27. Скачать презентацию







 Из истории геометрии
Из истории геометрии Предел последовательности. Лекция 3
Предел последовательности. Лекция 3 Метод корреляционных плеяд
Метод корреляционных плеяд Уравнения и неравенства с двумя переменными, содержащие параметр
Уравнения и неравенства с двумя переменными, содержащие параметр Решение уравнений, содержащих переменную под знаком модуля
Решение уравнений, содержащих переменную под знаком модуля Урок математики в 5 классе
Урок математики в 5 классе Объем прямоугольного параллелепипеда. Объем прямой призмы
Объем прямоугольного параллелепипеда. Объем прямой призмы Нас окружают числа. Факультет космических исследований МГУ имени М.В.Ломоносова
Нас окружают числа. Факультет космических исследований МГУ имени М.В.Ломоносова Методы общения линейных уравнений с тремя неизвестными
Методы общения линейных уравнений с тремя неизвестными Скалярное произведение векторов
Скалярное произведение векторов Численность населения города Кингисепп и Кингисеппского района в различные периоды времени.(4 класс)
Численность населения города Кингисепп и Кингисеппского района в различные периоды времени.(4 класс) Параллельность плоскостей
Параллельность плоскостей Презентация на тему Функция арифметического квадратного корня, её свойства
Презентация на тему Функция арифметического квадратного корня, её свойства  2.7. Теория систем линейных алгебраических уравнений
2.7. Теория систем линейных алгебраических уравнений Скалярное произведение векторов. (Лекция 5)
Скалярное произведение векторов. (Лекция 5) Параллельность прямых в пространстве
Параллельность прямых в пространстве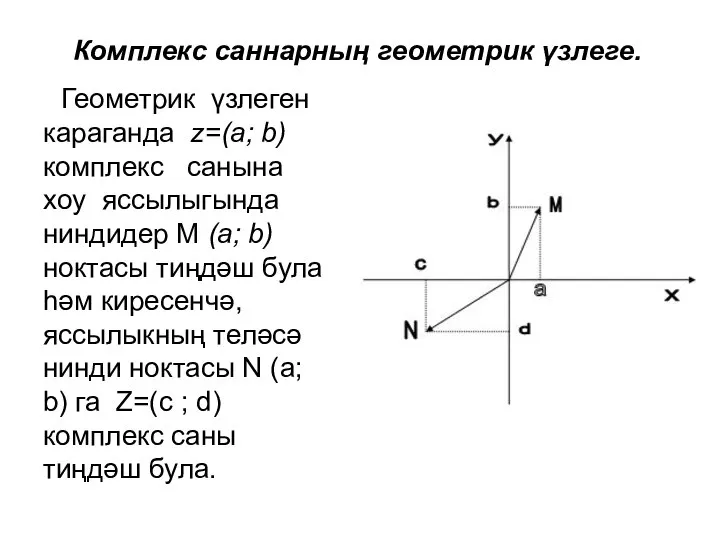 Комплекс саннарның геометрик үзлеге
Комплекс саннарның геометрик үзлеге Сумма
Сумма Подготовка к диагностической работе
Подготовка к диагностической работе Сфера, описанная вокруг многогранника
Сфера, описанная вокруг многогранника Векторный анализ - теория поля. Векторное поле. Лекция 17
Векторный анализ - теория поля. Векторное поле. Лекция 17 Правило произведения. Комбинаторика
Правило произведения. Комбинаторика Математическое моделирование. Рандомизация
Математическое моделирование. Рандомизация Шар. Куб. Параллелепипед
Шар. Куб. Параллелепипед Решение задач. Подготовка к умножению
Решение задач. Подготовка к умножению Повторение. Числа от 100 до 1000 (Урок 1)
Повторение. Числа от 100 до 1000 (Урок 1) Первообразная и интеграл
Первообразная и интеграл Многоугольники
Многоугольники