позволяет свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки или методом замены переменной. Он основан на следующей теореме:
Теорема. Пусть функция определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула
Метод замены переменной обычно применяется, когда подынтегральное выражение представляет собой независимую переменную, умноженную на многочлен от этой переменной, или на тригонометрическую функцию от этой переменной или на степенную функцию (в том числе корень) от этой переменной.






 Задания по математике (5 класс, часть 3)
Задания по математике (5 класс, часть 3) Задания Незнайки
Задания Незнайки Алгоритм как один из приемов в формировании учебно-познавательной компетенции на уроках математики
Алгоритм как один из приемов в формировании учебно-познавательной компетенции на уроках математики Решение задач и уравнений
Решение задач и уравнений Нелинейные уравнения и системы нелинейных алгебраических уравнений. Лекция 4
Нелинейные уравнения и системы нелинейных алгебраических уравнений. Лекция 4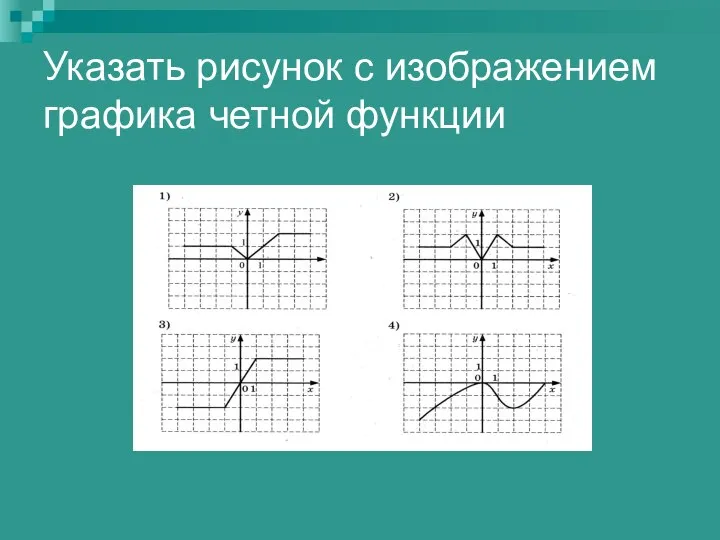 Указать рисунок с изображением графика четной функции
Указать рисунок с изображением графика четной функции В гостях у геометрических фигур
В гостях у геометрических фигур Объем прямоугольного параллелепипеда. Объем прямой призмы
Объем прямоугольного параллелепипеда. Объем прямой призмы Реши примеры устно. 2 класс
Реши примеры устно. 2 класс Признаки подобия треугольников
Признаки подобия треугольников Линейная функция. Работа по графику
Линейная функция. Работа по графику Координаты вектора в пространстве. 12 кл
Координаты вектора в пространстве. 12 кл Дополняем до круглого числа
Дополняем до круглого числа Графики функций
Графики функций Окружность. Методическая разработка урока
Окружность. Методическая разработка урока Решение уравнений. Подготовка к ОГЭ
Решение уравнений. Подготовка к ОГЭ Презентация на тему Натуральные числа 5 класс
Презентация на тему Натуральные числа 5 класс  Математический КВН. 6 класс
Математический КВН. 6 класс Презентация на тему Факториал 9 класс
Презентация на тему Факториал 9 класс  Метод координат на плоскости
Метод координат на плоскости Ряд Тейлора функции многих переменных. Лекция 19
Ряд Тейлора функции многих переменных. Лекция 19 Откуда к нам пришли отрицательные числа? Сказка бабушки Тортилы
Откуда к нам пришли отрицательные числа? Сказка бабушки Тортилы Значение логического выражения (тема № 3)
Значение логического выражения (тема № 3) Математическое обеспечение (МО) цифрового (автоматизированного) проектирования
Математическое обеспечение (МО) цифрового (автоматизированного) проектирования Зачёт по таблице умножения
Зачёт по таблице умножения Сравнение натуральных чисел
Сравнение натуральных чисел Движение в пространстве
Движение в пространстве Промежуточная аттестация по геометрии
Промежуточная аттестация по геометрии