Накопленная частота и др

Предположим, есть список чисел, представляющий собой количество книг, которые каждый студент прочитал за последний месяц.
После сортировки у нас получился следующий набор чисел: 3, 3, 5, 6, 6, 6, 8.

3, 3, 5, 6, 6, 6, 8
вверху левой колонки пишем “Количество книг”, а вверху правой колонки — “Частота”.
Во второй строке пишем первое количество прочитанных книг, то есть число 3, во второй строке колонки “Частота” пишем цифру 2.

Накопленная частота отвечает на вопрос "сколько раз встречается в списке данное значение или меньшая величина?".
Всегда начинайте с наименьшего значения в наборе данных.
Поскольку в нашем примере нет меньших значений, для данной величины
накопленная частота
равна
абсолютной.

Чтобы определить накопленную частоту для второго значения списка, необходимо прибавить его абсолютную частоту к накопительной частоте предыдущего значения.
Иными словами, следует взять последнюю накопленную частоту и прибавить к ней абсолютную частоту данной величины.

Проверьте полученные результаты:
В итоге мы сложили абсолютные частоты всех значений списка.
Конечная наколенная частота должна соответствовать числу значений в списке.
Есть два способа проверить, так ли это:
Сложим абсолютные частоты всех значений:
2 + 1 + 3 + 1 = 7, в результате получится накопленная частота.
Посчитаем число значений в наборе данных.
В нашем примере список имел следующий вид: 3, 3, 5, 6, 6, 6, 8.
В этом списке семь величин, и итоговая накопленная частота также равна 7.

Дискретные данные
Дискретные данные можно посчитать, они не дробятся на более мелкие составляющие.
Количество собак является дискретным множеством.
Нет такого понятия, как половина собаки.

Непрерывные данные
Непрерывные данные часто не поддаются конечному счету, между двумя произвольными величинами обязательно найдутся другие возможные значения.
Высота снега представляет собой непрерывное множество.
Высота снега возрастает постепенно и непрерывно, а не на дискретные величины.
Если вы измерите высоту снега в сантиметрах, то точное значение может оказаться, например, 20,6 сантиметра.

Частости – это…
Существуют относительные показатели, характеризующие долю частоты отдельных вариантов в общей сумме частот.
Эти относительные показатели именуют частостями и условно обозначают через ,
т.е. .
Сумма всех частостей равна единице.
Частости могут быть выражены и в процентах, и тогда их сумма будет равна 100%.

Мода и медиана
Мода – это величина признака (варианта), которая чаще всего встречается в данной совокупности, т.е. имеет наибольшую частоту.
Мода имеет большое практическое применение и в ряде случаев только мода может дать характеристику общественных явлений.
Медиана – это варианта, которая находится в середине упорядоченного (ранжированного) вариационного ряда.
Рассмотрим расчет моды и медианы в дискретном вариационном ряду:

Определить моду и медиану:
Мода Мо = 4 года, так как этому значению соответствует наибольшая частота f = 5.
Т.е. наибольшее число рабочих имеют стаж 4 года.

Медиана
Для того, чтобы вычислить медиану, найдем предварительно половину суммы частот. Если сумма частот является числом нечетным, то мы сначала прибавляем к этой сумме единицу, а затем делим пополам:
Ме=16/2=8
Медианой будет восьмая по счету варианта.
Для того, чтобы найти, какая варианта будет восьмой по номеру, будем накапливать частоты до тех пор, пока не получим сумму частот, равную или превышающую половину суммы всех частот. Соответствующая варианта и будет медианой.

Медиана
Ме = 4 года.
Т.е. половина рабочих имеет стаж меньше четырех лет, половина больше.
Если сумма накопленных частот против одной варианты равна половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.

Свойство медианы
Главное свойство Ме в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой
другой величины: .
Это свойство Ме может быть использовано, например, при определении места строительства общественных зданий, т.к. Ме определяет точку, дающую наименьшее расстояние, допустим, детских садов от местожительства родителей, жителей населенного пункта от кинотеатра, при проектировке трамвайных, троллейбусных остановок и т.д.

Медиана. Пример 2:
Найти медиану дискретного ряда
16,13,15,10,19,22,25,12,18,14,19,14,16,10.
Решение. Ранжируем ряд: 10,10,12,13,14,14,15,16,16,18,19,19,22,25, выборка содержит четное число элементов n=14, следовательно медиана лежит между двумя средними элементами выборки - между 7-элементом и 8-элементом:
10,10,12,13,14,14,15,16,16,18,19,19,22,25
и равна среднему арифметическому этих элементов:
Me=(15+16)/2=15,5

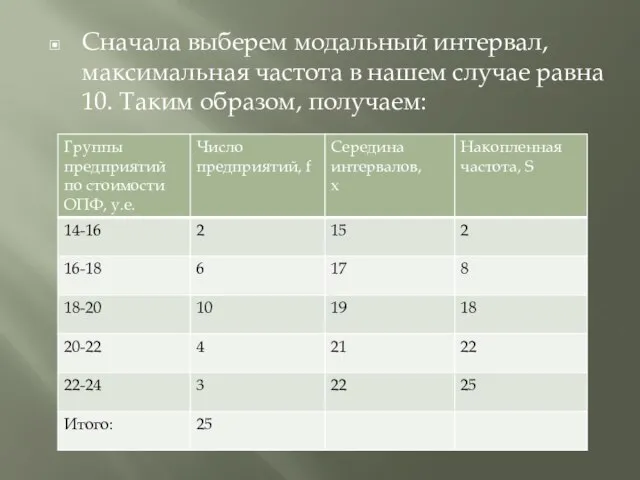
Сначала выберем модальный интервал, максимальная частота в нашем случае равна 10. Таким образом, получаем:

Мода. Расчеты
1) По максимальной частоте найдем модальный интервал: Fmax=10 → I = 18-20
2) По соответствующей формуле
Мода =18+2*(10-6)/(10-6)(10-4)=18,33 млн. руб. – наиболее часто встречающаяся стоимость ОПФ среди 25 предприятий.

Медиана. Расчеты:
Нам даны интервалы.
1) Найдем медианный интервал по накопленной частоте. Нужная накопленная частота определяется путем суммирования частот f до тех пор, пока очередная накопленная частота впервые не превысит половину совокупности n +1/2 или n/2.
Для нечетного ряда (25+1)/2= 13→S= 18 →18-20- медианный интервал, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части.

Медиана. Расчеты:
2) По соответствующей формуле
Медиана Ме =18+2[(25+1)/2 - 8/10]=18,9 млн.руб.
Из 25 малых предприятий региона 12 пр. имеют стоимость ОПФ менее 18 млн.руб., а 12 пр. более.

Медиана. Пример 3:

Решение:
Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта,
которая делит совокупность
на две равные части
(Σfi/2 = 3462/2 = 1731).

Решение:
Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:
Это значит что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.