Задача Иосифа Флавия

Цели:

Задачи:

Из истории…
Иосиф Флавий - известный историк первого века - выжил и стал известным благодаря математической одаренности. В ходе иудейской войны он в составе отряда из 41 иудейского воина был загнан римлянами в пещеру. Предпочитая самоубийство плену, воины решили выстроиться в круг и последовательно убивать каждого третьего из живых до тех пор, пока не останется ни одного человека. Однако Иосиф наряду с одним из своих единомышленников счел подобный конец бессмысленным - он быстро вычислил спасительные места
в порочном круге, на которые поставил себя и своего товарища.

Задача Иосифа Флавия
Расставим натуральные числа по кругу от 1 до 41 и вычеркиваем каждое второе число до тех пор, пока не останется одно число. Это и будет решение задачи.
Условие
2
3
4
5
6
7
9
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
1
8
39
38
10
40
41
19

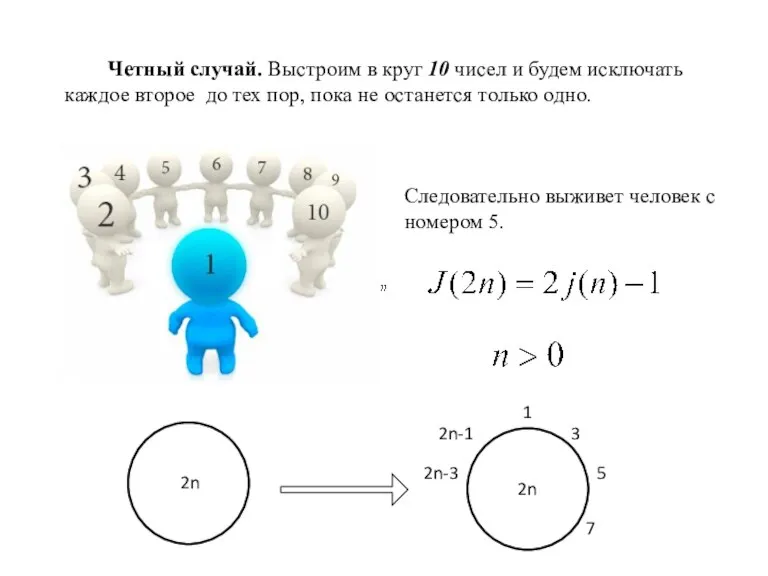
Четный случай. Выстроим в круг 10 чисел и будем исключать каждое второе до тех пор, пока не останется только одно.
Следовательно выживет человек с номером 5.

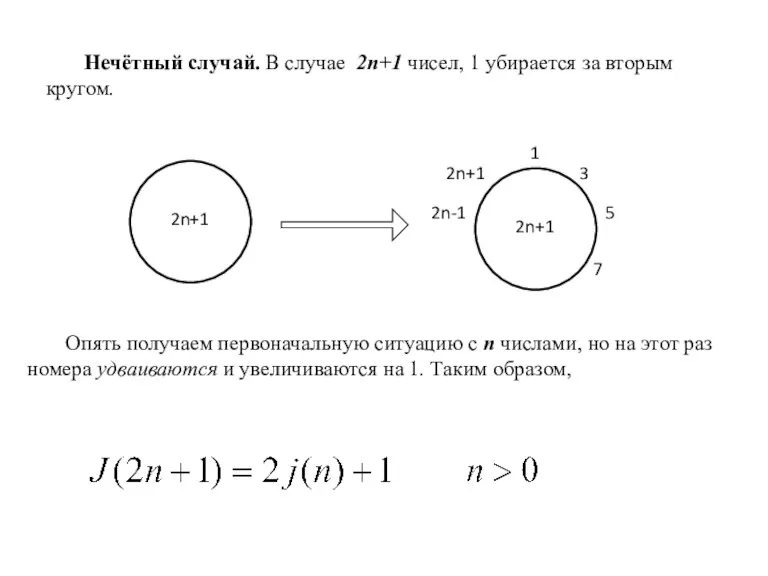
Нечётный случай. В случае 2n+1 чисел, 1 убирается за вторым кругом.
2n+1
Опять получаем первоначальную ситуацию с n числами, но на этот раз
номера удваиваются и увеличиваются на 1. Таким образом,

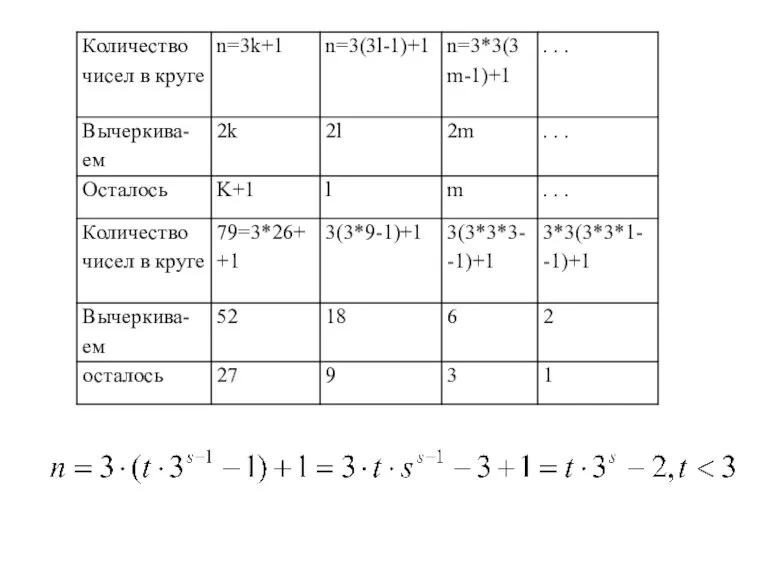
Рекуррентное соотношение дает возможность очень быстро составить таблицу первых значений J(n).
Если сгруппировать значения n по степеням 2 (в таблице эти группы отделены вертикальными линиями), то в каждой группе J(n) всегда будет начинаться с 1, а затем увеличиваться на 2.

Решим другую задачу:
Расставим натуральные числа по кругу от 1 до n. Вычеркиваем числа 2, 3,
пропускаем число 4, вычеркиваем два следующих числа и т.д. Вычеркиваем
до тех пор, пока не останется одно число. Это число и будет решением задачи.
22

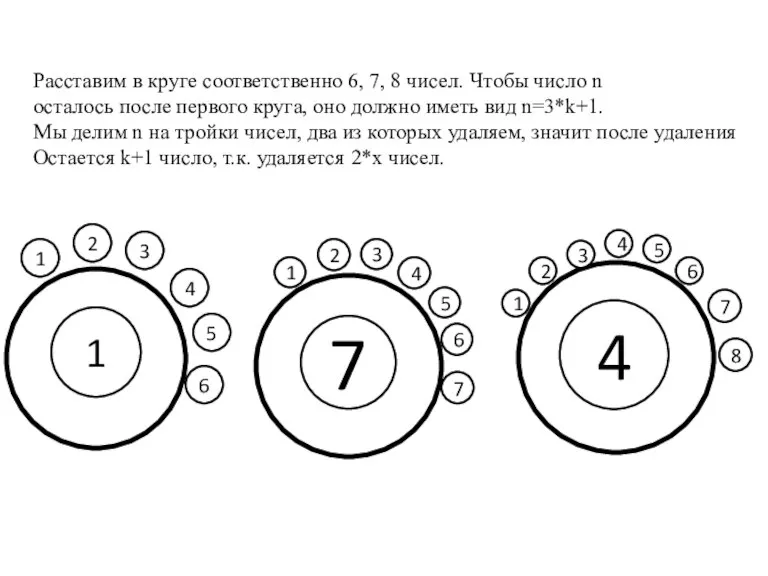
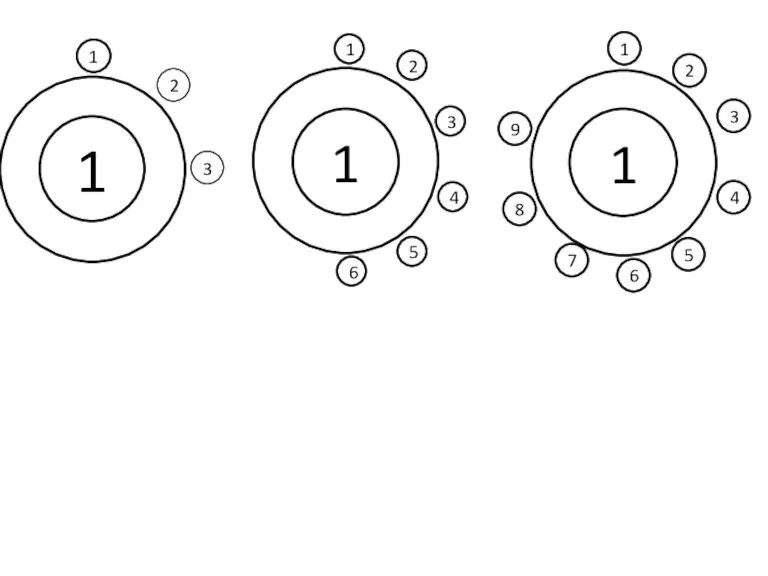
Расставим в круге соответственно 6, 7, 8 чисел. Чтобы число n
осталось после первого круга, оно должно иметь вид n=3*k+1.
Мы делим n на тройки чисел, два из которых удаляем, значит после удаления
Остается k+1 число, т.к. удаляется 2*х чисел.
2
3
4
5
6
1
1
2
3
4
5
6
7
1
7
2
3
4
5
6
7
1
8
4

3
2
1
1
1
3
2
4
5
6
1
1
2
3
4
5
6
7
8
9
1

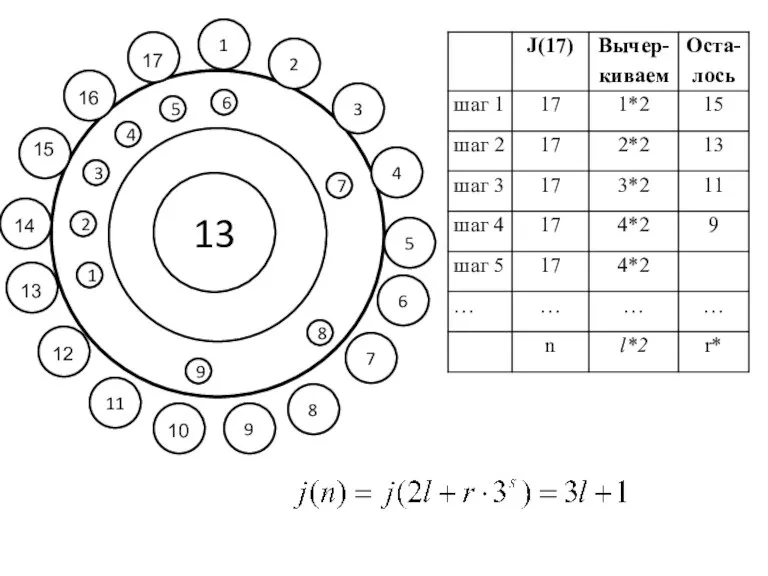
11
3
4
5
9
8
7
6
2
1
9
8
7
6
5
4
3
2
1
13

Рассмотрим табличные значения еще раз:
Пусть k=4 j(k)=j(4)=4
j(3k)=j(12)=10
j(3k+1)=j(13)=7
j(k-1)=j(3)=1
j(3k+2)=j(14)=13
Получаем рекурсивные формулы:
j(3k)=3j(k)-2
j(3k+1)=3j(k-1)+4
j(3k+2)=3j(k)+1

Доказательство полученной формулы по индукции:
1. Верность формулы при малых n проверяется подстановкой: