Метод координат на плоскости

Метод координат
на плоскости.

Лемма о коллинеарных векторах
Лемма
Доказательство:
1 случай: a↑↑b.

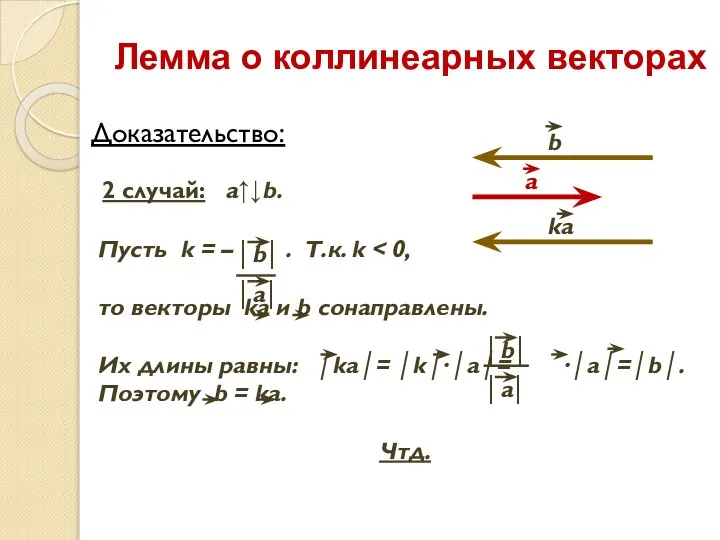
Доказательство:
Лемма о коллинеарных векторах
2 случай: a↑↓b.

Разложение вектора по двум неколлинеарным векторам

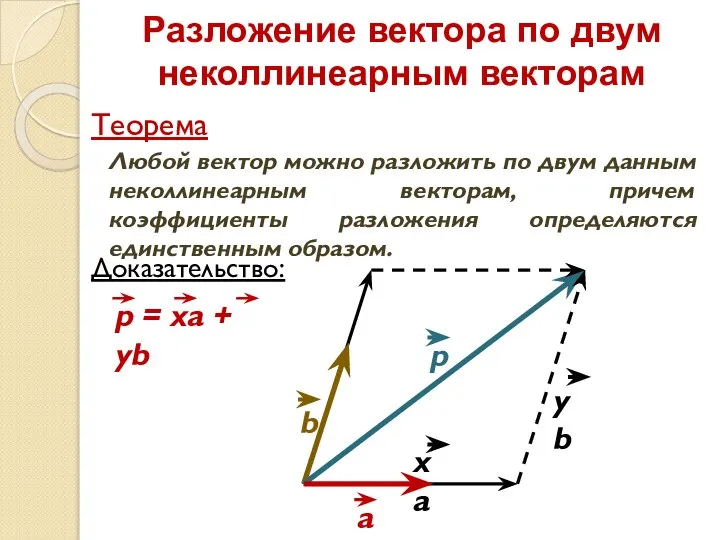
Разложение вектора по двум неколлинеарным векторам
Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.
Теорема
Доказательство:

Разобрать решение №911(а,б),
в тетрадке выполнить №911(в,г)

Разобрать решение №912(а-г),
в тетрадке выполнить №912(д-и)

Изучите тему «Координаты вектора»
посмотрев видео
и выполните задания:
№919,
№920,
№922(а,б),
№923(а,б),
№924

Выполните самостоятельную работу по вариантам, оформив следующим образом:
Самостоятельная работа по теме «Координаты вектора», выполненная учеником 9 класса _____ Ф.И.
Вариант №_____

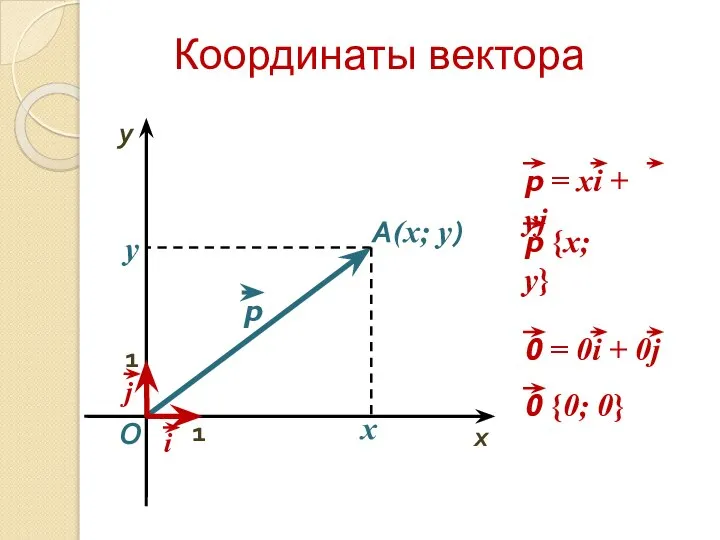
Координаты векторa
O
x
y
A(x; y)
x
y
1
1

Действия над векторами
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.