Содержание
- 2. 1. Арифметические действия над целыми числами Числа, появившиеся в результате счета, называются натуральными числами. Они обозначаются
- 3. Для натурального числа п есть противоположное число -п, а для -п противоположное п. -1, -2, -3,
- 4. Множества чисел
- 5. Над целыми числами устанавливаются действия сложения и умножения, которые обладают следующими основными свойствами: переместительное свойство сложения:
- 6. Вычитание и деление определяются как действия, обратные сложению и умножению. Вычесть из числа а число b
- 8. Целое число называется чётным, если оно делится нацело на 2, и нечётным, если оно не делится
- 9. Деление с остатком. Для любых чисел а и b (b>0) справедливо утверждение: число а всегда можно
- 10. 2. Простые и составные натуральные числа Пусть а – натуральное число. Делителем числа а называется натуральное
- 11. Натуральное число а , не равное 1, называется простым, если оно имеет только 2 делителя: 1
- 12. Основная теорема арифметики: Всякое составное натуральное число можно представить в виде произведения простых множителей и притом
- 13. 3. Признаки делимости чисел. Признак делимости на 2: число делится на 2, если его последняя цифра
- 14. Признак делимости на 4: число делится на 4, если две последние его цифры нули или образуют
- 15. Признак делимости на 8: число делится на 8, если три последние его цифры нули или образуют
- 16. Признак делимости на 3 (и 9): на 3 (или на 9), делятся только те числа, сумма
- 17. Признак делимости на 6: число делится на 6, если оно делится одновременно на 2 и на
- 18. Признак делимости на 10, 100, 1000: на 10 делятся только те числа, последняя цифра которых нуль,
- 19. Признак делимости на 11: на 11 делятся только те числа, у которых сумма цифр, занимающих нечетные
- 20. Автор: Семёнова Елена Юрьевна Обозначения
- 21. 4. Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) чисел. Наибольшее натуральное число, на которое
- 22. Примеры. Найти НОД чисел: 1) 48 и 36. Решение:
- 23. Примеры. Найти НОД чисел: 2) 28 и 15. 3)
- 24. Наименьшее натуральное число, которое делится на каждое из данных натуральных чисел а, b, … называется наименьшим
- 25. Упражнения Разложить на простые множители числа: 6, 18, 36, 49, 150, 1024, 2250, 9555. Найти НОД
- 27. Скачать презентацию























 Решение задач
Решение задач Графические диктанты, все классы
Графические диктанты, все классы Инвариант. Решение олимпиадных задач
Инвариант. Решение олимпиадных задач Деление десятичных дробей
Деление десятичных дробей Легенды о Пифагоре и его теореме
Легенды о Пифагоре и его теореме Тренажер Считаем с Колобком
Тренажер Считаем с Колобком Векторы в пространстве
Векторы в пространстве Пространство
Пространство Параллелограмм. Свойства параллелограмма. Трапеция
Параллелограмм. Свойства параллелограмма. Трапеция В четырех углах или Путешествие в семью параллелограммов
В четырех углах или Путешествие в семью параллелограммов Понятие объема. Объем
Понятие объема. Объем Прямоугольный треугольник
Прямоугольный треугольник 08_ ОТС_ Основы теории СП-2
08_ ОТС_ Основы теории СП-2 Окружность и круг
Окружность и круг Викторина по геометрии
Викторина по геометрии Шар. Сфера
Шар. Сфера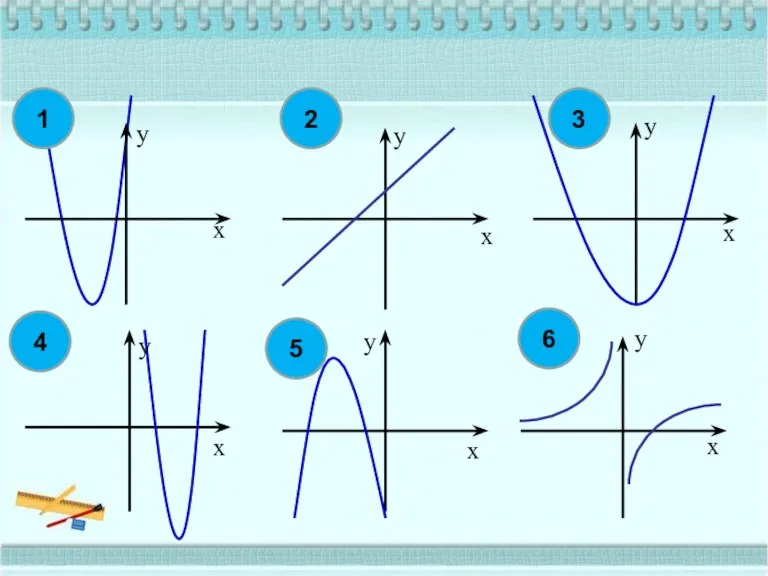 Квадратная функция и ее график
Квадратная функция и ее график Перпендикулярные прямые
Перпендикулярные прямые Теория погрешностей
Теория погрешностей Измерения. Старинные и современные меры величин
Измерения. Старинные и современные меры величин Подобные треугольники
Подобные треугольники Вычисление неопределенного интеграла
Вычисление неопределенного интеграла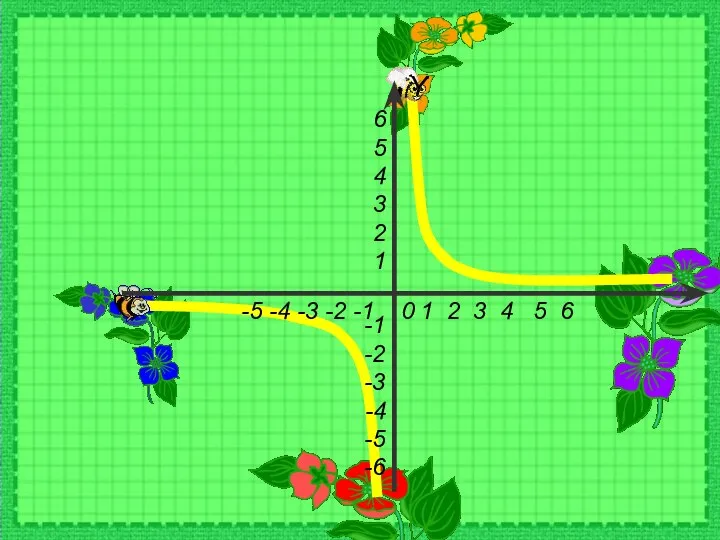 Функция у=1/х и её график
Функция у=1/х и её график Презентация на тему Сфера и шар
Презентация на тему Сфера и шар  Цилиндр. Круговой цилиндр
Цилиндр. Круговой цилиндр Вычитание чисел. Математический тренажер
Вычитание чисел. Математический тренажер Счет до 1000
Счет до 1000 Диаграмма. Виды диаграмм
Диаграмма. Виды диаграмм