Содержание
- 2. Евдокс Книдский ок. 408 — ок. 355 год до н. э. Интегральное исчисление появилось во времена
- 3. Лейбниц Готфрид Вильгельм (1646-1716) Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы
- 4. Готфрид Вильгельм Лейбниц (1646—1716) Исаак Ньютон (1643 – 1727) Ньютон и Лейбниц открыли независимо друг от
- 5. Огюстен Луи Коши (1789 – 1857) Карл Теодор Вильгельм Вейерштрасс (1815 1897 ) Работы Коши и
- 6. В развитии интегрального исчисления приняли участие русские математики: М.В. Остроградский (1801 – 1862) В.Я. Буняковский (1804
- 7. Первообразная. Задача дифференциального исчисления: по данной функции найти её производную. Задача интегрального исчисления: найти функцию, зная
- 8. Пример 1. Найти первообразные для функций:
- 9. Для всякой ли функции f(x) существует первообразная? Теорема. Если функция непрерывна на каком- нибудь промежутке, то
- 10. Найти первообразную для функции f(x)=4x3. Т.о. функция f(x)=4x3, х∈R имеет бесконечное множество первообразных.
- 11. Теорема. Если функция F(x) является первообразной для функции f(x) на некотором промежутке, то множество всех первообразных
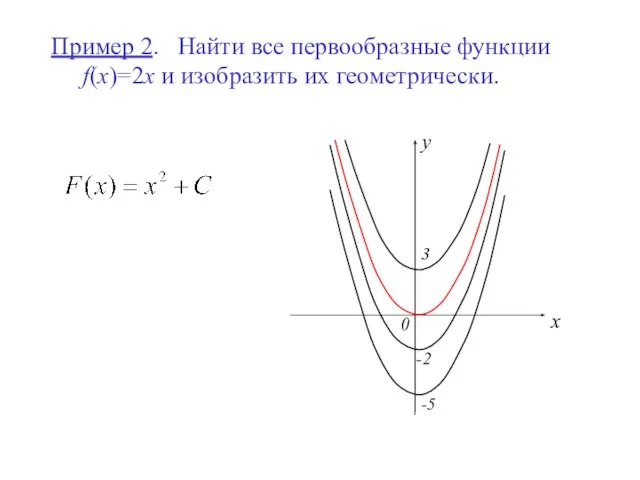
- 12. Пример 2. Найти все первообразные функции f(x)=2x и изобразить их геометрически. y x 0 -2 3
- 13. Неопределённый интеграл. Множество всех первообразных F(x)+C функции f(x) на некотором промежутке называется неопределённым интегралом и обозначается
- 14. - подынтегральная функция - подынтегральное выражение - знак неопределённого интеграла х – переменная интегрирования F(x)+C –
- 15. Свойства неопределённого интеграла. 10. Дифференциал от неопределённого интеграла равен подынтегральному выражению, а производная неопределённого интеграла равна
- 16. 20. Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная, т.е 30. Неопределённый
- 17. Таблица интегралов. В частности: В частности:
- 18. В частности: В частности:
- 19. Основные методы интегрирования. Метод непосредственного интегрирования. Непосредственным интегрированием называется такой метод вычисления интегралов, при котором они
- 20. Вычисление интегралов с помощью преобразования подынтегрального выражения к табличной форме и использования свойств неопределенного интеграла называется
- 21. Пример. Используя таблицу и свойства интегралов, найти интегралы.
- 23. Пример 7. Вычислить интеграл
- 24. Пример 8. Вычислить интеграл
- 25. Пример 9. Вычислить интеграл
- 26. Пример 10. Вычислить интеграл
- 27. Пример 11. Вычислить интеграл
- 28. Пример 12. Вычислить интеграл
- 29. Пример 13. Вычислить интеграл
- 30. Пример 14. Вычислить интеграл
- 31. Пример 15. Вычислить интеграл
- 33. Скачать презентацию



















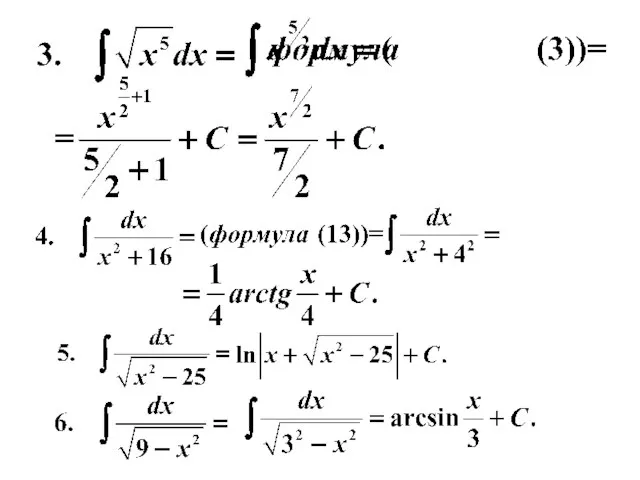









 Треугольники
Треугольники Презентация на тему Наглядная геометрия для начальной школы
Презентация на тему Наглядная геометрия для начальной школы  Презентация на тему Сравнение углов
Презентация на тему Сравнение углов  Числа и точки на прямой
Числа и точки на прямой Презентация на тему Свойства четырехугольников
Презентация на тему Свойства четырехугольников  Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Вписанная окружность в треугольник
Вписанная окружность в треугольник Производная и интеграл степенной функции с действительным показателем
Производная и интеграл степенной функции с действительным показателем Объем шара и площадь сферы
Объем шара и площадь сферы Несложная тригонометрия
Несложная тригонометрия Деление дробей. Путешествие в Китай. 5 класс
Деление дробей. Путешествие в Китай. 5 класс Первый признак подобия треугольников
Первый признак подобия треугольников Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Происхождение неевклидовой геометрии
Происхождение неевклидовой геометрии Тригонометрические таблицы
Тригонометрические таблицы Основные понятия теории множеств, комбинаторики, теории вероятности
Основные понятия теории множеств, комбинаторики, теории вероятности Современная финансовая математика
Современная финансовая математика Признаки равнобедренного треугольника
Признаки равнобедренного треугольника Презентация на тему Усеченный конус
Презентация на тему Усеченный конус  Высота. Длина. Площадь
Высота. Длина. Площадь Умножение десятичных дробей
Умножение десятичных дробей Дифференциальные уравнения
Дифференциальные уравнения Теорема о вписанном угле
Теорема о вписанном угле Подпространства. Проекции. Тема 9
Подпространства. Проекции. Тема 9 Задачи на готовых чертежах
Задачи на готовых чертежах Найди значение выражения. Реши задачу
Найди значение выражения. Реши задачу Комбинаторика
Комбинаторика Правильные многогранники
Правильные многогранники