Слайд 2Непрерывность функций.
Точки разрыва
Лекция

Слайд 3Непрерывность
Функция f(x), определенная на множестве Х,
называется непрерывной в точке ,

если
1)она определена в этой точке,
2) существует и
3)
Слайд 4 Равенство 3) можно также записать в виде:
Говорят: «если функция непрерывна

в точке x0 , то знак предела и функцию можно поменять местами».
Слайд 5Условие непрерывности
Существование равносильно тому,
что существуют равные друг другу левосторонний

и правосторонний пределы функции при , равные к тому же и значению функции в точке, то есть
Слайд 6Непрерывность на множестве
Говорят, что функция непрерывна на множестве Х, если она

непрерывна в каждой точке этого множества.
Слайд 7Пусть функция f(x) определена на промежутке [x0 ; x0 + δ) (на промежутке ( x0 –

δ; x0] ).
ОПРЕДЕЛЕНИЕ. Функция f(x) называется непрерывной в точке x0 справа (слева), если справедливо равенство
Очевидно, что f(x) непрерывна в точке x0 ⇔ f(x) непрерывна в точке x0 справа и слева.
ОПРЕДЕЛЕНИЕ. Функция f(x) называется непрерывной на интервале (a; b) если она непрерывна в каждой точке этого интервала.
Функция f(x) называется непрерывной на отрезке [a; b] если она непрерывна на интервале (a; b) и имеет одностороннюю непрерывность в граничных точках (т.е. непрерывна в точке a справа, в точке b – слева).
Слайд 8 Непрерывность
Теперь переформулируем определение непрерывности в других терминах. Обозначим
и

назовем его приращением аргумента в точке ,
будем называть приращением функции в точке .
Слайд 9 Непрерывность
Теорема. Функция непрерывна в точке тогда и только тогда, когда

бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке, то есть если
Задание. Используя эту теорему, исследовать на непрерывность функцию y=sinx.
Слайд 10Теоремы о непрерывных функциях
Теорема.
Пусть заданные на одном и том же

множестве Х функции и непрерывны в точке . Тогда функции
, ,
непрерывны в точке ,если знаменатель не равен нулю в этой точке:
.
Слайд 11Теоремы о непрерывных функциях
Теорема (о непрерывности сложной функции). Пусть функция
непрерывна

в точке , а функция непрерывна в точке .
Тогда сложная функция
непрерывна в точке .
Теоремы о непрерывных функциях следуют из свойств пределов функций.
Слайд 12Непрерывность элементарных функций
Всевозможные арифметические комбинации простейших элементарных функций, которые рассматривают в

школьном курсе алгебры и начал анализа, мы будем называть элементарными функциями. Например,
является элементарной.
Все элементарные функции непрерывны в области определения
Слайд 13Разрывы функций
Дадим теперь классификацию точек разрыва функций. Возможны следующие случаи.
1.Если

существуют и
конечны, но не равны друг другу, то точку называют точкой разрыва первого рода. При
этом величину называют
скачком функции в точке .
Если односторонние пределы совпадают, то точка разрыва первого рода называется точкой устранимого разрыва (см. ниже)
Слайд 14Пример
Исследовать на непрерывность функцию
Эта функция может претерпевать разрыв только в точке

0, где происходит переход от одного аналитического выражения к другому, а в остальных точках области определения функция непрерывна.
Слайд 15Пример
Из условия непрерывности следует:
Таким образом, в точке 0 функция претерпевает разрыв

1-го рода со скачком 1.
Слайд 16График функции
На рисунке изображена функция, имеющая разрыв 1-го рода в начале

координат.
Слайд 17Разрывы функций
2.Если в точке , но в точке функция либо не

определена, либо
, то эта точка разрыва первого рода является точкой устранимого разрыва. Последнее объясняется тем, что если в этом случае доопределить или видоизменить функцию , положив ,
то получится непрерывная в точке функция.
Слайд 18Разрывы функций
3. Точка разрыва функции, не являющаяся точкой разрыва первого рода,

в частности, точкой устранимого разрыва, является точкой разрыва второго рода.
Очевидно, что точки разрыва второго рода - это точки, в которых хотя бы один из односторонних пределов не существует, например, функция стремится к бесконечности справа или слева. Например, в точке х=1 имеет разрыв 2-го рода.
Слайд 19Пример
Исследуем функцию . Как элементарная функция она всюду непрерывна, кроме точки

х=1.
,
Имеем разрыв 2-го рода с бесконечным скачком.
(запись в вычислениях с точки зрения математики не совсем верная, но позволяет лучше понять смысл)
Слайд 20Св Свойства функций, непрерывных на отрезке ойства непрерывных на отрезке функций
Первая

теорема Больцано-Коши об обращении функции в нуль. Пусть функция определена и непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения различных знаков, т. е.
Тогда существует точка
такая, что
Слайд 21Свойства непрерывных на отрезке ф Свойства функций, непрерывных на отрезке ункций
Проиллюстрируем
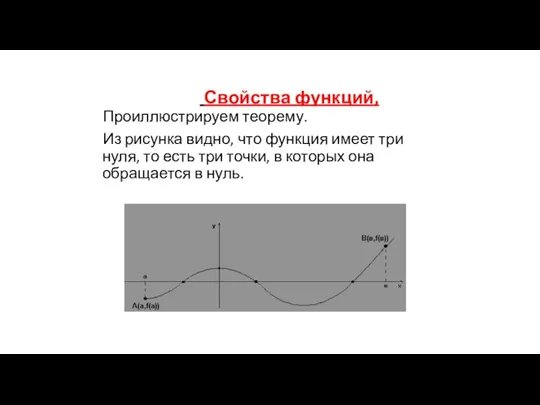
теорему.
Из рисунка видно, что функция имеет три нуля, то есть три точки, в которых она обращается в нуль.
Слайд 22Свойства непрерывных на отрезке фу Свойства функций, непрерывных на отрезке нкций
Вторая

теорема Больцано-Коши о промежуточном значении функции. Пусть функция определена и непрерывна на отрезке [a, b] и на концах этого отрезка принимает неравные значения . Тогда, каково бы ни было число между числами , найдется точка такая, что
.
Слайд 23 Свойства функций, непрерывных на отрезке
Теорема Вейерштрасса
Пусть функция f(x) непрерывна на

отрезке [a; b] . Тогда
1) f(x) – ограничена на [a; b] ;
2) f(x) принимает на [a; b] свое наибольшее и наименьшее значения.
ОПРЕДЕЛЕНИЕ.
Значение функции m = f(x1) называется наименьшим, если
m ≤ f(x), ∀x∈D(f).
Значение функции M = f(x2) называется наибольшим, если
M ≥ f(x), ∀x∈D(f).
Замечание. Наименьшее (наибольшее) значение функция может принимать в нескольких точках отрезка.






















 Геометрия, 10 класс
Геометрия, 10 класс Параллельные алгоритмы вычислительной алгебры. Распараллеливание на компьютерах с распределенной памятью
Параллельные алгоритмы вычислительной алгебры. Распараллеливание на компьютерах с распределенной памятью 1665470218901_Лекция Бернулли-1
1665470218901_Лекция Бернулли-1 Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами
Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами Задачи на нахождение элементов призмы
Задачи на нахождение элементов призмы Сложение однозначных чисел с переходом через десяток вида * + 6
Сложение однозначных чисел с переходом через десяток вида * + 6 Треугольник. Свойства прямоугольного треугольника
Треугольник. Свойства прямоугольного треугольника Площадь многоугольников
Площадь многоугольников Презентация на тему Космическое путешествие 1 класс
Презентация на тему Космическое путешествие 1 класс  Комбинаторная задача с лампочками
Комбинаторная задача с лампочками Математическая интеллектуальная игра для всей семьи
Математическая интеллектуальная игра для всей семьи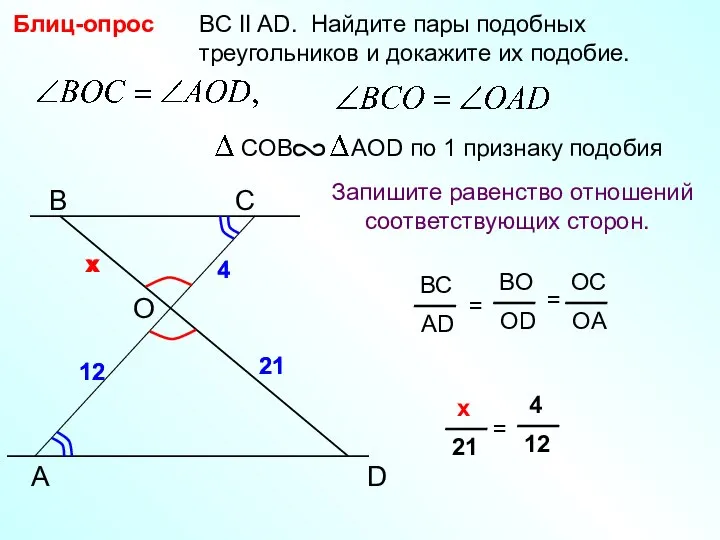 Признаки подобия треугольников
Признаки подобия треугольников Веселая математика!
Веселая математика! О треугольниках
О треугольниках Методы решения системы трёх линейных уравнений с тремя неизвестными
Методы решения системы трёх линейных уравнений с тремя неизвестными Презентация на тему Деловая игра по математике
Презентация на тему Деловая игра по математике  Презентация на тему Комбинаторные задачи (5 класс)
Презентация на тему Комбинаторные задачи (5 класс)  Тригонометрические уравнения
Тригонометрические уравнения Формулы сокращённого умножения
Формулы сокращённого умножения Длина окружности
Длина окружности Пирамида
Пирамида Понятие логарифма
Понятие логарифма Співвідношення між тригонометричними функціями
Співвідношення між тригонометричними функціями Задачи на пропорцию
Задачи на пропорцию Подготовка к ЕГЭ по математике
Подготовка к ЕГЭ по математике Задания по таблицам
Задания по таблицам Выражение отношения в процентах
Выражение отношения в процентах Числовая окружность. Занятие 1-2
Числовая окружность. Занятие 1-2